洛谷:集合与差分
1.学籍管理(map)
#include
#include 这道题要让我们存储学籍信息,一个学号对应一个成绩,很容易想到要用map来存储数据,之后根据题目要求一步步模拟就行了。(要用到count函数,erase函数,size函数)
2.保龄球(map)
#include
#include 这道题让我们存储每个位置有几个球便于之后的查询,一个位置对应一个保龄球的数量,也是要用map来做,牛逼的是我们可以把保龄球的数量当作关键字来存储,对应的位置作为值,这样访问的时候,可以直接保龄球的数量来找到对应的位置,牛逼!
3.Cities and States S(map)
#include
#include 这道题也是要根据城市来找对应洲,两个数据,也可以用map,string是城市和洲的名称的合写,int来判断是否出现过。很显然我们只需要城市的前两个字符就可以,我们使用substr函数来分割字符,如果城市的名称和洲的名称不一样,再执行之后的操作,如果m[a+b]是0,说明之前没有出现,ans+=0;是1代表之前出现过,那就构成了一对,ans+=1;因为是反着来的,所以之后我们要对m[b+a]++。
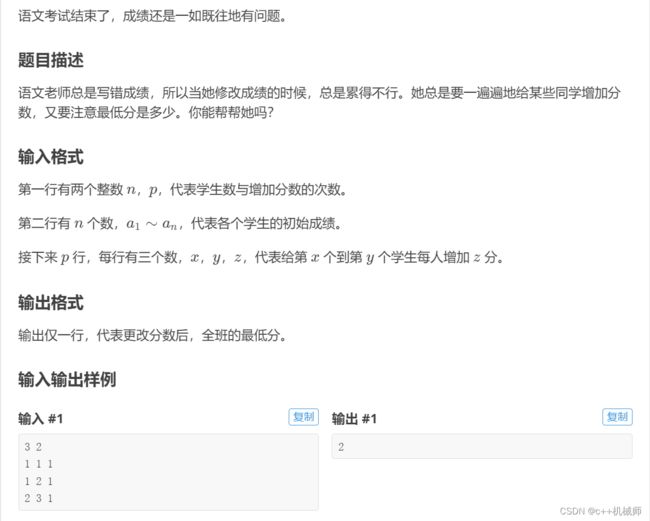
4.语文成绩(一维差分)
#include
using namespace std;
int n,p,a,x,y,z;
int ming=1e9;
int grade[5000001];//差分易于在O(1)内维护区间内所有的数加减乘除一个值
int d[5000001];
int main()
{
cin>>n>>p;
for(int i=1;i<=n;i++)
{
cin>>grade[i];
}
for(int i=1;i<=n;i++)
{
d[i]=grade[i]-grade[i-1];
}
for(int i=1;i<=p;i++)
{
cin>>x>>y>>z;
d[x]+=z;
d[y+1]-=z;
}
for(int i=1;i<=n;i++)
{
grade[i]=d[i]+grade[i-1];
ming=min(ming,grade[i]);
}
cout< 这道题我们要对一个区间整体加上一个数,这种事就要交给差分来做,差分就是比较容易在O(1)时间内维护区间内所有的数加减乘除一个数,我们先构造差分数组,因为d[i]=a[i]-a[i-1],所以我们对差分数组加上一个数,也会对原数组每个元素加上一个数,但由于区间外的不能改变,所以我们对区间外再减去一个数,最后恢复原数组1即可。
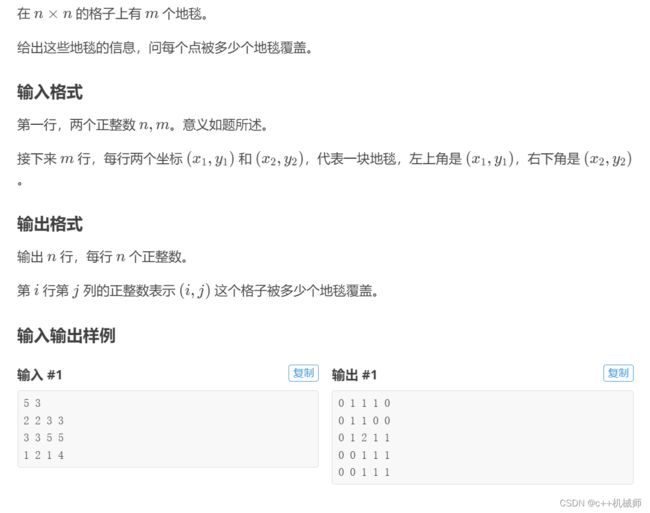
5.地毯(二维差分)
#include
#include
using namespace std;
int a[1002][1002], b[1002][1002];
int n,m,x1,y1,x2,y2;
void insert(int x1, int y1, int x2, int y2,int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
insert(i, j, i, j, a[i][j]); //构建差分数组
}
}
while (m--)
{
cin >> x1 >> y1 >> x2 >> y2;
insert(x1, y1, x2, y2,1);
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; //二维前缀和
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
printf("%d ", b[i][j]);
}
printf("\n");
}
return 0;
}
这道题要对一个矩形区域内的加上一个数,就是差分二维化,要注意的是最后恢复原数组时,因为原数组是差分数组的前缀和,所以差分数组相加等于原数组,我们直接对差分数组进行操作就可以。