PSNR SSIM UCIQE UIQM评价指标说明与Python实现

1. 峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)

​ 峰值信噪比（PSNR）是一个表示信号最大可能功率和影响它的表示精度的破坏性噪声功率比值的工程术语。由于许多信号都有非常宽的动态范围，峰值信噪比常用对数分贝dB单位来表示。

给定一个大小为$M\times N\times C$的干净图像$I$和噪声图像$K$，均方误差(MSE)定义为：
$$MSE=\frac{1}{MNC}\sum _{i=0}^{M-1}\sum _{j=0}^{N-1}\sum _{k=0}^{C-1}[I(i,j,k)-K(i,j,k){]}^2\text{\hspace{1em}(1.1)}$$
然后PSNR(dB)定义为：
$$PSNR=10\cdot lo{g}_{10}(\frac{MA{X}_I^2}{MSE})=20\cdot lo{g}_{10}(\frac{MA{X}_I}{MSE})\text{\hspace{1em}(1.2)}$$
其中$MA{X}_I^2$为图片可能的最大像素值，如果每个像素都由8位二进制表示，那么就为255。通常，如果像素值由B位二进制来表示，那么$MA{X}_I=2^B-1$。一般地，针对uint8数据，最大像素值为255；针对浮点型数据，最大像素值位1。最大像素值具体是多少取决于前面是否对图像进行了归一化，在读入图像时，默认时0-255整数型，如果没有归一化后面最大像素值就为255，否则为1。具体实现代码：

import numpy as np
from skimage.metrics import structural_similarity as compare_ssim
from skimage.metrics import peak_signal_noise_ratio as compare_psnr
import math
import cv2

def img_loader(path):
    img = cv2.imread(path)
    return img

def psnr1(image_true, image_test):
    '''image_true: ground_truth图像
       image_test: 恢复后的图像
       psnr1和psnr2 区别在于求mse的时候是否进行255归一化,如果先对图像进行归一化,那么后面MAX=1, 否则为255
    '''
    mse = np.mean((image_true/1.0-image_test/1.0)**2)
    #compute psnr
    if mse < 1e-10:
        return 100
    psnr = 20*math.log10(255/math.sqrt(mse))
    return psnr

def psnr2(image_true, image_test):
    '''image_true: ground_truth图像
       image_test: 恢复后的图像
       psnr1和psnr2 区别在于求mse的时候是否进行255归一化,如果先对图像进行归一化,那么后面MAX=1, 否则为255
    '''
    mse = np.mean((image_true/255.0-image_test/255.0)**2)
    #compute psnr
    if mse < 1e-10:
        return 100
    psnr = 20*math.log10(1/math.sqrt(mse))
    return psnr   

if __name__ =="__main__":
    path_input = './test_img/860_img_.png'
    path_result = './results/results_2842/860_img_corrected.png'
    input = img_loader(path_input)
    result = img_loader(path_result)
    my_psnr1 = psnr1(input, result)
    my_psnr2 = psnr2(input, result)
    skimage_psnr = compare_psnr(input, result)
    print("psnr1={}, psnr2={}, skimage={}".format(my_psnr1, my_psnr2, skimage_psnr))

输出结果对比：

所以MSE越小，则PSNR越大；PSNR越大，代表着图像质量越好。一般来说：

• PSNR高于40dB说明图像质量极好（即非常接近原始图像）；
• 在30—40dB通常表示图像质量是好的（即失真可以察觉但可以接受）；
• 在20—30dB说明图像质量差；
• PSNR低于20dB图像不可接受；

2. 结构相似度(Structural Similarity，SSIM)

​ SSIM（structural similarity）结构相似度是一种全参考的图像质量评价指标，它分别从亮度、对比度、结构三方面度量两幅图像相似性，其值越大越好，最大为1；作为结构相似性理论的实现，结构相似度指数从图像组成的角度将结构信息定义为独立于亮度、对比度的，反映场景中物体结构的属性，并将失真建模为亮度、对比度和结构三个不同因素的组合；用均值作为亮度的估计，标准差作为对比度的估计，协方差作为结构相似程度的度量。由-1表示不相似到1表示完全相同。

​ 传统检测图像质量的方法MSE,PSNR与人眼的实际视觉感知是不一致的，SSIM算法在设计上考虑了人眼的视觉特性，比传统方式更符合人眼视觉感知，MSE或者是PSNR算法，都是对绝对误差的评估，SSIM是一种基于感知的计算模型，它能够考虑到图像的结构信息在人的感知上的模糊变化，该模型还引入了一些与感知上的变化有关的感知现象，包含亮度mask和对比mask，结构信息指的是像素之间有着内部的依赖性，尤其是空间上靠近的像素点。这些依赖性携带着目标对象视觉感知上的重要信息。SSIM具体公式：
$$SSIM=\frac{(2{\mu }_x{\mu }_y+C1)(2{\sigma }_{xy}+C2)}{({\mu }_x^2+{\mu }_y^2+C1)({\sigma }_x^2+{\sigma }_y^2+C2)}\text{\hspace{1em}(2.1)}$$
其中${\mu }_x,{\mu }_y$指的是两幅图像的平均值值，用来刻画两幅图像亮度的一致性，${\mu }_x=\frac{1}{N}{\sum }_{i=1}^N{x}_i$，$x_i$为图像$x$的第$i$个像素值，$N$为像素值总数。${\sigma }_x,{\sigma }_y$代表两幅图像像素值的标准差，表示两幅图像对比度一致性，${\sigma }_x=\sqrt{\frac{1}{N-1}{\sum }_{i=1}^N(x_i-u_x{)}^2}$，${\mu }_x$为图像的均值，${\sigma }_{xy}=\frac{1}{N-1}{\sum }_{i=1}^N(x_i-{\mu }_x)(y_i-{\mu }_y)$表示两幅图像的协方差矩阵，$C_1,C_2$为防止除0的常量值。

​ 上述是简化后的公式，具体如前面提到，SSIM将两幅图像的比较建模为亮度、对比度和结构三个不同因素的组合，在SSIM中有3个比较函数，用来对比两幅图像在亮度、对比度和结构上的差异。

亮度比较函数

​ 由函数$l(x,y)$定义，一幅图有 $N $个像素点，每个像素点的像素值为 $x_i$，那么该图像的平均亮度为，具体公式如下所示：
$$l(x,y)=\frac{2{\mu }_x{\mu }_y+C_1}{{\mu }_x^2+{\mu }_y^2+C1}\text{\hspace{1em}(2.2)}$$
其中$\mu$表示图像的均值，$x$和$y$表示被比较的两个图像，$C_1$为常熟，保证分母不为0，$C_1=(K_{1}L{)}^2$，通常$K_1=0.01$，$L$是灰度值的动态范围，一般为$2^8-1=255$。当$x=y$ 时, $l(x,y)=1$。

对比度比较函数

​ 由函数$c(x,y)$定义，就是图像明暗的变化剧烈程度，也就是像素值的标准差。具体公式如下所示：
$$c(x,y)=\frac{2{\sigma }_x{\sigma }_y+C_2}{{\sigma }_x^2+{\sigma }_y^2+C_2}\text{\hspace{1em}(2.3)}$$
其中$\sigma$表示图像的标准差，$x$和$y$表示两个比较的图像。$C_2=(K_{2}L{)}^2$，与$C_1$作用一致，通常$K_2=0.03$,当$x=y$ 时， $c(x,y)=1$。

结构比较函数

​ 由函数$s(x,y)$定义，需要注意的是，对一幅图而言，其亮度和对比度都是标量，而其结构显然无法用一个标量表示，而是应该用该图所有像素组成的向量来表示。同时，研究结构相似度时，应该排除亮度和对比度的影响，即排除均值和标准差的影响。归根结底，最终研究的是归一化的两个向量**$\frac{x-{\mu }_x}{{\sigma }_x}和\frac{y-{\mu }_y}{{\sigma }_y}$**之间的关系，根据均值与标准差的关系，可知这两个向量的模长均为$\sqrt{N-1}$（通常样本的标准差是由${\sigma }^2=\frac{\sum (x-u{)}^2}{N-1}$得到，所以上式$\frac{x-\mu }{\sigma }$的模为$\sqrt{N-1}$），因此它们的余弦相似度为:
$$\begin{gathered} s(x,y)=(\frac{1}{\sqrt{N-1}}\frac{x-{\mu }_x}{{\sigma }_x})(\frac{1}{\sqrt{N-1}}\frac{y-{\mu }_y}{{\sigma }_y}) \\ =\frac{1}{{\sigma }_x{\sigma }_y}(\frac{1}{N-1}\sum _{i=1}^N(x_i-{\mu }_x)(y_i-{\mu }_y))\text{\hspace{1em}(2.4)} \end{gathered}$$
其中${\sigma }_{xy}=\frac{1}{N-1}{\sum }_{i=1}^N(x_i-{\mu }_x)(y_i-{\mu }_y)$。

具体公式如下所示：
$$s(x,y)=\frac{{\sigma }_{xy}+C_3}{{\sigma }_x{\sigma }_y+C_3}$$
其中${\sigma }_{xy}$表示比较图像$x$和$y$之间的协方差。

最终定义SSIM为：
$$SSIM(x,y)=[l(x,y){]}^a\cdot [c(x,y){]}^{\beta }\cdot [s(x,y){]}^{\gamma }\text{\hspace{1em}(2.5)}$$
其中$a>0,\beta >0,\gamma >0$表示每个度量标准的相对重要性。SSIM的公式遵循以下三个原则：

1. 对称性，$S(x,y)=S(y,x)$;
2. 有界性，$S(x,y)\le 1$；
3. 极值唯一性，$S(x,y)=1$ ,仅当$x=y$ 时。

为了简化，SSIM最终表达式为：
$$SSIM=\frac{(2{\mu }_x{\mu }_y+C1)(2{\sigma }_{xy}+C2)}{({\mu }_x^2+{\mu }_y^2+C1)({\sigma }_x^2+{\sigma }_y^2+C2)}\text{\hspace{1em}(2.1)}$$
上面的 SSIM 不能用于一整幅图。因为在整幅图的跨度上，均值和方差往往变化剧烈；同时，图像上不同区块的失真程度也有可能不同，不能一概而论；此外类比人眼睛每次只能聚焦于一处的特点。作者采用 sliding window （这里可以看做卷积）以步长为 1 计算两幅图各个对应 sliding window 下的 patch 的 SSIM，然后取平均值作为两幅图整体的 SSIM，称为 Mean SSIM。简写为 MSSIM（注意和后续出现的 multi-scale SSIM：MS-SSIM 作区分）
如果像素$x_i$对应的高斯核权重为 $w_i$。那么加权均值，方差，协方差的公式为：
$${\mu }_x=\sum _{i=1}^N{w}_i{x}_i$$

$${\sigma }_x=\sqrt{(\sum _{i=1}^N{w}_i(x_i-u_x{)}^2)}$$

$${\sigma }_{xy}=\sum _{i=1}^N{w}_i(x_i-{\mu }_x)(y_i-{\mu }_y)$$

假如整幅图有M个 patch，那么 MSSIM 公式为：
$$MSSIM=(x,y)=\frac{1}{M}\sum _{j=1}^{M}SSIM(x_j,y_j)$$

$$\begin{gathered} {\sigma }_x^2=\sum _{i=1}^N{w}_i(x_i-{\mu }_x{)}^2 \\ =\sum _{i=1}^N{w}_i(x_i^2-2x_i{\mu }_x+{\mu }_x^2) \\ =\sum _{i=1}^N{w}_i{x}_i^2-2{\mu }_x\sum _{i=1}^N{w}_i{x}_i+{\mu }_x^2\sum _{i=1}^N{w}_i \\ =E[x^2]-2{\mu }_x^2+u_x^2 \\ =E[x^2]-E^2[x] \end{gathered}$$

求图像的方差，只需做两次卷积，一次是对原图卷积，一次是对原图的平方卷积，然后用后者减去前者的平方即可。
$$\begin{gathered} {\sigma }_{xy}^2=E[(x-{\mu }_x)(y-{\mu }_y)] \\ =\sum _{i=1}^N(x_i-{\mu }_x)(y_i-{\mu }_y) \\ =\sum _{i=1}^N{w}_i(x_i{y}_i-x_i{\mu }_y-{\mu }_x{y}_i+{\mu }_x{\mu }_y) \\ =\sum _{i=1}^N{w}_i(x_i{y}_i)-{\mu }_y\sum _{i=1}^N{w}_i{x}_i-{\mu }_x\sum _{i=1}^N{w}_i{y}_i+{\mu }_x{\mu }_y\sum _{i=1}^N{w}_i) \\ =E[xy]-2{\mu }_x{\mu }_y+{\mu }_x{\mu }_y \\ =E[xy]-E[x]E[y] \end{gathered}$$
求两图的协方差，只需做三次卷积，第一次是对两图的乘积卷积，第二次和第三次分别对两图本身卷积，然后用第一次的卷积结果减去第二、三次卷积结果的乘积。

代码实现:

import numpy as np
from skimage.metrics import structural_similarity as compare_ssim
from skimage.metrics import peak_signal_noise_ratio as compare_psnr
import math
import cv2

def img_loader(path):
    img = cv2.imread(path)
    return img

def ssim(img1, img2):
    C1 = (0.01 * 255)**2
    C2 = (0.03 * 255)**2
    img1 = img1.astype(np.float64)
    img2 = img2.astype(np.float64)
    # 定义高斯核
    kernel = cv2.getGaussianKernel(11, 1.5)
    window = np.outer(kernel, kernel.transpose())
    # 利用高斯核求局部均值
    mu1 = cv2.filter2D(img1, -1, window)[5:-5, 5:-5] # valid
    mu2 = cv2.filter2D(img2, -1, window)[5:-5, 5:-5]
    # 均值的平方
    mu1_sq = mu1**2
    mu2_sq = mu2**2
    mu1_mu2 = mu1 * mu2
    # 图像的方差，做两次卷积，一次是对原图卷积，一次是对原图的平方卷积，然后用后者减去前者的平方
    sigma1_sq = cv2.filter2D(img1**2, -1, window)[5:-5, 5:-5] - mu1_sq
    sigma2_sq = cv2.filter2D(img2**2, -1, window)[5:-5, 5:-5] - mu2_sq
    # 两图的协方差，做三次卷积，第一次是对两图的乘积卷积，第二次和第三次分别对两图本身卷积，
    # 然后用第一次的卷积结果减去第二、三次卷积结果的乘积。
    sigma12 = cv2.filter2D(img1 * img2, -1, window)[5:-5, 5:-5] - mu1_mu2
    ssim_map = ((2 * mu1_mu2 + C1) * (2 * sigma12 + C2)) / ((mu1_sq + mu2_sq + C1) *
                                (sigma1_sq + sigma2_sq + C2))
    return ssim_map.mean()

def calculate_ssim(img1, img2):
    '''calculate SSIM
    the same outputs as MATLAB's
    img1, img2: [0, 255]
    '''
    if not img1.shape == img2.shape:
        raise ValueError('Input images must have the same dimensions.')
    if img1.ndim == 2:
        return ssim(img1, img2)
    elif img1.ndim == 3:
        if img1.shape[2] == 3:
            ssims = []
            for i in range(3):
                ssims.append(ssim(img1, img2))
            return np.array(ssims).mean()
        elif img1.shape[2] == 1:
            return ssim(np.squeeze(img1), np.squeeze(img2))
    else:
        raise ValueError('Wrong input image dimensions.')

if __name__ =="__main__":
    path_input = './test_img/860_img_.png'
    path_result = './results/results_2842/860_img_corrected.png'
    input = img_loader(path_input)
    result = img_loader(path_result)
    ssim1 = calculate_ssim(input, result)
    ssim2 = compare_ssim(input, result, channel_axis=-1)
    print("ssim1={}, ssim2={}".format(ssim1, ssim2))

最终结果，手动实现与调用函数计算结果稍有不一致：

3. 水下图像质量评估(Underwater Image Quality Measurement, UIQM)

​ UIQM是一种基于人眼视觉系统的无参考水下图像质量评价指标，其针对水下图像的退化机理与成像特点，采用色彩测量指标（UICM），清晰度测量指标（UISM），对比度测量指标（UIConM）作为评价依据，将UIQM表示为三者的线性组合。**其值越大，表示图像的颜色平衡、清晰度、对比度越佳。**具体公式为:
$$UIQM=c_1\times UICM+c_2\times UISM+c_{3}UIConM\text{\hspace{1em}(3.1)}$$

色彩测量指标(Underwater Image Colorfulness Measure, UICM)

​ 许多水下图像都存在严重的色彩损失问题。随着水的深度增加，不同波长的颜色会逐渐衰减。红色最先消失，因为红色的波长最短。所以，水下图像通常呈现出蓝色或绿色。此外，有限的照明条件也会导致水下图像出现严重的色彩稀释情况。一个好的水下图像增强算法应该产生良好的色彩再现性。HVS能够获得对立色彩空间中的颜色。因此，在UICM中使用了与色度RG和YB相关的两个对立颜色分量，具体如下：
$$RG=R-GYB=\frac{(R+G)}{2}-B$$
水下图像通常有很严重的噪声干扰。以下需要对RG和YB两个分量分别计算， 以下公式以计算RG为例。在测量水下图像色彩度时，不使用常规统计值，而是使用非对称alpha截断统计值。在该截断统计值下均值的定义为:
$${\mu }_{a,RG}=\frac{1}{K-T_{aL}-T_{aR}}\sum _{i=T_{aL}+1}^{K-T_{aR}}Intensit{y}_{RG,i}$$
其中$K=M\ast N$表示RG或者YB分量图像像素数，对RG或者YB像素按从小到大排序$x_1\le x_2...\le x_k$。令$T_{\alpha L}=\lceil \alpha L\times K\rceil$ (向上取整) $T_{\alpha R}=\lfloor \alpha R\times K\rfloor$(向下取整)为设定的取多少比例超参数，可以设置，通常为0.1。

二阶统计量方差${\sigma }^2$的定义如下：
$${\sigma }_{a,RG}^2=\frac{1}{N}\sum _{p=1}^N(Intensit{y}_{RG,p}-{\mu }_{a,RG}{)}^2$$
最终用于测量水下图像色彩度的总体色彩度公式为：
$$UICM=-0.0268\sqrt{{\mu }_{a,RG}^2+{\mu }_{a,YB}^2}+0.1586\sqrt{{\sigma }_{a,RG}^2+{\sigma }_{a,YB}^2}\text{\hspace{1em}(3.2)}$$
参考代码：

# 计算均值
def mu_a(x, alpha_L=0.1, alpha_R=0.1):
    """
      Calculates the asymetric alpha-trimmed mean
    """
    # 对输入部分像素值排序
    x = sorted(x)
    # get number of pixels
    K = len(x)
    # 获取截断的范围
    T_a_L = math.ceil(alpha_L*K)
    T_a_R = math.floor(alpha_R*K)
    # 计算公式权重
    weight = (1/(K-T_a_L-T_a_R))
    # 根据范围求和
    s   = int(T_a_L+1)
    e   = int(K-T_a_R)
    val = sum(x[s:e])
    val = weight*val
    # 返回均值
    return val
# 计算方差
def s_a(x, mu):
    val = 0
    for pixel in x:
        val += math.pow((pixel-mu), 2)
    return val/len(x)

def _uicm(x):
    # 将图像3个分量展开
    R = x[:,:,0].flatten()
    G = x[:,:,1].flatten()
    B = x[:,:,2].flatten()
    # 得到对应的RG和YB分量
    RG = R-G
    YB = ((R+G)/2)-B
    # 分别计算RG和YB分量的均值和方差
    mu_a_RG = mu_a(RG)
    mu_a_YB = mu_a(YB)
    s_a_RG = s_a(RG, mu_a_RG)
    s_a_YB = s_a(YB, mu_a_YB)
    # 根据公式得到最终的结果
    l = math.sqrt( (math.pow(mu_a_RG,2)+math.pow(mu_a_YB,2)) )
    r = math.sqrt(s_a_RG+s_a_YB)
    return (-0.0268*l)+(0.1586*r)

清晰度测量指标UISM

​ 清晰度是与保留细节和边缘有关的属性。对于在水下拍摄的图像，由于前向散射，会出现严重的模糊。这种模糊效果会导致图像清晰度下降。为了测量边缘的清晰度，首先对每个RGB颜色分量应用Sobel边缘检测器。然后将生成的边缘图与原始图像相乘得到灰度边缘图。通过上述方式，只将原始水下图像的边缘像素被保留下来。图像增强评价标准(enhancement measure estimation，EME)适用于具有均匀背景和非周期性图案的图像，用于测量边缘的锐度。EME的物理意思是对图像局部区域变化程度的表现，局部灰度变化越强，图像表现除的细节越强，得到的EME结果越大。 UISM的定义如下所示：
$$\begin{gathered} USIM=\sum _{c=1}^3{\lambda }_{c}EME(grayscaleedg{e}_c) \\ EME=\frac{2}{k_1{k}_2}\sum _{l=1}^{k_1}\sum _{k=1}^{k_2}log(\frac{I_{max,k.l}}{I_{min,k,l}}) \end{gathered}$$
在上面的方程中，图像被分为$k_1\times k_2$个块，每个块用$(I_{max},k,l)$和$(I_{min},k,l)$表示块区域中灰度最大的值与最小值，最终评价结果是每个小块区域中灰度最大值和最小值比值的对数均值。

参考代码:

def _uism(x):
    """
      Underwater Image Sharpness Measure
    """
    # 得到图像的每个颜色分量
    R = x[:,:,0]
    G = x[:,:,1]
    B = x[:,:,2]
    # 对每个分量使用sobel算子
    Rs = sobel(R)
    Gs = sobel(G)
    Bs = sobel(B)
    # 将生成的边缘图与原始图像相乘得到灰度边缘图
    R_edge_map = np.multiply(Rs, R)
    G_edge_map = np.multiply(Gs, G)
    B_edge_map = np.multiply(Bs, B)
    # 对每个通道使用EME算法
    r_eme = eme(R_edge_map, 10)
    g_eme = eme(G_edge_map, 10)
    b_eme = eme(B_edge_map, 10)
    # coefficients
    lambda_r = 0.299
    lambda_g = 0.587
    lambda_b = 0.144
    return (lambda_r*r_eme) + (lambda_g*g_eme) + (lambda_b*b_eme)

def eme(x, window_size):
    """
      Enhancement measure estimation
      x.shape[0] = height
      x.shape[1] = width
    """
    # 计算图像分块的数量
    k1 = x.shape[1]/window_size
    k2 = x.shape[0]/window_size
    # EME公式权重
    w = 2./(k1*k2)
    blocksize_x = window_size
    blocksize_y = window_size
    # 确保图像可以被window_size整除，可以把没法整除多余的像素切掉
    x = x[:blocksize_y*k2, :blocksize_x*k1]
    val = 0
    for l in range(k1):
        for k in range(k2):
            block = x[k*window_size:window_size*(k+1), l*window_size:window_size*(l+1)]
            # 求块区域中灰度最大的值与最小值
            max_ = np.max(block)
            min_ = np.min(block)
            # 合法性检查，避免计算log(0)
            if min_ == 0.0: val += 0
            elif max_ == 0.0: val += 0
            else: val += math.log(max_/min_)
    return w*val

对比度测量指标UIConM

​ UIConM是对水下图像中最亮和最暗部分的区分，通过增加图像的对比度，它可以增加明暗部分之间的分离，使阴影更暗，突出明亮的部分。降低图像的对比度意味着增加阴影。在水下图像中，对比度衰减是由后向散射引起的，我们可以通过在水下图像的较暗区域和较亮区域使用增量和减量来增强水下图像。在UIConM中，对比度是通过在强度图像上使用log AMEE度量来计算的:
$$UIConM=logAMEE(intensity)$$
其中$logAMEE$具体计算方式如下所示：
$$logAMEE=\frac{1}{k_1{k}_2}\sum _{l=1}^{k_1}\sum _{k=1}^{k_2}\frac{I_{max,k.l}-I_{min,k,l}}{I_{max,k.l}+I_{min,k,l}}log(\frac{I_{max,k.l}-I_{min,k,l}}{I_{max,k.l}+I_{min,k,l}})$$
在上式中，将图像分为$k_1\times k_2$块$(I_{max},k,l)$， $(I_{min},k,l)$表示各RGB颜色分量的近似对比度和EME度量。在此基础上，结合全像差测量方法，提出了一种新的水下图像质量测量方法。该方法是现有的和独立的图像测量技术的结合，它用于分析相当于人类观测的水下图像质量。在水下图像质量测量技术中，我们对水下图像进行了更加精确和增强的测量(图1)。整个评价标准流程如下图所示：

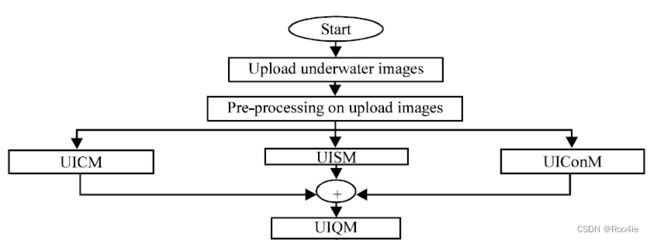
参考代码:

def _uiconm(x, window_size):
    """
      Underwater image contrast measure
      https://github.com/tkrahn108/UIQM/blob/master/src/uiconm.cpp
      https://ieeexplore.ieee.org/abstract/document/5609219
    """
    # 与EME算法一致，对图像分块
    k1 = x.shape[1]/window_size
    k2 = x.shape[0]/window_size
    # 计算权重
    w = -1./(k1*k2)
    blocksize_x = window_size
    blocksize_y = window_size
    # 确保图像可以被window_size整除，可以把没法整除多余的像素切掉
    x = x[:blocksize_y*k2, :blocksize_x*k1]
    # entropy scale - higher helps with randomness
    alpha = 1
    val = 0
    for l in range(k1):
        for k in range(k2):
            block = x[k*window_size:window_size*(k+1), l*window_size:window_size*(l+1), :]
            max_ = np.max(block)
            min_ = np.min(block)
            # 
            top = max_-min_
            bot = max_+min_
            if math.isnan(top) or math.isnan(bot) or bot == 0.0 or top == 0.0: val += 0.0
            else: val += alpha*math.pow((top/bot),alpha) * math.log(top/bot)
    return w*val

4. 水下彩色图像质量评估（UCIQE）

​ UCIQE是色彩浓度，饱和度和对比度的线性组合，用来定量评价水下图像非均于的色偏，模糊和低对比度的情况。属于没有参考（groundtruth）图像的图像质量评价指标，具体定义如下:
$$UCIQE=c_1\times {\sigma }_c+c_2\times co{n}_l+c_3\times {\mu }_s$$
式中，${\sigma }_c$为色度标准差，$co{n}_l$为亮度对比，${\mu }_s$为饱和度平均值，$c1、c2、c3$为加权系数。如上所述，对于感兴趣的水下彩色图像，色度方差与人类感知具有良好的相关性。采用色度差异来描述偏色还有其他原因。其中一个原因是，对于在人工照明的泥泞水中拍摄的彩色图像，后向散射是图像退化的主要来源，因为散射产生白色亮点，可能会严重影响图像处理方法的性能。基于对比度和梯度的通用指标将给出更高的分数。然而，色相分布不会受到后向散射的影响。图3(a)为在透明度为680cm的水中随相机距离增加而拍摄的水箱图像。相应的色相通道如图3(b)所示，色相直方图如图3©所示。从图3©的数据可以看出，随着相机距离的增加，色相的方差减小，尽管随着相机距离的增加，图像中的斑点也会增多。

图3 在680cm透明度水中人工照明和色调分布。(a) 色板距离相机分别为240cm、270cm、300cm、330cm和360cm。(b)相应的色相通道。(c)色相直方图

参考代码：

def getUCIQE(img):
    img_BGR = cv2.imread(img)
    img_LAB = cv2.cvtColor(img_BGR, cv2.COLOR_BGR2LAB) 
    img_LAB = np.array(img_LAB,dtype=np.float64)
    # 根据论文中给出的训练系数
    coe_Metric = [0.4680, 0.2745, 0.2576]
    
    img_lum = img_LAB[:,:,0]/255.0
    img_a = img_LAB[:,:,1]/255.0
    img_b = img_LAB[:,:,2]/255.0

    # 色度标准差
    chroma = np.sqrt(np.square(img_a)+np.square(img_b))
    sigma_c = np.std(chroma)

    # 亮度对比度
    img_lum = img_lum.flatten()
    sorted_index = np.argsort(img_lum)
    top_index = sorted_index[int(len(img_lum)*0.99)]
    bottom_index = sorted_index[int(len(img_lum)*0.01)]
    con_lum = img_lum[top_index] - img_lum[bottom_index]

    # 饱和度均值
    chroma = chroma.flatten()
    sat = np.divide(chroma, img_lum, out=np.zeros_like(chroma, dtype=np.float64), where=img_lum!=0)
    avg_sat = np.mean(sat)

    uciqe = sigma_c*coe_Metric[0] + con_lum*coe_Metric[1] + avg_sat*coe_Metric[2]
    return uciqe

参考链接:

https://blog.csdn.net/qq_35914625/article/details/113789903

https://ieeexplore.ieee.org/document/7305804

https://www.rcciit.org/students_projects/projects/it/2018/GR3.pdf

https://github.com/xahidbuffon/FUnIE-GAN/blob/master/Evaluation/uqim_utils.py

UCIQE-python/UCIQE.py at main · TongJiayan/UCIQE-python (github.com)