高精度(加减乘除幂次)
概念(是什么)
高精度算法(High Accuracy Algorithm)是处理大数字的数学计算方法,也被称作大整数计算,数字大小超过语言内建模型。
在一般的科学计算中,会经常算到小数点后几百位或者更多,当然也可能是几千亿几百亿的大数字。一般这类数字我们统称为高精度数,高精度算法是用计算机对于超大数据的一种模拟加,减,乘,除,乘方,阶乘,开方等运算。
目的(为什么)
C/C++中,经常会碰到限定数据范围的情况,当我们要进行很庞大的数字运算时(比如在进行某整数运算时连long long类型都容纳不下的时候)我们该怎么办?
高精度算法就为此而存在。
实现(怎么做)
对于非常庞大的数字无法在计算机中正常存储,于是,将这个数字拆开,拆成一位一位的,或者是四位四位的存储到一个数组中, 用一个数组去表示一个数字,这样这个数字就被称为是高精度数。高精度算法就是能处理高精度数各种运算的算法,但又因其特殊性,故从普通数的算法中分离,自成一家。
数据类型(所占字节,数量级等)
以64位系统为例:(1字节=8位)
int:四个字节,32位,范围-2^31~2^31-1,数量级为10^9
long long:八个字节,64位,范围-2^63~2^63-1,数量级为10^18
高精度加法
输入两个整数a,b,计算并输出它们的和。(0≤a,b≤10^500)
测评网址:https://www.luogu.com.cn/problem/P1601
显然long long也无法容纳这两个大数。(属高精度数)->运用高精度算法
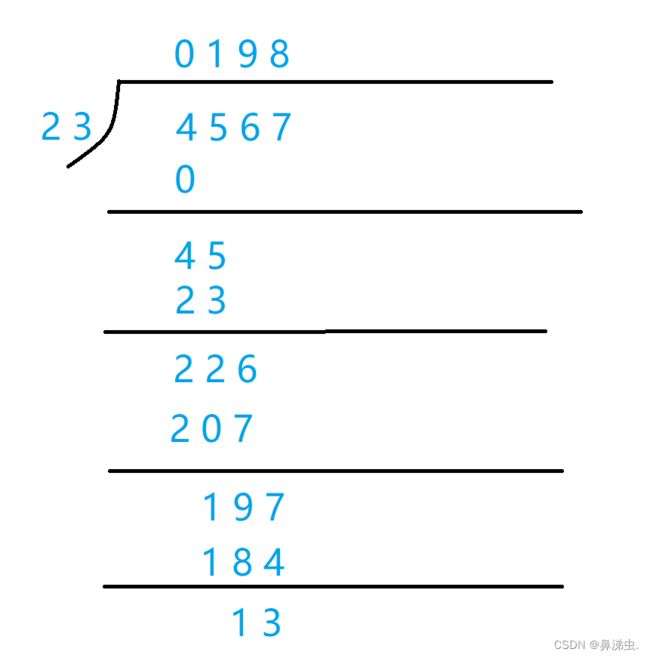
从小学的竖式计算入手:
同样,我们将这个应用于高精度计算。
高精度加法步骤
高精度数字利用字符串读入;
把字符串翻转存入两个整型数组a和b;
从低位到高位,累加,进位,存余;
把数组c从高位到低位依次输出。
算法核心
c[i] += a[i] + b[i] ;
+=: 可能前面有进位的数。
(如上述竖式计算中3+8=11保留一进一,在进行更高位2+1的计算中要加上进的这一位1)
c[i+1]= c[i] / 10 ;
在进行高位计算之前先把低位计算向高位进的数值附上。
(如竖式计算中进行2+1计算之前先把这一位数的计算结果赋初值1)
c[i] %= 10 ;
数组中的每个数只能保留一位数。
(如竖式计算3+8时在进行以上两个运算过后数值为11,但我们只要保留个位数1,因此在做最后一步计算时要去掉十位)
代码实现
#include
#include
int main() {
char s1[501], s2[501];//不超过500位数就定义长度为501的数组(最后一个存放\0)
int a[500] = { 0 }, b[500] = { 0 }, c[505] = { 0 };
//全部初始化为0
//a,b初始化为0的原因是它们位数上可能并不相同
//c初始化为0是由于核心算法中第一个算式是+=
//比如a是123,b是1234
//此时要进行运算必须在a的前面补上一个0变成0123
scanf("%s", s1);
scanf("%s", s2);
int len_a = strlen(s1);
int len_b = strlen(s2);
for (int i = len_a - 1; i >= 0; i--) {
a[i] = s1[len_a-i-1] - '0';
}//倒着赋值(注意上面图解中数组下标从低位到高位递增)
//原因:运算从低位到高位计算
//当然也可以正着赋值,只不过下面运算循环的时候要倒着循环
///核心算法也要稍微改变
for (int i = len_b - 1; i >= 0; i--) {
b[i] = s2[len_b-i-1] - '0';
}
int max = (len_a >= len_b) ? len_a : len_b;
//找到a,b的最大位数,c的位数就是max+1
for (int i = 0; i < max; i++) {
//循环条件= 0; i--) {
if (i == max && c[i] == 0)continue;
printf("%d", c[i]);
}//倒着输出
return 0;
} 高精度减法
输入两个整数 a,b(第二个可能比第一个大),计算并输出它们的差。(0≤a,b≤10^10086)。
测评网址:https://www.luogu.com.cn/problem/P2142
仍然从小学的竖式计算入手:
从低位到高位计算,不够向前借一。
当B比A大时,我们只需要将AB交换后进行计算,结果添个负号就行。
高精度减法步骤
高精度数字利用字符串读入
b. 把字符串翻转存入两个整型数组 a,b.
c. 若a
(下面代码为了输出放在一起所以没有直接判断后跟printf)
d. 从低位到高位,逐位求差,借位,存差
e. 把数组c从高位到低位依次输出;
算法核心
if (a[i] < b[i]) {
a [i+1] -- ;
a [i] = a [i] + 10 ;
}
c [i] = a [i] - b [i] ;
(不够向高位借一)
代码实现
#include
#include
#include
bool check(int len_a, int len_b, char *s1, char *s2) {
if (len_b > len_a) {
return true;
}//b位数比a大
else if (len_a == len_b) {
for (int i = 0; i < len_a; i++) {
if (s1[i] != s2[i])return s2[i] > s1[i];
}
}//位数一样b比a大
return false;//都不满足则a比b大
}
int main() {
char s1[10087], s2[10087];
int a[10086] = { 0 }, b[10086] = { 0 }, c[10086];
int flag = 1;
//flag的值作为一个是否输出负号的标志
scanf("%s", s1);
scanf("%s", s2);
int len_a = strlen(s1);
int len_b = strlen(s2);
//~i相当于i>=0,我最近在改一点点小习惯~
if (check(len_a,len_b,s1,s2)) {
//b比a大,则s1赋给b,s2赋给a
for (int i = len_a - 1; ~i; i--)b[i] = s1[len_a - i - 1] - '0';
for (int i = len_b - 1; ~i; i--)a[i] = s2[len_b - i - 1] - '0';
int t = len_a; len_a = len_b; len_b = t;
//交换的原因是因为len_c的赋值直接用len_a了
flag = 0;//改个值,方便输出时增添负号
}
else {
//a比b大,s1赋给a,s2赋给b
for (int i = len_a - 1; ~i; i--)a[i] = s1[len_a - i - 1] - '0';
for (int i = len_b - 1; ~i; i--)b[i] = s2[len_b - i - 1] - '0';
}
int len_c = len_a;//c长度取a,b中长的那个(即a)
for (int i = 0; i < len_c; i++) {
if (a[i] < b[i]) {
a[i + 1]--;
a[i] += 10;
}
c[i] = a[i] - b[i];
}
if (flag == 0)printf("-");//a比b小输出负号
for (int i = len_c - 1; c[i] == 0 && i > 0; i--)len_c--;
//把c前导零全部!去掉(区别于加法只要判断第一个)
for (int i = len_c - 1; ~i; i--) {
printf("%d", c[i]);
}
return 0;
} 高精度乘法
输入两个非负整数 a,b,计算并输出它们的积。(0≤a,b≤10^2000)。
测评网址:https://www.luogu.com.cn/problem/P1303
通过观察得规律:aibj落下来对应的c的下标为i+j,且有c的长度为a和b的长度之和!
找到了对应关系,我们再去考虑进位等一系列的问题。
高精度乘法步骤
高精度数字利用字符串读入
b. 把字符串翻转存入两个整型数组 a,b
c. 从低位到高位,累加乘积,进位,存余
d. 把数组 c从高位到低位依次输出。
算法核心
c [i+j] += a [i] * b [j] ;
+=:在低位进的数值基础上再加计算所得值
c [i+j+1] += c [i+j] / 10 ;
区别于加法为赋初值“=”(其实也可以是“+=”)
+=:循环逐渐累加(表现在竖式计算中中间区段的存在,i+j有好几种组合,如1=1+0/1+1)
c [i+j] %= 10 ;
计算结束后,只保留个位上数字
代码实现
#include
#include
int main() {
char s1[2001], s2[2001];
int a[2000], b[2000], c[4000] = { 0 };
//a,b不赋初值——区别于加法和减法
// 原因:加法减法参与运算的有前面补的0
// 但乘法参与运算的时候数组多长就只有多少的数值参与计算(不需要补0)
//c赋初值0——核心算法中的“+=”
scanf("%s", s1);
scanf("%s", s2);
int len_a = strlen(s1);
int len_b = strlen(s2);
for (int i = len_a - 1; ~i; i--)a[i] = s1[len_a - i - 1] - '0';
for (int i = len_b - 1; ~i; i--)b[i] = s2[len_b - i - 1] - '0';
int len_c = len_a + len_b;
for (int i = 0; i < len_a; i++) {
for (int j = 0; j < len_b; j++) {
c[i + j] += a[i] * b[j];
c[i + j + 1] += c[i + j] / 10;
c[i + j] %= 10;
}
}
while (c[len_c - 1] == 0 && len_c > 1)len_c--;
//用循环去掉所有前导零(当a,b中有一个为0时,前导零可能有多个)
//同时要保证结果为0时能输出一个0(别全部弄没了)
for (int i = len_c - 1; ~i; i--)printf("%d", c[i]);
return 0;
} 高精度除法
高精度除以低精度(大数字除以小数字)
输入两个整数 a,b,计算并输出它们的商(向下取整)。(0≤a≤10^5000,1≤b≤10^9)。
测评网址:https://www.luogu.com.cn/problem/P1480
根据文章上方介绍,int型可以满足10^9的数量级,因此b不是高精度数。
接下来我们来看如下除法运算:
像上述这种每一轮运算从高位到低位每次取一位数出来与前面的余数构成新数与除数进行除余的方法叫做“逐位试商法”。
我们将该方法运用于高精度除以低精度的运算中。
高精度除以低精度步骤
高精度数字利用字符串读入
把字符串顺序存入长整型数字a
从高位到低位,当前被除数,存商,求余
把数组ans从高位到低位依次输出
算法核心
ans [len_a - i - 1] = a[i] / b ;
每轮循环从高位到低位的答案存储
a [i + 1] += a[i] % b * 10 ;
后一轮循环作为被除数的数值
代码实现
#include
#include
int main() {
char s[5001];
long long a[5001], ans[5000];
//这里一定开long long!否则最后一个数据会WA
//我思来想去原因是最后一个数据中b达到了10^9的数量级
//算法核心中有a[i]+=a[i]%b*10;
//最初的时候确实是数组一块存一位数,但是在计算中累加动用到的数字要足够让b去除
//很可能达到了10^10的数量级,所以要开long long
//还有就是a至少要开5001(用到了a[i+1])
int b;
scanf("%s", s);
scanf("%d", &b);
int len_a = strlen(s);
for (int i = 0; i < len_a; i++)a[i] = s[i] - '0';
for (int i = 0; i < len_a; i++) {
ans[len_a - i - 1] = a[i] / b;
//这里为了前导零删除方便(和前面一样不用做改变)
//选择将答案倒着存储
a[i + 1] += a[i] % b * 10;
}
while (ans[len_a - 1] == 0 && len_a > 1)len_a--;//去除前导零和乘法一样
for (int i = len_a - 1; ~i; i--)printf("%d", ans[i]);
return 0;
} 我为了追求简单就这么写了,实际上这样并不太好,改变了很多东西,比如最后的a数组内部数字已经面目全非,其实完全可以像下面这样:
c[i]=(d*10+a[i])/b;
d=(d*10+a[i])%b;len_a也直接当作ans的长度用了(主要是后面len_a就用不到了懒得多定义),这个有个不好的地方就是你要是后续还想对a进行什么别的操作就很不方便了,当然对于这个短小的代码就无伤大雅了,甚至还十分短小精悍方便很很。
还有就是这个余数我没有标明,想要余数的话,把a全部赋初值0,然后最后循环结束以后的a[i+i]/10就是啦~
高精度除以高精度(大数字除以大数字)
输入两个整数 a,b,计算并输出它们的商(向下取整)。(0≤a,b≤6250!)。
测评网址:https://www.luogu.com.cn/problem/P2005
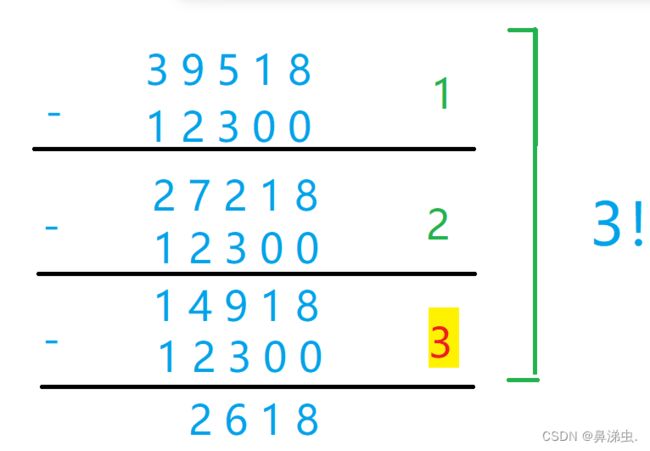
对于高精度除以高精度,直接上数据!
我们假装531518和123都是高精度数。
进行运算时,我们把除数补零(后面补零!)使之与被除数位数相同,然后被除数疯狂循环减去除数直到减不动了(再减就负数了),这时候发现一共减了四轮!重点标出的那个数字和答案的最高位一模一样!直接上手储存答案一波。(各位还能观察到补的零的个数为3,答案4的位数排在从低位到高位的第3+1位)
余数当作新的被除数,再循环进行上面的操作。
上述这种方法称作“减法模拟除法”。
高精度除以高精度步骤
高精度数字利用字符串读入
把字符串倒序存入长整型数字a
以ans的位数变化进行大循环
用temp记录每轮大循环下的被减数
大循环每次进行一位ans的计算时不断判断减数与被减数的大小关系并决定是否进行高精度减法(其中减法从高位到低位进行运算)
把数组ans从高位到低位依次输出
算法核心
不停地调整减数和被减数的位数并循环高精度减法。
代码实现
#include
#include
#include
void input(int* a) {
//输入高精度数存入a,b中
char s[10000];
int i;
scanf("%s", s);
a[0] = strlen(s);
//首个数组元素用以存放数组长度
//(好处:在传参的时候可以一并将长度传过去,不用多设参数)
for (int i = a[0]; i > 0; i--)a[i] = s[a[0] - i] - '0';
//倒着存入原因:用到高精度减法
}
void numcpy(int* p, int* q, int n) {
p[0] = q[0] + n;
//确定temp的位数
for (int i = p[0]; i >= p[0] - q[0] + 1; i--)p[i] = q[i - n];
//将b右移n位数
}
bool check(int* a, int* temp) {
//判断a和temp的大小,a>=temp返回true,反之返回false。
if (a[0] > temp[0])return true;
else if (a[0] < temp[0])return false;
//先通过位数进行比较,减少循环次数
for (int i = a[0]; i > 0; i--) {
//由高位到低位进行检查,在不等的情况下就可以直接判断
if (temp[i] > a[i])return false;
else if (a[i] > temp[i])return true;
}
return true;//一样时return true
}
void subtraction(int* a, int* temp) {
for (int i = 1; i<=a[0]; i++) {
//高精度减法
if (a[i] < temp[i]) {
a[i + 1]--;
a[i] += 10;
}
a[i] = a[i] - temp[i];
}
int i = a[0];
while (a[i] == 0) {
a[0]--;
i--;
}//不断调整a的位数,位数减去前导零的个数
}
int main() {
int a[10000], b[10000], ans[10000] = { 0 };
//这里定义的时候在洛谷里面要多加一个0才可以ac,否则会出现re数组不够大的情况
//但是因为在vs里运行的时候100000太大了会导致无法输入,所以自行在提交代码的时候加0即可。
input(a);
input(b);
ans[0] = a[0] - b[0] + 1;
//最终商的位数是被除数和除数商+1
if (ans[0] < 0) {
printf("0\n");
return 0;
}
//如果除数位数大于被除数的位数(此时除数大于被除数商为0)
for (int i = ans[0]; i > 0; i--) {
int temp[10000] = { 0 };
//定义temp来存放b经移动后的数组状态用于减法
//这里temp要时刻初始化,否则上一轮temp的高位数会为上一轮赋值的结果
numcpy(temp, b, i - 1);
//ans的位数加一,temp的位数减一
//这里i-1不是i:移动位数比ans位数少1
while (check(a, temp)) {
//如果a>temp,进行一轮减法
subtraction(a, temp);
ans[i]++;
//每进行一轮减法,ans相应位数加一
}
}
for (int i = ans[0]; i > 0; i--) {
if (i == ans[0] && ans[ans[0]] == 0)continue;
//若第一位为0,删去前导零不输出
printf("%d", ans[i]);
}
printf("\n");
return 0;
} 高精度幂次
高精度幂次步骤
高精度数字利用字符串读入
找到输入数据的小数点位置,并计算答案中小数点的位置
把字符串去除小数点转化为整数倒序存入长整型数字r
以幂次n变化进行高精度乘法大循环
用t1记录最初的r用在每轮乘法中,用t2记录每轮大循环下的积的结果并用以更新r
根据格式要求输出即可
算法核心
不停地调整乘数并循环高精度乘法。
代码实现
#include
#include
int power(int* r, int n, int len_r) {
int t1[1300] = { 0 };
int len_t1 = len_r;
for (int i = 0; i < len_r; i++)t1[i] = r[i];
//t1复制r用来做高精度乘法不变的一个乘数
//t2用来存放乘法中的临时数据
for (int i = 1; i < n; i++) {
//注意这里从1开始,且i也不能<=n而是= 0; i--) {
if (i == point && s[i] == '.')continue;
r[len_r] = s[i] - '0';
len_r++;
}//将输入的小数s去掉小数点后倒排存入数组r
len_r = power(r, n, len_r);
while (r[len_r - 1] == 0)len_r--;
//删除前导零
int zero = 0;
//zero为尾0个数
while (r[zero] == 0)zero++;
int i;
for (i = len_r - 1; i >= Ans_FracPart; i--)printf("%d", r[i]);
//输出整数部分
if ((i == Ans_FracPart - 1 && Ans_FracPart - 1 >= zero) || i == len_r - 1)printf(".");
//输出小数点(避免无小数部分时输出.以及无整数部分时要输出.)
for (int i = Ans_FracPart - 1; i >= zero; i--)printf("%d", r[i]);
//输出小数部分
printf("\n");
}
return 0;
} 终于告一段落了,看到这里都辛苦了~
有错误欢迎指出~