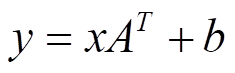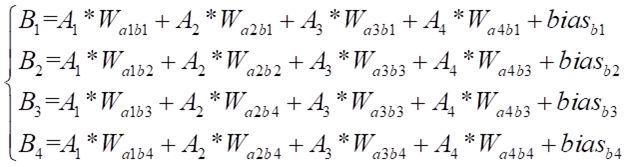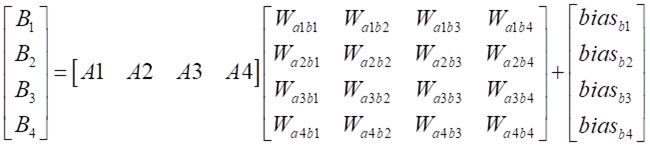Pytorch框架应用系列 之 BPNet 5-2：全连接层到矩阵计算！FC近在眼前！

专题介绍及文章命名

2020年第一更！！祝愿大家新年快乐！撸起袖子加油干！越是艰险越向前！！

专题介绍在此！希望各位读者对这个专题的各篇博客定位有全局性质的把握~~

再次提醒：该系列专题不涉及网络细节讲解，仅限于 工程实现 与 框架学习。想更多了解该专题内容请点击上文专题介绍链接。

该专题中，文章命名方式为：

Pytorch框架应用系列 之 《项目名称》 《总章节-当前章节》：《当前章节项目名称》

BP网络专题综述在此！想了解BP网络章节的文章构成？点击此处！

目录

一. 任务模型展示

二. 函数讲解
 2.1 全连接层扛把子：torch.nn.Linear
  2.1.1 函数的定义及参数功能
  2.1.2 函数的数学表达与数据格式 《子任务章节》
  2.1.3 函数的调用实例
 2.2 激活函数：torch.nn.Sigmoid
  2.2.1 函数的定义及参数功能
  2.2.2 函数的调用实例
 2.3 网络结构容器：torch.nn.Sequential
  2.3.1 函数的定义及参数功能
  2.3.2 函数的调用实例

三. 专题及章节位置信息查询

一. 任务模型展示

二. 函数讲解

2.1 全连接层扛把子：torch.nn.Linear;

注：明星函数

2.1.1 函数的定义及参数功能

首先我们先来看看官方的完整定义：

该类定义中各个参数的定义如下：

1. in_features ：全连接神经网络输入层的神经元个数;
2. out_features：全连接神经网络的输出层神经元个数；
3. bias = True：输出层神经元默认自带偏置项；

总结来讲 ：该函数可以帮我们定义两层相邻的全连接神经网络。参与计算的数据类型为Tensor。

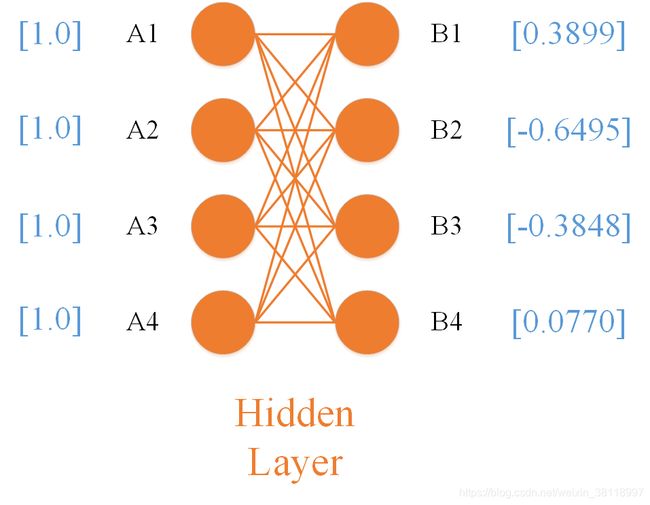
我们以模型函数中的两层全连接神经元为例，给出定义方式：

Hidden_Layer = torch.nn.Linear(4,4,True)

上述定义参数中，第一个 4 表示A1~A4共有4个输入神经元，第二个4 表示B1~B4共有4个输出神经元，True表示神经元B1~B4默认带有偏置项。

2.1.2 函数的数学表达与数据格式 《子任务章节》

本章节的子任务为： 神经网络的全连接与矩阵乘法的关系;

torch.nn.Linear 函数本质是一个矩阵计算函数，即运算参数为矩阵形式。在官方给出的 数学解释 中，其表达式如下：

上述公式中虽然仅仅 $A^T$ 我们能看出是矩阵表达，但实际上公式中的 $y$，$x$ 和 $b$ 均以矩阵形式存在，下面我们详细说说 上述网络结构是如何转换成矩阵计算并通过 torch.nn.Linear 函数计算的。首先，我们将上述网络结构中B1~B4的各层计算结果表达出来，结果如下：

虽然公式看着吓人，不过原理很简单： 就是输入层的数据乘以链接神经元的权重并求和，最后加上偏置项。学过 线性代数 的同学都知道这个东西本质就是线性方程组，写成矩阵形式如下：

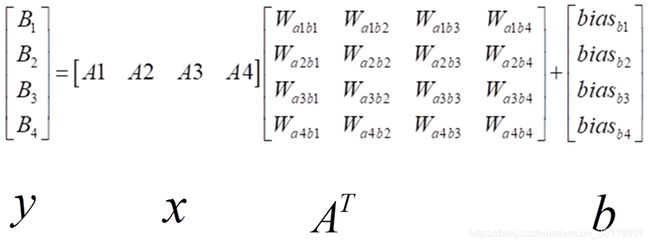
写成这种格式我们再对应一下官方给出的公式，是不是非常相似？ 基本关系我们对应一下就是：

所以 torch.nn.Linear 函数就是 通过这种方式将 全连接层表达出来的。现在我们从这个耳目一新的角度重新理解一下函数的各项输入参数：

1. in_features ：全连接神经网络输入层的神经元个数;（本质等于 $x$ 的列数）
2. out_features：全连接神经网络的输出层神经元个数；（本质等于 $y$ 的行数）
3. bias = True：输出层神经元默认自带偏置项；（由于 $b$ 的列数始终为1，行数始终与 $y$ 相等，所以不需要指定尺寸。）

现在我们提到了 $y$，$x$ 和 $b$，那为什参数里没有 $A^T$ 呢？实际上，$A^T$ 这个矩阵是 torch.nn.Linear 函数自己根据 $y$，$x$ 两者的尺寸自动计算生成的，不需要我们自己定义。 因为 $A^T$ 矩阵的本质是神经网络的权重（不信的话数一数数量是不是和给出结构图中橙色的连线数量相同），也就是需要训练的参数，所以函数会随机的初始化矩阵的值。

2.1.3 函数的调用实例

例1：单维度输入

根据 2.1.1 章节的网络结构，我们来实现一个基本的函数功能： 当A1~A4全部为 1 的时候，计算第二层B1~B4的输出值。代码如下：

import torch

#创建4X4的隐含层;
Hidden_Layler = torch.nn.Linear(4,4,True)
#创建一个数值全为 1 的 1*4 尺寸的Tensor矩阵，矩阵尺寸与2.1.2章节中的[A1 A2 A3 A4]输入尺寸保持一致;
indata = torch.ones(1,4)
#调用网络层;
output = Hidden_Layler(indata)

#打印输入数据;
print(indata)
#打印当前输出;
print(output)

输出结果打印为：

#函数输入数据;
tensor([[1., 1., 1., 1.]])
#函数输出结果;
tensor([[ 0.3899, -0.6495, -0.3848,  0.0770]], grad_fn=<AddmmBackward>)

运算功能详解：

由于 $A^T$ 权重参数矩阵 为每次调用 随机生成，所以大家在重复执行上述代码的时候没有获得相同的输出结果是完全正常的，我们需要关注的是数据格式是否与想要的结果相匹配。

例2：多维度输入

如果我们将输入矩阵由例1中的 单维度1X4 变为 多维度4X4，在原理上是满足矩阵计算条件的，那么在实际计算中的意义是什么呢？先给出大家代码：

import torch

#创建4X4的隐含层;
Hidden_Layler = torch.nn.Linear(4,4,True)
#创建一个数值全为 1 的 4*4 尺寸的Tensor矩阵;
indata = torch.ones(4,4)
#调用网络层;
output = Hidden_Layler(indata)

#打印输入数据;
print(indata)
#打印当前输出;
print(output)

输出结果打印为：

#函数输入数据;
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])
#函数输出结果;
tensor([[ 0.4007,  0.3668, -0.7145,  0.2258],
        [ 0.4007,  0.3668, -0.7145,  0.2258],
        [ 0.4007,  0.3668, -0.7145,  0.2258],
        [ 0.4007,  0.3668, -0.7145,  0.2258]], grad_fn=<AddmmBackward>)

运算功能详解：

在多维度输入的情况下我们可以理解为多个单层输入方式的叠加执行，上图中相同颜色的数据表示对应的输入内容和输出结果。在同时输入多个维度信息的条件下，我们引入batch这个概念作为理解突破点。在批处理的过程中，batch_size即为当前数据的输入维度，在模型固定的情况下，输入数据的个数是唯一确定的（即输入矩阵的列数），而行数可以由设计者自行决定，决定的方式即为 batch_size。

2.2 激活函数：torch.nn.Sigmoid;

2.2.1 函数的定义及参数功能

首先我们先来看看官方的完整定义：

总结来讲 ：该类方法会对输入的参数执行 $Sigmoid(x)=\frac{1}{1+e^{-x}}$ 的计算。参与计算的数据类型为 Tensor。

在官方文档中没有给出该类方法的传入参数，说明该类不需要进行参数定义。只需要例化后给定输入参数即可。例化方式如下：

Sigmoid = torch.nn.Sigmoid()

2.2.2 函数的调用实例

调用过程使用多维度情况向大家进行展示，单维度与多维度的差异仅仅在于输出矩阵的维度不同。实现的基本函数功能为： 将维度为4X4且数值全部为1的矩阵经过 $Sigmoid(x)$ 函数进行计算。

import torch

#创建一个全部为 1 的 4x4 Tensor矩阵;
indata = torch.ones(4,4)
#例化一个Sigmoid类型;
Sig = torch.nn.Sigmoid()
#输出Sigmoid计算结果;
Sigout = Sig(indata)

#打印当前输入;
print(indata)
#打印当前输出;
print(Sigout)

输出结果打印为：

#函数输入数据;
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])
#函数输出结果;
tensor([[0.7311, 0.7311, 0.7311, 0.7311],
        [0.7311, 0.7311, 0.7311, 0.7311],
        [0.7311, 0.7311, 0.7311, 0.7311],
        [0.7311, 0.7311, 0.7311, 0.7311]])

2.3 网络结构容器：torch.nn.Sequential;

2.3.1 函数的定义及参数功能

首先我们先来看看官方的完整定义：

总结来讲 ：该类方法可以让我们自定义网络的层叠结构并且指定网络的计算顺序。

torch.nn.Sequential 的传入参数比较特殊，我们可以理解为是模型某一层的具体结构，例如上述2.1章节中的 torch.nn.Linear 即可作为参数传入，更重要的是该功能并不限制传入参数的个数。我们以模型函数中的两层全连接神经元附带激活函数 $Sigmoid(x)$ 为例，针对下图的结构表达，给出定义方式：

model = torch.nn.Sequential(
          torch.nn.Linear(4,4,True),
          torch.nn.Sigmoid(),
        )

在对 torch.nn.Sequential 进行内部参数定义时，不需要再次对内部调用的类进行例化操作，函数会自动帮助我们承接内部的数据流向。torch.nn.Sequential 定义的结构块运算顺序根据写入类定义的顺序进行计算，自顶向下依次执行。

2.3.2 函数的调用实例

调用过程使用多维度情况向大家进行展示，单维度与多维度的差异仅仅在于输入输出矩阵的维度不同。实现的基本功能为： 当A1~A4全部为 1 的时候，计算B1~B4经过 $Sigmoid(x)$ 的输出值。

import torch

#创建一个全部为 1 的 4x4 Tensor矩阵;
indata = torch.ones(4,4)
#例化图中所示的结构块;
model = torch.nn.Sequential(
          torch.nn.Linear(4,4,True),
          torch.nn.Sigmoid(),
        )
#输出计算结果;
output = model(indata)

#打印当前输入数据;
print(indata)
#打印当前输出数据
print(output)

输出结果打印为：

#打印当前的输入数据;
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])
#打印模型的输出数据;
tensor([[0.5928, 0.7035, 0.4070, 0.5446],
        [0.5928, 0.7035, 0.4070, 0.5446],
        [0.5928, 0.7035, 0.4070, 0.5446],
        [0.5928, 0.7035, 0.4070, 0.5446]], grad_fn=<SigmoidBackward>)

三、写在最后

目前章节位置信息：

BPNet 5-1：从零开始！你的第一个神经网络！（综述）
BPNet 5-2：全连接层到矩阵计算！FC近在眼前！
BPNet 5-3：训练准备！数据集建立与载入！
BPNet 5-4：反向传播？训练函数与优化器！（待更新）
BPNet 5-5：终于等到你！BP网络的系统工程！（待更新）

(来自一名励志用“普通话”讲技术的菜狗子~)