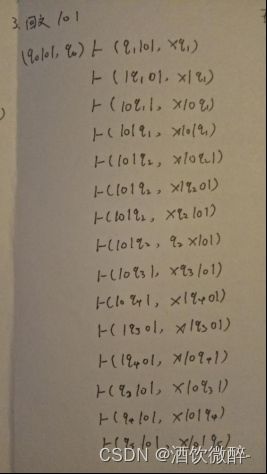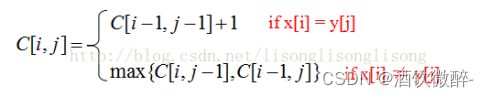算法分析与设计(耿国华第二版)
构造结果
目录
构造结果
1、矩阵连乘问题-矩阵连乘步骤P61
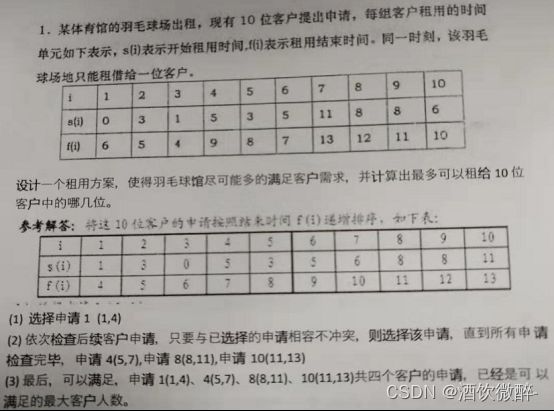
2、网球循环赛和羽毛球场地出租
3、实现回⽂识别的图灵机指令表,给出识别1001/010/0110/101序列。
4、考虑n=3的批处理作业调度实例
5、着色问题
6、0-1背包问题+背包(可分割)
7、合唱团队形问题【动态规划】(书本P57)
8、旅行商-周游路线问题
9、最长公共子序列问题
10、归并排序(mergesort)的时间复杂度
11、写出用分治算法MaxMin对下列实例寻找最大数和最小数的过程,数组A[]={48,12,61,3,5,19,32,7}
12、八数码问题求解(书本P148)
1、矩阵连乘问题-矩阵连乘步骤P61
【问题一】
设有四个矩阵A1、A2、A3、A4,它们的维数分别是:50x10,10x40,40x30,30x5考察这4个矩阵的连乘积A1×A2×A3×A4,问如确定计算阵连乘积的计算次序使得依此次序计算矩阵连乘积需要的数乘次数最少?
所以最小数乘次数为10500.最优计算次序为 A1(A2(A3 A4))。
【问题二】
【问题三】计算矩阵乘连乘M₁M₂M₃M₄,其中,M₁是30*40维,M₂是40*10维,M₃是10*8维,M₄是8*40维。用动态规划算法给出最优解表示。
解:动态规划解矩阵连乘
M1(30x40) M2(40x10) M3(10x8) M4(8x40)
设m[i][j]是计算MixMi+1x...xMj的最小值,则有:
m[1][1]=m[2][2]=m[3][3]=m[4][4]=0
m[1][2]=30x40x10=12000
m[2][3]=40x10x8=3200
m[3][4]=10x8x40=3200
m[1][3]={ m[1][2]+30x10x8=12000+2400=14400
m[2][3]+30x40x8=12800
m[2][4]={ m[2][3]+40xx8x10=3200+12800=16000
m[3][4]+40x10x40=3200+16000=19200
m[1][4]={ m[1][3]+30x8x40=12800+9600=22400
m[1][2]+ m[3][4]+30x10x40=12000+3200+12000=27200
m[2][4]+30x40x40=16000+48000=64000
建立矩阵连乘问题的递推的二维表如下:
m[1][1]=0 m[2][2]= 0 m[3][3]=0 m[4][4]=0
m[1][2]=12000 m[2][3]=3200 m[3][4]=3200
m[1][3]=12800 m[2][4]=16000
m[1][4]=22400
由上可知,这4个矩阵连乘所用到的最小乘积次数是22400
最优计算次序是(M1(M2M3))M4)
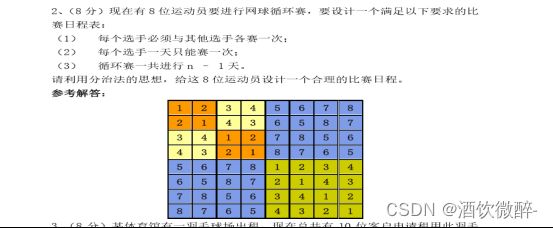
2、网球循环赛和羽毛球场地出租
网球循环赛问题描述有:
设有n=2k个运动员要进行循环赛,现设计一个满足以下要求的比赛日程表:
每个选手必须与其他n-1名选手比赛各一次:
每个选手一天至多只能赛一次;
循环赛要在最短时间内完成。
(1)如果n=2k,循环赛最少需要进行几天
(2)当n=23=8时,请画出循环赛日程表。
网球循环赛问题描述有:
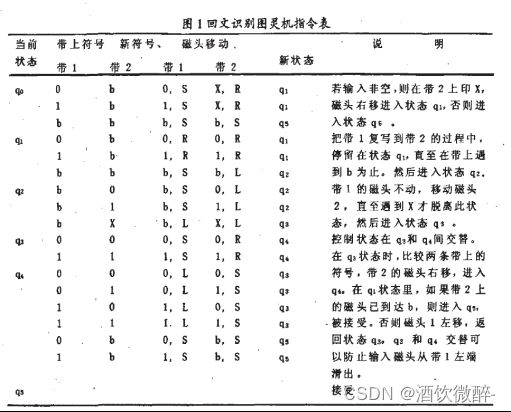
3、实现回⽂识别的图灵机指令表,给出识别1001/010/0110/101序列。
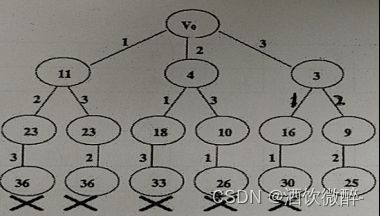
4、考虑n=3的批处理作业调度实例
(1)用优先队列式的分支限界法解该问题,画出该问题的解空间树;
(2)若当前代价f>=当前最优解代价 bestf ,则剪枝
(3)剪枝结果如图
(4)最优解为:{3,2,1},最优值为25
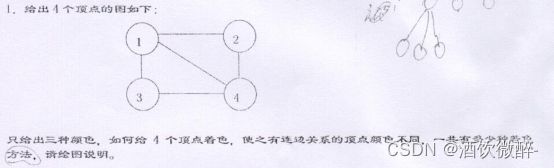
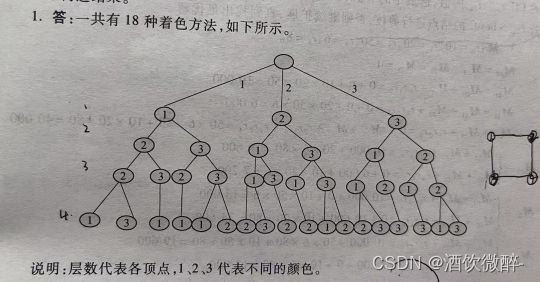
5、着色问题
【问题一】
说明:层数代表各顶点,1,2,3代表不同的颜色
【问题二】
P239类似(下面是类似题答案)
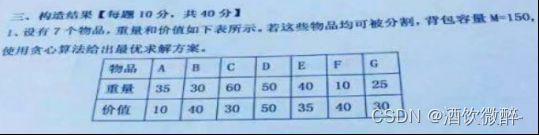
6、0-1背包问题+背包(可分割)
【可分割】
7、合唱团队形问题【动态规划】(书本P57)
【问题一】
教材p57
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 180 |
175 |
155 |
163 |
166 |
178 |
182 |
160 |
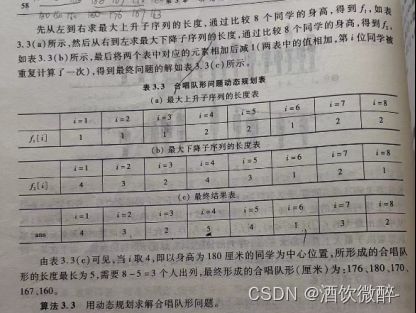
最⼤上升⼦序列的长度表
| i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| F1(i) |
1 |
1 |
1 |
2 |
3 |
4 |
5 |
2 |
最⼤下降⼦序列的长度表
| i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| F2(i) |
4 |
3 |
1 |
2 |
2 |
2 |
2 |
1 |
结果表
| i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| ans |
4 |
3 |
1 |
3 |
4 |
5 |
6 |
2 |
由结果表可以看出,应该以第 7 个同学为中⼼位置,需要 8-6=2 个学⽣出列,最终形成的
合唱队列为155,163,166,178,182,160
【问题二】
8、旅行商-周游路线问题
【问题一】
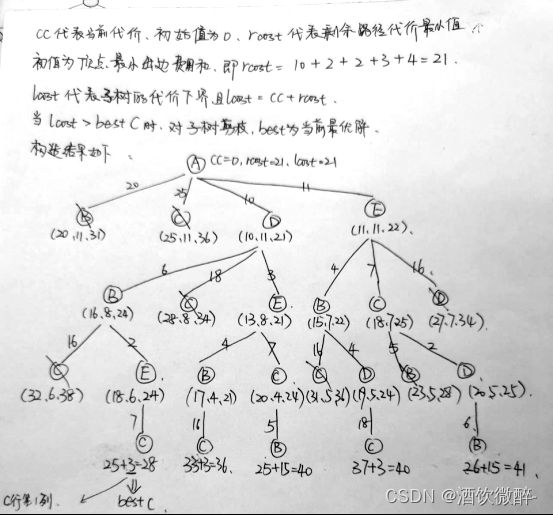
给定n=5,代价矩阵如下,用分支限界法给出其状态空间树,找出最小代价周游路线。
9、最长公共子序列问题
【问题一】
给定两个字符串X=(A,B,C,B,D,A,B)和Y=(B,D,C,A,B,A),利用动态规划方法求解这两个字符串的最长公共子序列。要求给出计算最优值的递归方程。求最长公共子序列过程。
10、归并排序(mergesort)的时间复杂度
11、写出用分治算法MaxMin对下列实例寻找最大数和最小数的过程,数组A[]={48,12,61,3,5,19,32,7}
12、八数码问题求解(书本P148)
【问题一】
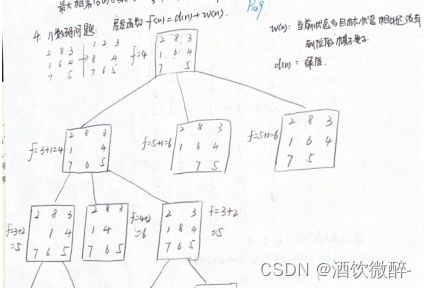
在八数码问题中,设一个启发函数f(n)=d(n)+w(n),其中d(n)为搜索树中节点的深度(根在第0层),对应已经走过的路径长度;w(n)为当前结点n的状态描述中与目标状态相比较还没有到位的棋子数,近似对应将来还要走的路径长度。现采用优先队列式分支限界法来解决8数码问题,请画出解空间树。
初始布局和目标布局如下图所示:
答:仅为空格制定这左、上、右、下种走步,空格移动的唯一约束是不能移出棋盘。