【数据结构】树的遍历
树的遍历
前序遍历
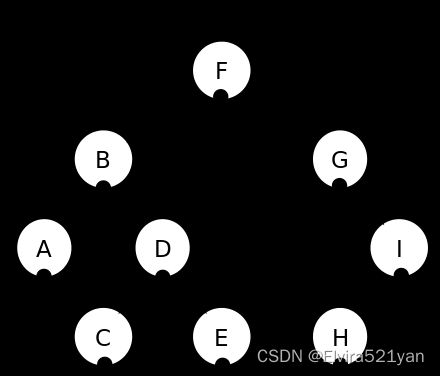
图片来源维基百科深度优先遍历(前序遍历): F, B, A, D, C, E, G, I, H.
代码实现
递归
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
# @param root TreeNode类
# @return int整型一维数组
class Solution:
def preorderTraversal(self , root: TreeNode) -> List[int]:
# write code here
if not root:
return []
return [root.val] + self.preorderTraversal(root.left) + self.preorderTraversal(root.right)
非递归
class Solution:
def preorderTraversal(self , root: TreeNode) -> List[int]:
# write code here
if not root:
return []
node_stack = []
ans = []
node_stack.append(root)
while node_stack:
node = node_stack.pop(-1)
if node.right:
node_stack.append(node.right)
if node.left:
node_stack.append(node.left)
ans.append(node.val)
return ans
牛客 BM23 二叉树的前序遍历
中序遍历
中序遍历是按照左子树->根节点->右子树的顺序进行遍历
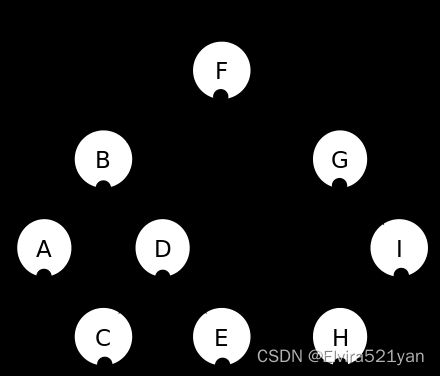
图片来源维基百科深度优先遍历(中序遍历): A, B, C, D, E, F, G, H, I.
代码实现
递归
class Solution:
def inorderTraversal(self , root: TreeNode) -> List[int]:
# write code here
if not root:
return []
return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)
非递归
class Solution:
def inorderTraversal(self , root: TreeNode) -> List[int]:
# write code here
if not root:
return []
node_stack = []
ans = []
while node_stack or root:
while root:
node_stack.append(root)
root = root.left
node = node_stack.pop(-1)
ans.append(node.val)
root = node.right
return ans
牛客 BM24 二叉树的中序遍历
后序遍历
中序遍历是按照左子树->右子树->根节点的顺序进行遍历
图片来源维基百科深度优先搜索(后序遍历):A, C, E, D, B, H, I, G, F.
代码实现
递归
class Solution:
def postorderTraversal(self , root: TreeNode) -> List[int]:
# write code here
if not root:
return []
return self.postorderTraversal(root.left) + self.postorderTraversal(root.right) + [root.val]
非递归
class Solution:
def postorderTraversal(self , root: TreeNode) -> List[int]:
# write code here
if not root:
return []
pre = None
node_stack = []
ans = []
while root or node_stack:
# 每次先找到最左边的节点
while root:
node_stack.append(root)
root = root.left
node = node_stack.pop(-1)
# 如果该元素的右边没有或是已经访问过
if not node.right or node.right is pre:
ans.append(node.val)
pre = node
else:
node_stack.append(node)
root = node.right
return ans
层次遍历
层次遍历是按照从上往下、从左往右一层层进行遍历
图片来源维基百科广度优先遍历 - 层次遍历:F, B, G, A, D, I, C, E, H.
方法
- 判断二叉树是否为空,空树返回空列表。
- 建立辅助队列,根节点入队。
- 每次进入一层,统计队列中元素的个数。因为每当访问完一层,下一层作为这一层的子节点,一定都加入队列,而再下一层还没有加入,因此此时队列中的元素个数就是这一层的元素个数。
- 每次遍历一层对应元素数量的节点,将其依次从队列中弹出,数值加入该层结果列表,若存在子节点,依次加入队列排队等待访问。
- 访问完这一层的元素后,将这个一维数组加入二维数组中,再访问下一层。
代码实现
class Solution:
def levelOrder(self , root: TreeNode) -> List[List[int]]:
# write code here
if not root:
return []
node_queue = []
ans = []
node_queue.append(root)
while node_queue:
ans_row = []
n = len(node_queue)
for i in range(n):
node = node_queue.pop(0)
ans_row.append(node.val)
if node.left:
node_queue.append(node.left)
if node.right:
node_queue.append(node.right)
ans.append(ans_row)
return ans