JS 排序算法详解（冒泡排序，选择排序，插入排序，希尔排序，快速排序）

JS 排序算法详解（冒泡排序，选择排序，插入排序，希尔排序，快速排序）

一、 大O表示法

在进行排序算法之前，我们得先掌握一种对算法效率的表示方法，大O表示法。

我们使用大O表示法来表示算法的时间复杂度，是用来表示算法的速度随着数据量的变化而如何变化的。

常见的大O表示函数：

• O(1)：常数的
• O(log n)：对数的
• O(n)：线性的
• O(n*log(n))：线性和对数乘积
• O(n²)：平方
• O(2ⁿ)：指数

推导大O表示法的方式：

• 用 常量1取代运行时间中所有的加法常量
• 在修改后的运行次数函数中，只保留最高阶项
• 如果最高存在且不为1，则去除与这个项相乘的常数

二、排序算法

排序算法有很多很多，这里就不全部实现，只实现一些比较常见的排序算法。

简单排序：冒泡排序、选择排序、插入排序
高级排序：希尔排序、快速排序

1.冒泡排序

冒泡排序算法相对其他排序运行效率较低，但是它是最简单的一种排序。

原理：冒泡排序的原理（以递增序为例）是每次从头开始依次比较相邻的两个元素，如果后面一个元素比前一个要小，说明顺序不对，则将它们交换，本次循环完毕之后再次从头开始扫描，直到某次扫描中没有元素交换，说明每个元素都不比它后面的元素大，至此排序完成。

过程：

代码：

// 冒泡排序
function bubbleSort (array) {
  for(var i = 0; i < array.length - 1; i++) {         // 表示比较的趟数
    for(var j = 0; j < array.length - i - 1; j++) {   // 表示比较的次数
      if(array[j] > array[j+1]) {  
        var temp = array[j+1];    
        array[j+1] = array[j];
        array[j] = temp;
      }
    }
  }
}
// 测试
var array = [3,24,7,1,2,10,6,12];
bubbleSort(array);
console.log(array.toString());
// 结果为：1,2,3,6,7,10,12,24

效率：

1. 冒泡排序的比较次数：
   通过大O表示法来推导过程，n个数字比较时，第一次循环比较n-1次，第二次循环比较n-2次，第三次比较n-3次，…，直到最后一次比较1次。
   比较次数：(n-1)+(n-2)+(n-3)+ … +3+2+1
   所以比较次数是：n*(n-1)/2
   根据大O表示法只保留最高阶项，去除常量，只剩n*n
2. 冒泡排序的交换次数：
   交换次数不是确定的，所以以每两次比较交换一次来进行计算
   交换次数：n*(n-1)/4
   根据大O表示法只保留最高阶项，去除常量，只剩n*n

因此冒泡排序的大O表示法为O(n²)

2.选择排序

选择排序可以看作是冒泡排序的改进版本。
思路：选择排序，从头至尾扫描序列，找出最小的一个元素，和第一个元素交换，接着从剩下的元素中继续这种选择和交换方式，最终得到一个有序序列。
过程：

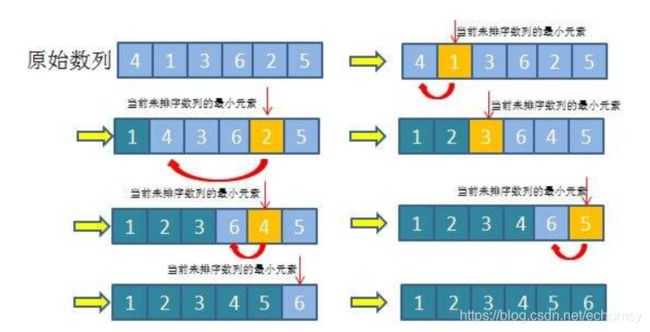
代码：

// 选择排序
function selectionSort(array) {
  var min;
  for(var i = 0; i < array.length - 1; i++) {   // 外层循环，从0位置开始取数据
    min = i;
    for(var j = i + 1; j < array.length; j++) { // 内层循环，从i+1位置开始选择出最小的数据
      if(array[min] > array[j]) {
        min = j;              // 找到小的数据，并且对min赋值
      }
    }
    var temp = array[min];    // 此时最小的数据就是第min个位置的数据,min和i位置数据交换
    array[min] = array[i];
    array[i] = temp;
  }
}
// 测试
var array = [4,8,2,7,3,1];
selectionSort(array);
console.log(array.toString());
// 结果为：1,2,3,4,7,8

效率：

1. 选择排序的比较次数：
   选择排序和冒泡排序的比较次数都是：n*(n-1)/2
   用大O表示法都是O(n²)
2. 选择排序的交换次数：
   选择排序每次进行选择时，最多需要交换1次，一共遍历n-1次
   用大O表示法就是O(n)
   所以选择排序通常认为在执行效率上是高于冒泡排序的

3.插入排序

插入排序是简单排序中效率最好的一种，而且插入排序也是学习其他高级排序的基础。
思路：
将待排序序列中第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列，从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。
过程：

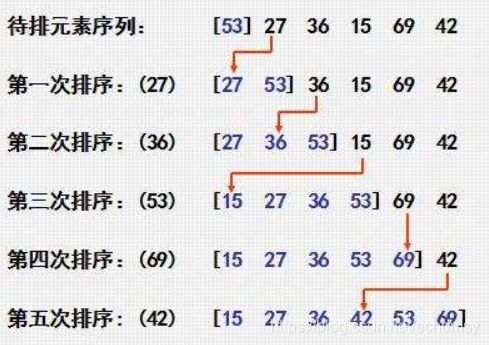
代码：

// 插入排序
function insertionSort(array) {
  for(var i = 1; i < array.length; i++) {    // 外层循环，从第1个位置开始获取数据，向前面局部有序进行插入
    var temp = array[i]; // 取出要插入的元素
    var j = i; 
    while(array[j - 1] > temp && j > 0) {    // 内层循环，将要插入的元素和前面的元素依次进行比较，找到合适的插入位置
      array[j] = array[j-1];
      j--;
    }
    // 将temp放置到j位置上
    array[j] = temp;
  }
}

效率：

1. 插入排序的比较次数：
   第一次最多需要比较1次，第二次最多需要比较2次，……，最后一次最多需要比较n-1次。
   因此插入排序的最多比较次数是1+2+3+…+n-1 = n*(n-1)/2
   但是每次插入我们大概只需要进行一半的比较
   所以插入排序的比较次数为n*(n-1)/4， 相对于冒泡和选择排序，比较次数少了一半。
2. 插入排序的复制次数：
   第一次最多需要复制1次，第二次最多需要复制2次，……，最后一次最多需要复制n-1次。
   因此插入排序的最多复制次数是n*(n-1)/2
   但是每次复制我们大概只需要进行一半的复制
   所以插入排序的复制次数为n*(n-1)/4

4.希尔排序

希尔排序是插入排序的一种高效的改进版，并且效率比插入排序更快。
插入排序的问题：
由于希尔排序基于插入排序，所以我们需要回顾一下插入排序以及它的问题。
插入排序的问题：
假设一个较小的数据项在很靠近右端的位置上，这里本来应该时较大的数据项的位置，要把这个小数据项移动到左边的正确位置，所有的中间数据项都必须向右移动一位，每个步骤对数据项都进行n次复制，平均下来就是移动n/2次，n个元素就是n*n/2= n²/2，所以插入排序的效率时O(n²)。
如果有某种方式，不需要一个个移动所有中间的数据项，就能把较小的数据项移动到左边，那么算法的执行效率就会有很大的改进。

思路：
希尔排序就是把无序的数组分割成很多的子序列，子序列不是逐段分割的，而是相隔特定增量的子序列，对各个子序列进行插入排序，然后再选择一个更小的增量，将之前排序后的数组按这个增量分割成多个子序列，对各个子序列进行插入排序，……，不断选择更小的增量，直到增量为1时，再对序列进行一次插入排序，使序列最终成为有序序列，即排序完成。

希尔排序增量的选择：
初始增量为n/2，下一次的增量为原来的1/2，直到增量为1。
比如对于n = 100的数组，增量间隔序列为：50，25，12，6，3，1
过程：

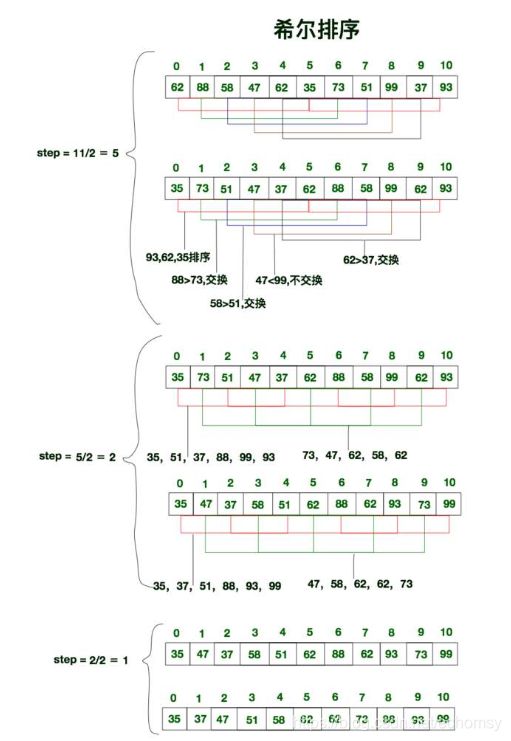
代码：

// 希尔排序
function shellSort(array) {
  // 获取数组的长度
  var length = array.length;
  // 初始化增量
  var gap = Math.floor(length / 2);
  // 循环让gap不断减小，直到为1
  while(gap >= 1) {
    // 以gap为间隔，进行分组，对分组进行插入排序
    for(var i = gap; i < length; i++) {
      var temp = array[i];
      var j = i;
      while(array[j-gap] > temp && j > gap - 1) {
        array[j] = array[j - gap]; 
        j -= gap;
      }
      // 将j位置的元素赋值temp
      array[j] = temp;
    }
    // 增量变化
    gap = Math.floor(gap / 2);
  }
}

// 测试：
var array = [62,88,58,47,61,35,73,51,99,37,93];
shellSort(array);
console.log(array.toString());
// 结果为：35,37,47,51,58,61,62,73,88,93,99

效率：
希尔排序的效率和增量是有关系的，但是，它的效率证明非常困难，甚至某些增量的效率至今没有呗证明出来。但是经过统计，希尔排序使用原始增量，最坏情况下的的时间复杂度为O(n²)，通常都要好于O(n²)。
总之，我们使用希尔排序大多数情况下效率都高于简单排序。

5.快速排序

快速排序几乎可以说是目前所有排序算法中，最快的一种排序算法。
快速排序其实是冒泡排序的升级版本，冒泡排序需要经过很多次交换，才能在一次循环中，将最大值放在正确的位置，而快速排序可以在一次循环中，找到某个元素的正确位置，并且该元素之后也不需要任何移动。
快速排序的思想就是分而治之。
思路：
快速排序采用分而治之的思想，将待排序的数中取出一个数作为基准数，将比这个数大的数字全部放在它的右边，比这个数字小的或者等于的全部放在它的左边，再对左右区间重复第二步，直到各个区间只有一个数。基准值我选择数组的第一项。
过程：

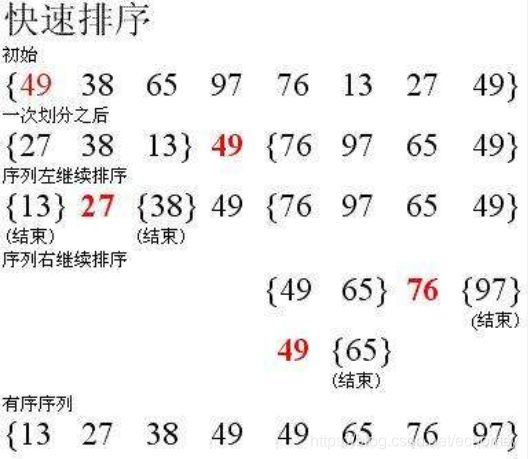
代码：

// 快排顶层调用函数
function quickSort(arr) {
  return quick(arr, 0, arr.length-1);
}
// 快排递归调用函数
function quick(arr, start, end) {
  var base = arr[start];
  var i = start, j = end;
  if(i >= j) return [];
  while(i < j) {
    while( i < j && arr[j] >= base) j--;
    arr[i] = arr[j];
    while( i <j && arr[i] < base) i++;
    arr[j] = arr[i];
  }
  arr[i] = base;
  quick(arr, start, i-1);
  quick(arr, i+1, end);
  return arr;
}

var array = [8,7,9,48,1,59,65,14,18,7,3,84,159];
var res = quickSort(array);
console.log(res);
// 结果为：[1,  3,  7,  7,  8,  9,14, 18, 48, 59, 65, 84, 159]

效率：
快速排序被认为是速度最快的排序算法。
快速排序的平均速率是O(n * log n)

（如果有什么错误，欢迎大佬在评论区指正，thank you~）