数据结构八大排序之快速排序算法

数据结构八大排序之快速排序算法

算法思想如下:
1、选择基准元素：从待排序的数组中选择一个元素作为基准（pivot）。可以选择数组的第一个元素、最后一个元素或者随机位置的元素作为基准。
2、划分操作：将数组中的其他元素按照与基准的大小关系进行划分，将比基准小的元素放在基准的左侧，比基准大的元素放在基准的右侧。同时，基准元素所在的位置也确定了。
3、递归排序：对基准元素左侧和右侧的子数组分别进行递归调用快速排序算法，重复上述步骤，直到子数组的长度为1或0（即已经有序）。
4、合并结果：递归调用的过程中，子数组的排序会不断地将基准元素放置在正确的位置上，最终整个数组就变为有序。

该算法在前端中的应用

目前我知道的：js的数组操作方法sort这个api的实现原理就是快速排序算法。

代码实现

// 快速排序算法 
function quickSort(arr:number[],type:SortType):number[] {
    // 当数组中只有一项则直接返回 且也是结束递归的出口
    if(arr.length<=1) return arr
    // 基准元素的索引
    const pivotIndex = Math.floor(arr.length/2)
    // 基准元素的值
    const pivot = arr[pivotIndex]
    // 将小于基准元素的值放入该数组中
    const less:number[] = []
    // 将等于基准元素的值放入该数组中
    const equal:number[] = []
    // 将大于基准元素的值放入该数组中
    const greater:number[] = []
    // 遍历数组进行切分 
    for(const element of arr) {
        (element < pivot)? less.push(element):undefined;
        (element > pivot)? greater.push(element):undefined;
        (element == pivot)? equal.push(element):undefined
    }
    // 升序排列 递归
    if(type==SortType.Asc) return [...quickSort(less,SortType.Asc),...equal,...quickSort(greater,SortType.Asc)]
    // 降序排列
    else return [...quickSort(greater,SortType.Desc),...equal,...quickSort(less,SortType.Desc)]
}

算法的使用

以下面这个数组为例子，算法接收两个参数，第一个参数是待排序的数组，第二个参数指定待排序的规则（升序还是降序).

const sortArr = [5,3,6,2,9,1]

实现数组升序排列：

const newArr = quickSort(sortArr,SortType.Asc)
console.log('使用快速排序实现数组的升序排列',newArr)

实现数组降序排列：

const newArr = quickSort(sortArr,SortType.Desc)
console.log('使用快速排序实现数组的降序排列',newArr)

执行过程详解

1、选择基准元素：在这个例子中，我们选择数组的第一个元素作为基准，即 5。

2、划分操作：将数组中的其他元素按照与基准的大小关系进行划分。比基准小的元素放在基准的左侧，比基准大的元素放在基准的右侧。

• 第一次划分：将数组划分为 [3, 2, 1]、[5]、[6, 9] 三部分。
• 第二次划分：对左侧的子数组 [3, 2, 1] 进行划分，得到 [2, 1]、[3]。
• 第三次划分：对右侧的子数组 [6, 9] 进行划分，得到 [6]、[9]。
  最终的划分结果为 [2, 1, 3, 5, 6, 9]。

3、递归排序：对基准元素左侧和右侧的子数组分别进行递归调用快速排序算法。
对左侧子数组 [2, 1, 3] 进行快速排序。

• 选择基准元素 2。
  划分结果为 [1]、[2]、[3]。
  对右侧子数组 [6, 9] 进行快速排序。
• 选择基准元素 6。
  划分结果为 [6]、[9]。
  4、合并结果：递归调用的过程中，子数组的排序会不断地将基准元素放置在正确的位置上，最终整个数组就变为有序。

最终排序结果为 [1, 2, 3, 5, 6, 9]。
选择基准元素，这个元素尽量能将数组划分成两个相同长度的表，长度越接近越好，因为这样可以减少递归的深度，节省性能，

假如你选择的基准元素不好，我们来调试一下，看一下效果：

上面的情况是对于数组几乎有序或者已经有序，并且每次基准元素选择数组的第一项的时候，这时候性能开销最大，其时间复杂度为O(n²)，当然如果数据量小，那确实无所谓，几乎看不出什么。
下面是选择基准元素适中的情况，我们再来看一下运行过程中的状态:

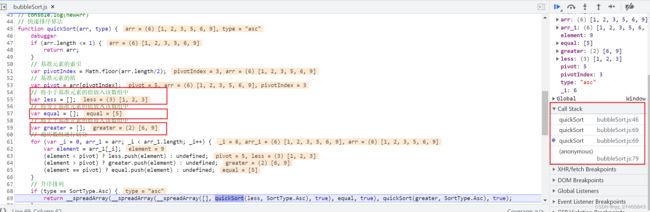
两图对比一下，第二张图，基准元素选择适中，递归深度减少一半，性能开销小，两个子表几乎相同，其时间复杂度为O(nlogn)，这就等同于一颗二叉树，左孩子与右孩子高度相同，它相比于第一张图的单只树(只有右孩子没有左孩子)，那肯定是单只树的性能开销比较大。当数据量过大的时候，受基准元素选择不好以及待排序数组的影响，爆栈都有可能。

算法总结

快速排序算法的性能在八大排序中算得上是优秀的。
其平均时间复杂度是O(nlogn) 。其中划分子表的时间复杂度是logn级别，对子表排序的时间复杂度是n级别。
空间复杂度是O(n),开辟了三个长度为n的数组，总体为O(n)级别.
文章来源：炸药包一号