【机器学习】李宏毅——Flow-based Generative Models
前文我介绍了部分关于生成学习的内容,可以参考我这篇博文点此
前面介绍的各个生成模型,都存在一定的问题:
- 对于PixelRNN这类模型来说,就是从左上角的像素开始一个个地进行生成,那么这个生成顺序是否合理,每一个像素是否只与它前面的像素有关,这就是其问题
- VAE的问题在前文就已经提到,它只能够学会模仿训练集中的例子,无法真正做到“创造”
- 对于GAN来说可能是生成方面最好的模型,但是实在是太难训练了
因此我们接下来要介绍的流形生成模型,就是用多个比较简单的生成器进行串联,来达到用简单的分布转换成复杂的分布的效果。
Generator
一般来说,生成器是一个神经网络,其定义了一个概率分布。例如我们有一个生成器G如下图,那么我们输入一个z,就可以得到输出x;而z我们可以看成是从简单的正态分布中采样得来的,而最终得到的x的分布则可以认为跟生成器G相关,因此定义该分布为 P G ( x ) P_G(x) PG(x)。这里可以将x称为观测变量,也就是我们实际能够得到的样本;将z称为隐变量,其对于样本的生成式至关重要的。因此可以认为观测变量x的真实分布为 P d a t a ( x ) P_{data}(x) Pdata(x),如下图:
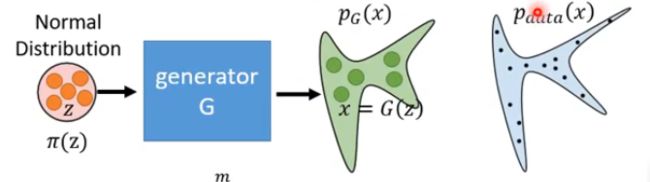
那么我们调整生成器的目的就是希望 P G ( x ) P_G(x) PG(x)和 P d a t a ( x ) P_{data}(x) Pdata(x)能够越接近越好,即:
G ∗ = a r g m a x G ∑ i = 1 m l o g P G ( x i ) ⇔ a r g m i n G K L ( P d a t a ∣ ∣ P G ) G^*=argmax_G\sum_{i=1}^mlogP_G(x^i)\Leftrightarrow argmin_GKL(P_{data}\mid \mid P_G) G∗=argmaxGi=1∑mlogPG(xi)⇔argminGKL(Pdata∣∣PG)
其中, x i x^i xi是从分布 P d a t a P_{data} Pdata中采样得到的。那么求解生成器G也就是极大似然的求解,也就是最大化每个样本被采样得到的概率,这相当于极小化那两个分布的KL散度,是满足我们的预期的。
Math Background
Jacobian Matrix
雅可比矩阵可以通过下图来简单理解:
那么存在一个重要的性质是:
J f × J f − 1 = I d e t ( J f ) = 1 d e t ( J f − 1 ) J_f\times J_{f^{-1}}=I\\ det(J_f)=\frac{1}{det(J_{f^{-1}})} Jf×Jf−1=Idet(Jf)=det(Jf−1)1
即它们互为逆矩阵,且行列式也存在互为倒数的关系。而行列式还有另外一个含义,就是将矩阵的每一行都当成一个向量,并在对应维度的空间中展开,那么形成的那个空间的“体积“就是行列式的绝对值,如下图的二维的面积和三维的体积:
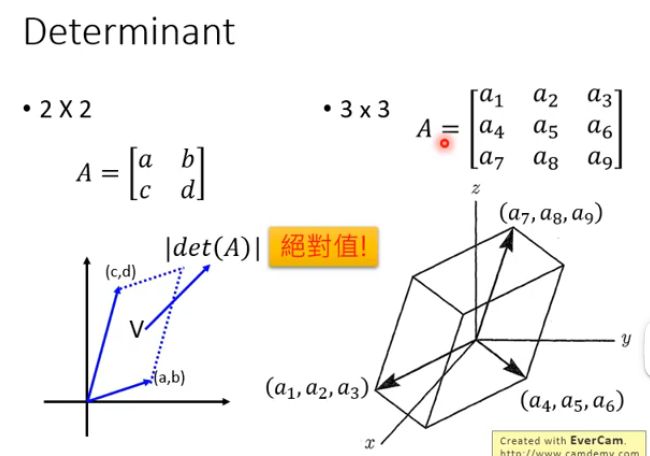
Change of Variable Theorem
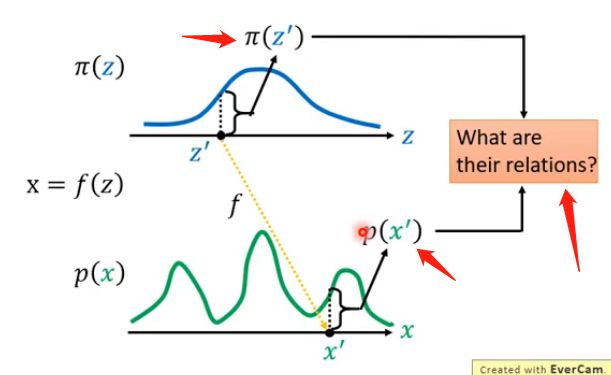
根据前面的描述,我们已知了z的分布,假设当前也知道了x的分布,那么我们想要的是求出来生成器G,或者说求出来怎么从z的分布转换到x的分布,如下图:
我们先从最简单的情形来介绍我们具体解决问题的方式。
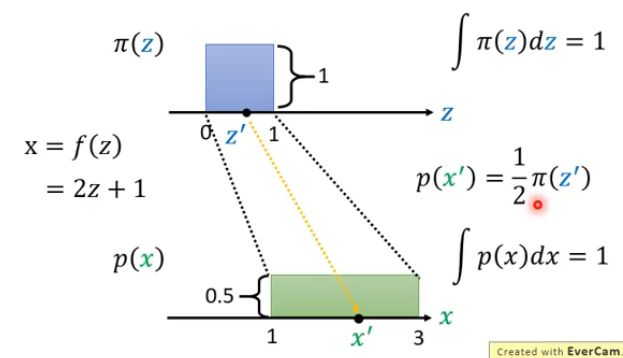
假设当前z满足的分布为一个0到1之间的均匀分布,而z和x之间的关系已知,为 x = f ( z ) = 2 z + 1 x=f(z)=2z+1 x=f(z)=2z+1,那么就可以得到下面的图形。而由于两者都是概率分布,因此两者的积分都应该为1(面积相同),因此可以解出来x的分布对应的高度为0.5。
那么假设z和x的分布都为更加复杂的情况,那我们可以在某点 z ′ z' z′上取一定的增量 Δ z \Delta z Δz,那么对应映射到x的分布上就也有 x ′ x' x′和 Δ x \Delta x Δx。那么假设 Δ z \Delta z Δz很小,可以使得在该段之内的 p ( z ) p(z) p(z)都相同, p ( x ) p(x) p(x)也同理相等,再根据这两部分的面积相同即可得到:
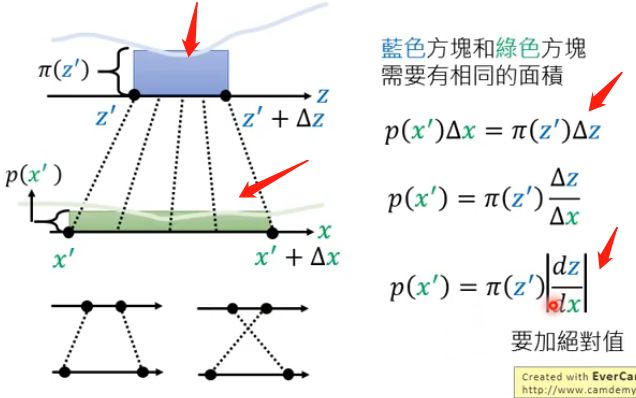
需要注意的是转换成微分之后需要加上绝对值,因为微分可正可负。
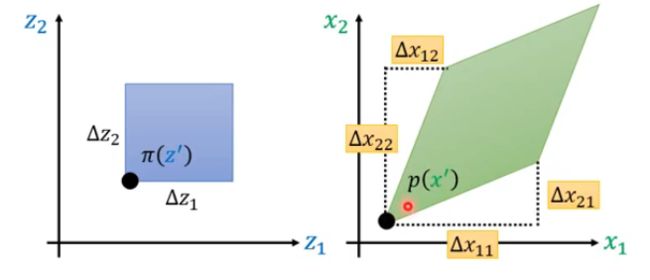
那么接下来拓展到二维空间,假设当前的 π ( z ′ ) \pi(z') π(z′)处对于两个方向都进行了增量,那么映射到x之中将会有四个增量:其中 Δ x 11 \Delta x_{11} Δx11表示 z 1 z_1 z1改变的时候 x 1 x_1 x1的改变量, Δ x 12 \Delta x_{12} Δx12表示 z 1 z_1 z1改变的时候 x 2 x_2 x2的改变量,以此类推,因此在x的空间中就扩展为一个菱形。
那么它们之间存在的关系从面积相等拓展到了体积相等,即:
p ( x ′ ) ∣ d e t [ Δ x 11 Δ x 21 Δ x 12 Δ x 22 ] ∣ = π ( z ′ ) Δ z 1 Δ z 2 p(x')\lvert det\left[ \begin{matrix} \Delta x_{11}~ \Delta x_{21} \\ \Delta x_{12}~\Delta x_{22} \end{matrix} \right] \rvert =\pi(z')\Delta z_1 \Delta z_2 p(x′)∣det[Δx11 Δx21Δx12 Δx22]∣=π(z′)Δz1Δz2
也就是两个图形的面积和在对应点的取值的乘积相等。那么对上式进行推导:
可以发现两者分布之间相差为雅克比矩阵的行列式的绝对值。
Flow-based Model
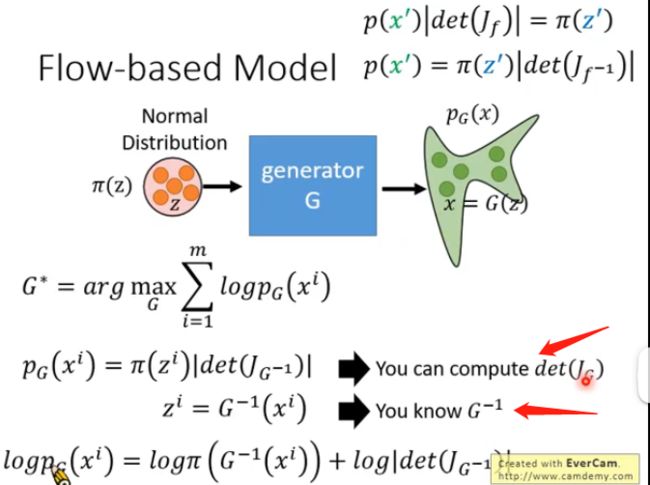
经过上面的各种推导,我们可以将目标函数进行转换:
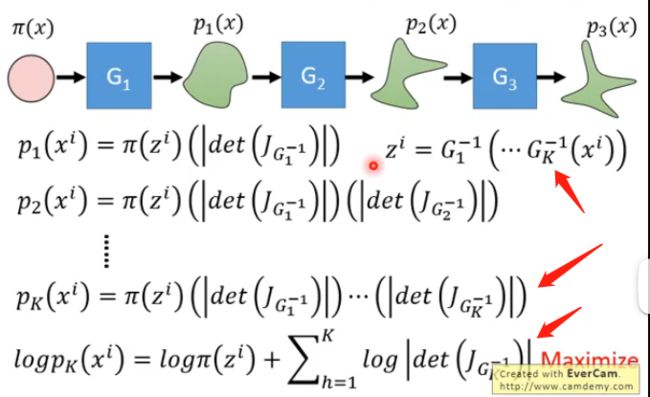
而我们如果要最大化最下面的式子,我们首先需要知道怎么算雅克比矩阵的行列式,这在当矩阵的大小很大的时候是非常耗时的;其次是要知道怎么算生成器G的逆 G − 1 G^{-1} G−1,这个会要求输入的维度和输出的维度必须是一样的,因此我们要巧妙地设计网络的架构,使其能够方便计算雅克比矩阵的行列式和生成器的逆 G − 1 G^{-1} G−1。而在实际的Flow-based Model中,G可能不止一个。因为上述的条件意味着我们需要对G加上种种限制。那么单独一个加上各种限制就比较麻烦,我们可以将限制分散于多个G,再通过多个G的串联来实现,这也是称为流形的原因之一:
因此要最大化的目标函数也变成了:
l o g p K ( x i ) = l o g π ( G − 1 ( x i ) ) + ∑ h = 1 K l o g ∣ d e t ( J G h − 1 ) ∣ logp_K(x^i)=log\pi(G^{-1}(x^i))+\sum_{h=1}^Klog\lvert det(J_{G_h^{-1}}) \rvert logpK(xi)=logπ(G−1(xi))+h=1∑Klog∣det(JGh−1)∣
可以发现上述要最大化的目标函数中只有 G − 1 G^{-1} G−1,因此在训练的时候我们可以只训练 G − 1 G^{-1} G−1,其接受x作为输入,输出为z;而在训练完成后就将其反过来,接受z作为输入,输出为x。
因为我们在训练的时候就会从分布中采样得到x,然后代入得到z,并且根据最大化上式来调整 G − 1 G^{-1} G−1。那么如果只看上式的第一项,因为 π ( t ) \pi(t) π(t)是正态分布,因此当t取零向量的时候其会达到最大值,因此如果只求第一项的最大化的话会使得我们输出的z向量都变成零向量。但是这会导致雅克比矩阵全为0(因为z都是零向量,因此没有变化的梯度),那么第二项将会冲向负无穷,因此这两项之间是相互约束的关系!第一项使得所有的z向量都往零向量附近靠近,第二项使得z向量都全部为零向量。
Coupling Layer
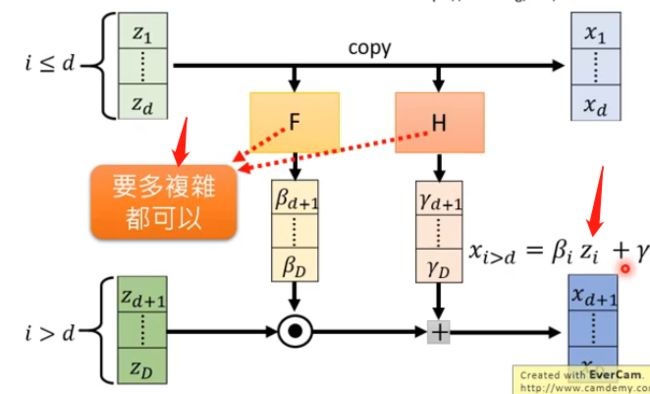
为了能够方便计算雅克比矩阵,因此我们采用Coupling Layer这种思想,即我们假设z和x之间满足这种关系:
其中F和H是两个函数,进行向量的变换而已,它有多复杂都是可以的。而上图是正向的过程,因为我们训练的时候是训练 G − 1 G^{-1} G−1,因此我们需要负向的过程,即如下:
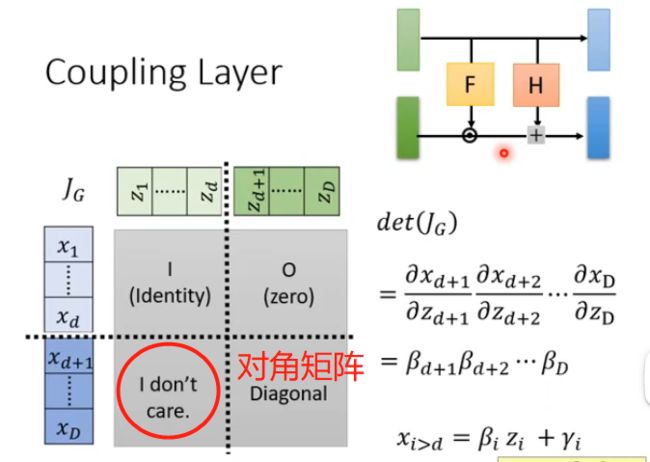
因此满足了上述关系之后,雅克比矩阵的计算就变得很方便了:
首先解释一下为什么左下角那个复杂的块矩阵我们不用注意:因为右上角是零矩阵,因此在计算行列式的时候只会关注右下角矩阵的值而不会管左下角矩阵的值是多少。
因此对于这种关系的变换我们就可以很方便的求出雅克比矩阵行列式的值。
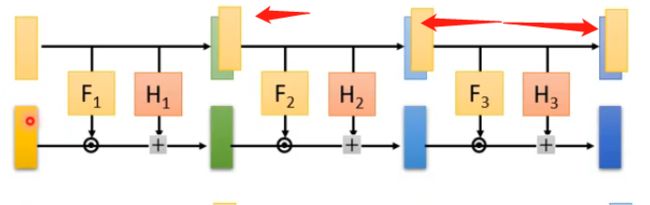
再接下来我们就可以将多个Coupling Layer串在一起,但如果正向直接串的话就会发现前d维度的值是直接拷贝的,从头到尾都相同,这并不是我们想要的结果,我们不是希望前d维度的值一直保持不变:
那么可能的解决办法是反向串: