Flow-Based 理论推导及代码实现
Flow-Based 理论推导及代码实现
在讲Flow-Base之前,需要了解一些数学基础,
- 雅可比矩阵(Jacobian)
- detiminate
数学基础
Flow-based 模型的不同之处
从去年 GLOW 提出之后,我就一直对基于流(flow)的生成模型是如何实现的充满好 奇,但一直没有彻底弄明白,直到最近观看了李宏毅老师的教程之后,很多细节都讲解地比较清楚,就想好好写篇笔记来梳理一下流模型的运作原理。
首先来简单介绍一下流模型,它是一种比较独特的生成模型——它选择直接直面生成模型的概率计算,也就是把分布转换的积分式 p G ( x ) = ∫ z p ( x ∣ z ) p ( z ) d z p_G(x)=\int_z p(x \mid z) p(z) d z pG(x)=∫zp(x∣z)p(z)dz给硬算出来。
要知道现阶段其他较火的生成模型,要么采用优化上界或采用对抗训练的方式去避开概率计算,从而寻找近似逼近真实分布的方法,但是流模型选择了一条硬路(主要是通过变换Jacobian 行列式)来求解,在后文会详细介绍。
流模型有一个非常与众不同的特点是,它的转换通常是可逆的。也就是说,流模型不仅能找到从 A 分布变化到 B 分布的网络通路,并且该通路也能让 B 变化到 A,简言之流模型找到的是一条 A、B 分布间的双工通路。当然,这样的可逆性是具有代价的——A、B 的
数据维度必须是一致的。
A、B 分布间的转换并不是轻易能做到的,流模型为实现这一点经历了三个步骤:最初的 NICE 实现了从 A 分布到高斯分布的可逆求解;后来 RealNVP 实现了从 A 分布到条件非高斯分布的可逆求解;而最新的 GLOW,实现了从 A 分布到 B 分布的可逆求解,其中 B 分 布可以是与 A 分布同样复杂的分布,这意味着给定两堆图片,GLOW 能够实现这两堆图片间的任意转换。
Flow-based Model 的建模思维
首先来回顾一下生成模型要解决的问题:

如上图所示,给定两组数据 z z z 和 x x x,其中 z 服从已知的简单先验分布π(z)(通常是高斯分布),x 服从复杂的分布 p(x)(即训练数据代表的分布),现在我们想要找到一个变换函数f,它能建立一种 z 到 x 的映射f: z → x,使得每对于π(z)中的一个采样点′,都能在 p(x)中有一个(新)样本点′与之对应。
如果这个变换函数能找到的话,那么我们就实现了一个生成模型的构造。因为,p(x)中的每一个样本点都代表一张具体的图片,如果我们希望机器画出新图片的话,只需要从π(z)中随机采样一个点,然后通过f: z → x,得到新样本点 x,也就是对应的生成的具体图片。所以,接下来的关键在于,这个变换函数 f 如何找呢?我们先来看一个最简单的例子。

如上图所示,假设 z 和 x 都是一维分布,其中 z 满足简单的均匀分布:π(z) = 1 (z ∈ [0,1]),x 也满足简单均匀分布:p(x) = 0.5 (x ∈ [1,3])。

那么构建 z 与 x 之间的变换关系只需要构造一个线性函数即可:x=f(z)=2z+1。
下面再考虑非均匀分布的更复杂的情况:
如上图所示,π(z)与 p(x)都是较为复杂的分布,为了实现二者的转化,我们可以考虑在很短的间隔上将二者视为简单均匀分布,然后应用前边方法计算小段上的f∆,最后将每个小 段变换累加起来(每个小段实际对应一个采样样本)就得到最终的完整变换式 f。

如上图所示,假设在[′,′+∆]上π(z)近似服从均匀分布,在[x′,x′+∆x]上 p(x)也近似服从均匀分布,于是有(′ )∆=(′ )∆(因为变换前后的面积/即采样概率是一致的),当∆x 与 ∆极小时,有:

又考虑到 d z d x \frac{dz}{dx} dxdz有可能是负值(如下图所示),而 p ( x ′ ) p(x^′) p(x′)与 π ( z ′ ) \pi(z^′) π(z′)都为非负,所以 p ( x ′ ) p(x^′) p(x′)与 π ( z ′ ) \pi(z^′) π(z′)的实际关系为: p ( x ′ ) = π ( z ′ ) ∣ d z d x ∣ p(x') = \pi (z') | \frac{dz}{dx}| p(x′)=π(z′)∣dxdz∣。

下面进一步地做推广,我们考虑 z 与 x 都是二维分布的情形。

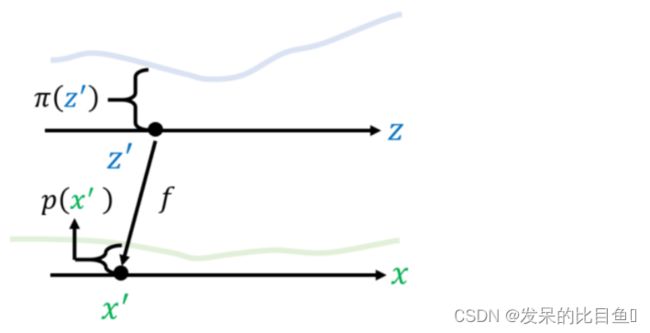
如上图所示,z 与 x 都是二维分布,左图中浅蓝色区域表示初始点′在1方向上移动Δ1,在2方向上移动Δ2所形成的区域,这一区域通过f: z → x映射,形成右图所示 x 域上的浅绿色菱形区域。其中,二维分布π(z)与 p(x)均服从简单均匀分布,其高度在图中未画出(垂直纸面向外)。
因为蓝色区域与绿色区域具有相同的体积,所以有:
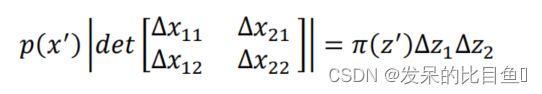
其中 d e t [ Δ x 11 Δ x 21 Δ x 12 Δ x 22 ] det\begin{bmatrix} \Delta x_{11} \Delta x_{21} \\ \Delta x_{12} \Delta x_{22} \end{bmatrix} det[Δx11Δx21Δx12Δx22]代表行列式计算,它的计算结果等于上图中浅绿色区域的面积, 下面我们将∆1∆2移至左侧,得到

即:
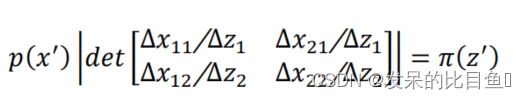
在∆1,∆2很小时,有:
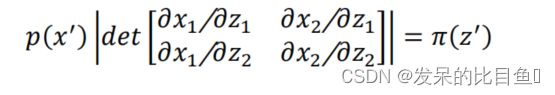
即:
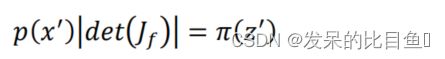
其中表示 f 运算的雅各比行列式,根据雅各比行列式的逆运算,我们得到:
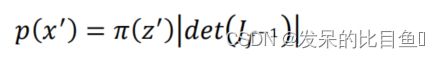
其中−1代表从 x 变换为 z 的变换式,即: z = f − 1 ( x ) z=f^{-1}(x) z=f−1(x)
至此,我们得到了一个比较重要的结论:如果 z 与 x 分别满足两种分布,并且 z 通过函数 f 能够转变为 x,那么 z 与 x 中的任意一组对应采样点′与′之间的关系为

那么基于这一结论,再带回到生成模型要解决的问题当中,我们就得到了 Flow-based Model(流模型)的初步建模思维。

如上图所示,为了实现 z π ( z ) z~\pi(z) z π(z)到 x = G ( z ) ∼ p G ( x ) x = G(z) \sim p_G(x) x=G(z)∼pG(x)间的转化,待求解的生成器 G 的表达式为:
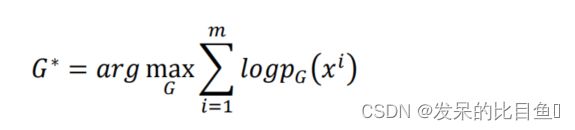
基于前面推导,我们有(x)中的样本点与(z)中的样本点间的关系为:
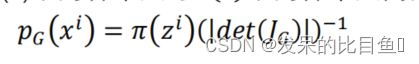
其中 z i = G − 1 ( x i ) z^i = G^{−1}(x^i) zi=G−1(xi)。
所以,如果∗的目标式能够通过上述关系式求解出来,那么我们就实现了一个完整的生成模型的求解。Flow-based Model 就是基于这一思维进行理论推导和模型构建,下面将会详细解释 Flow-based Model 的求解过程。
Flow-based Model 的理论推导&架构设计
上一章中引出的式子:
p G ( x i ) = π ( z i ) ( ∣ d e t ( J G ) ∣ ) − 1 , z i = G − 1 ( x i ) p_G(x^i)=\pi(z^i)(|det(J_G)|)^{-1},z^i=G^{-1}(x^i) pG(xi)=π(zi)(∣det(JG)∣)−1,zi=G−1(xi)
将其取 log,得到:
l o g p G ( x i ) = l o g π ( G − 1 ( x i ) ) + l o g ∣ d e t ( J G − 1 ) ∣ logp_G(x^i) = log \pi(G^{−1}(x^i)) + log| det(JG^{−1})| logpG(xi)=logπ(G−1(xi))+log∣det(JG−1)∣
现在,如果想直接求解这个式子有两方面的困难。第一个困难是, d e t ( J G − 1 ) det(JG^{-1}) det(JG−1)是不好计算的——由于 G − 1 G^{−1} G−1的 Jacobian 矩阵一般维度不低(譬如 256*256 矩阵),其行列式的计算量是
异常巨大的,所以在实际计算中,我们必须对 G − 1 G^{−1} G−1的 Jacobian 行列式做一定优化,使其能够在计算上变得简洁高效。第二个困难是,表达式中出现了 G − 1 G^{−1} G−1,这意味着我们要知 G − 1 G^−1 G−1长什么样子,而我们的目标是求 G G G,所以这需要巧妙地设计 G G G 的结构使得 G − 1 G^{−1} G−1也是好计算的。
下面我们来逐步设计 G G G 的结构,首先从最基本的架构开始构思。考虑到 G − 1 G^{−1} G−1必须是存在
的且能被算出,这意味着 G G G 的输入和输出的维度必须是一致的并且 G G G 的行列式不能为 0。
然后,既然 G − 1 G^{−1} G−1可以计算出来,而 log p G ( x i ) \log p_G(x^i) logpG(xi)的目标表达式只与 G − 1 G^{−1} G−1有关,所以在实际训练中我们可以训练 G − 1 G^{−1} G−1对应的网络,然后想办法算出 G G G 来并且在测试时改用 G G G 做图像生成。

如上图所示,在训练时我们从真实分布 p d a t a ( x ) p_{data(x)} pdata(x)中采样出 x i x^i xi,然后去训练 G − 1 G^{−1} G−1,使得通过 G − 1 G^{−1} G−1生成的 z i = G − 1 ( x i ) z^i = G^{−1}(x^i) zi=G−1(xi)满足特定的先验分布;接下来在测试时,我们从 z z z 中采样出一个点 z j z^j zj,然后通过 G G G 生成的样本 x j = G ( z j ) x^j = G(z^j) xj=G(zj)就是新的生成图像。
接下来开始具体考虑 G G G 的内部设计,为了让 G − 1 G^{−1} G−1可以计算并且 G 的 Jacobian 行列式也
易于计算,Flow-based Model 采用了一种称为耦合层(Coupling Layer)的设计来实现。

代码
# -*- encoding: utf-8 -*-
'''
Filename :NICE.py
Description :
Time :2022/08/01 10:27:10
Author :daiyizheng
Email :[email protected]
Version :1.0
'''
import torch
import torch.nn as nn
from torch.utils.data import DataLoader
from tqdm import tqdm
import matplotlib.pyplot as plt
from torchvision import datasets, transforms
from torch.distributions.transformed_distribution import TransformedDistribution
from torch.distributions.uniform import Uniform
from torch.distributions.transforms import SigmoidTransform
from torch.distributions.transforms import AffineTransform
torch.manual_seed(0)
train_data = datasets.MNIST("./datasets/",
download=True,
train=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize([0.5], [0.5]),
]))
test_data = datasets.MNIST('./datasets/',
train=False,
download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize([0.5], [0.5]),
]))
class StandardLogisticDistribution:
def __init__(self, data_dim=28 * 28, device='cpu'):
self.m = TransformedDistribution(
Uniform(torch.zeros(data_dim, device=device),
torch.ones(data_dim, device=device)),
[SigmoidTransform().inv, AffineTransform(torch.zeros(data_dim, device=device),
torch.ones(data_dim, device=device))]
)
def log_pdf(self, z):
return self.m.log_prob(z).sum(dim=1)
def sample(self):
return self.m.sample()
class NICE(nn.Module):
def __init__(self, data_dim=28 * 28, hidden_dim=1000):
super().__init__()
self.m = torch.nn.ModuleList([nn.Sequential(
nn.Linear(data_dim // 2, hidden_dim), nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim), nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim), nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim), nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim), nn.ReLU(),
nn.Linear(hidden_dim, data_dim // 2), ) for i in range(4)])
self.s = torch.nn.Parameter(torch.randn(data_dim))
def forward(self, x):
x = x.clone()
for i in range(len(self.m)):
x_i1 = x[:, ::2] if (i % 2) == 0 else x[:, 1::2]
x_i2 = x[:, 1::2] if (i % 2) == 0 else x[:, ::2]
h_i1 = x_i1
h_i2 = x_i2 + self.m[i](x_i1)
x = torch.empty(x.shape, device=x.device)
x[:, ::2] = h_i1
x[:, 1::2] = h_i2
z = torch.exp(self.s) * x
log_jacobian = torch.sum(self.s)
return z, log_jacobian
def invert(self, z):
x = z.clone() / torch.exp(self.s)
for i in range(len(self.m) - 1, -1, -1):
h_i1 = x[:, ::2]
h_i2 = x[:, 1::2]
x_i1 = h_i1
x_i2 = h_i2 - self.m[i](x_i1)
x = torch.empty(x.shape, device=x.device)
x[:, ::2] = x_i1 if (i % 2) == 0 else x_i2
x[:, 1::2] = x_i2 if (i % 2) == 0 else x_i1
return x
def training(normalizing_flow, optimizer, dataloader, distribution, nb_epochs=1500, device='cpu'):
training_loss = []
for _ in tqdm(range(nb_epochs)):
for batch, _ in dataloader:
batch = batch.view(-1, 28*28)
z, log_jacobian = normalizing_flow(batch.to(device))
log_likelihood = distribution.log_pdf(z) + log_jacobian
loss = -log_likelihood.sum()
optimizer.zero_grad()
loss.backward()
optimizer.step()
training_loss.append(loss.item())
return training_loss
if __name__ == '__main__':
device = 'cuda'
normalizing_flow = NICE().to(device)
logistic_distribution = StandardLogisticDistribution(device=device)
x = torch.randn(10, 28 * 28, device=device)
assert torch.allclose(normalizing_flow.invert(normalizing_flow(x)[0]), x, rtol=1e-04, atol=1e-06)
optimizer = torch.optim.Adam(normalizing_flow.parameters(), lr=0.0002, weight_decay=0.9)
dataloader = DataLoader(train_data,
batch_size=32,
shuffle=True)
training_loss = training(normalizing_flow,
optimizer,
dataloader,
logistic_distribution,
nb_epochs=500,
device=device)
nb_data = 10
fig, axs = plt.subplots(nb_data, nb_data, figsize=(10, 10))
for i in range(nb_data):
for j in range(nb_data):
x = normalizing_flow.invert(logistic_distribution.sample().unsqueeze(0)).data.cpu().numpy()
axs[i, j].imshow(x.reshape(28, 28).clip(0, 1), cmap='gray')
axs[i, j].set_xticks([])
axs[i, j].set_yticks([])
plt.savefig('Imgs/Generated_MNIST_data.png')
plt.show()
参考
李宏毅老师的教程视频:
https://www.bilibili.com/video/av46561029/?p=59