AcWing 167. 木棒（DFS + 剪枝优化）

一、问题

二、分析

1、整体分析

这道题的数据范围非常小，在这种情况下，大概率就是一道指数级别的算法，即我们的暴力枚举DFS。

这道题中让我们求的是最小长度，所以我们从小开始枚举木棒的长度，利用DFS去暴力枚举看看有没有可能枚举出一种合法的方案。如果可以的话，说明这就是最小长度，如果不可以的话，我们就继续枚举长度。

但我们的长度枚举的时候，只需要枚举所有木棍总和的约数即可。因为只有我们的木棒长度能够整除所有木棍总和的时候，才有可能是答案。

2、剪枝优化

剪枝优化总共分为下面几个方面：
优化搜索顺序，排除等效冗余，可行性剪枝，最优性剪枝，记忆化搜索。

（1）优化搜索顺序

对于一个木棍而言，它要么就是自己再去创造一个新的木棒，要么就接在已有的木棒的后面。每一种选择的背后都是一棵搜索树。选择越多，说明树的节点越多，时间越长。

因此，我们需要减少选择的个数，从而减少搜索树中的子树。所以，我们可以将木棍从大到小排序，从大开始枚举。这样对于我们的一个木棒长度而言，我们的木棍越长，那么留给后续木棍的选择空间就越小。从而减少了后续木棍的选择，进而减少了节点数目。

（2）排除等效冗余

对于一个木棒而言，组成该木棒的木棍之间的顺序是没有要求的，因为这些内部木棍之间的顺序变化并不会一引起木棒长度的变化。

也就是说，我们的DFS中要做的是组合型枚举，而不是排列型枚举。

那么什么是组合型枚举和排列型枚举呢？不懂得同学可以去看一下作者之前得文章：

三类最基础的DFS问题

（3）可行性剪枝

这里先给出结论，在某个新的木棒中，在“尝试接入的第一个木棍”的递归分支就返回失败的话，那么就直接判断失败即可，不需要再去更换当前的第一根木棍继续枚举。

为什么呢？

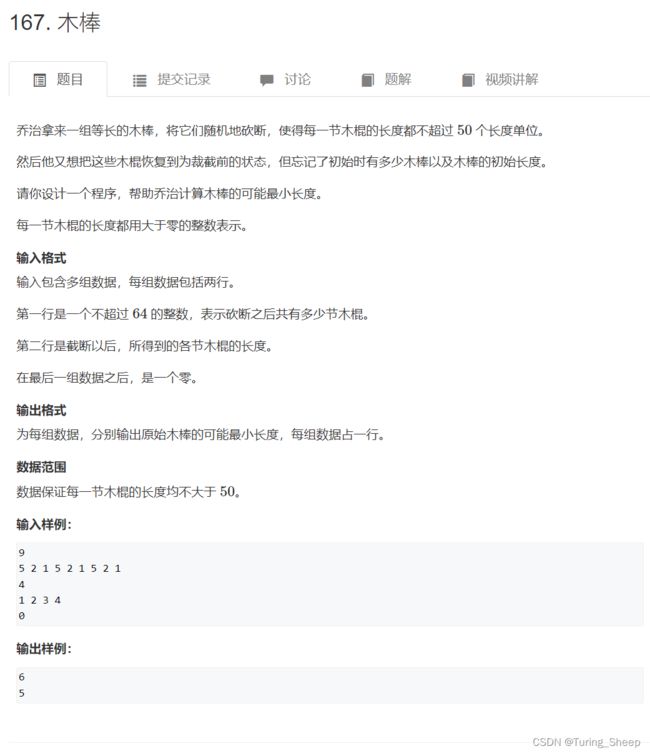
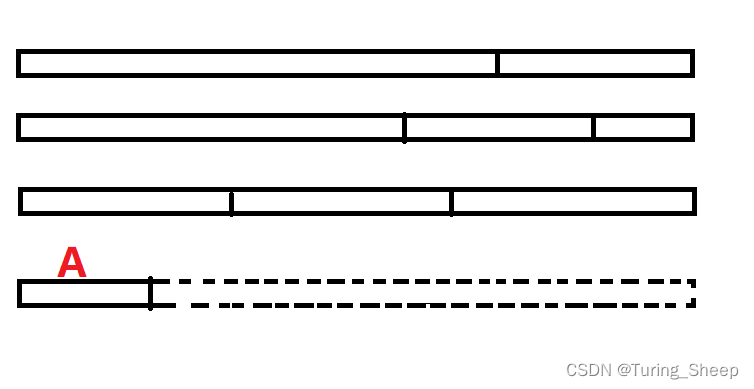
在上面这个图中，我们的第四组新的木棒是我们的目标，我们当前接入了该木棒内的第一根小木棍A，那么为了成功凑出正确长度的木棒。在后续的DFS中，我们就会去利用剩余的小木棍去枚举所有包含木棍A的可能方案。

如果当前分枝返回了失败，意思就是所有利用剩余的小木棍并且包含小木棍A的可能方案都无法凑出一个正确的长度。

由于我们必须用完所有的小木棍，所以我们后续的方案中肯定有一个包含A的方案，但是我们已经知道是不可能了，所以就不用再去枚举后面的方案了。

（4）最优性剪枝

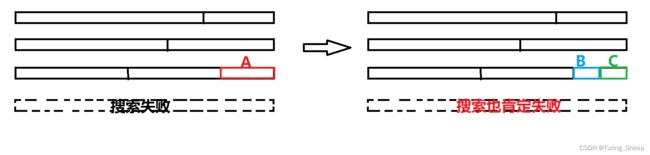
如果当前的木棒在接入最后一根木棒A后，这根木棒的长度恰好满足了条件，但是在拼接剩余木棒的时候失败了。那么回溯后，我们就会更换当前的最后一个木棒A。由于我们木棍的长度是从大到小的，所以用来代替A的必定是更短的多根木棍，假设是B和C。

那么A和B + C是等价的。

也就是说，我们用A的地方，都能用B和C代替。但是，我们用B和C的地方不一定能用A代替，因为我们的A是没法拆分的。也就是说B+C的组合能拼出更多的可能。

那么在结尾是A的时候，我们利用B和C加剩余木棍都没能拼好，那么现在用A和剩余木棍也一定不会拼好。

（5）其他优化

如果一个长度在当前木棒中无法组成正确的长度的话，那么后续和当前长度相同的木棍也不会构成正确的长度，所以直接略掉即可。

三、代码

#include
using namespace std;
const int N = 70;

int n;
int w[N];
int sum, length;
bool st[N];

bool dfs(int u, int cur, int start)
{
    if (u * length == sum) return true;
    if (cur == length) return dfs(u + 1, 0, 0);

    for (int i = start; i < n; i ++ )
    {
        if (st[i] || cur + w[i] > length) continue;

        st[i] = true;
        if (dfs(u, cur + w[i], i + 1)) return true;
        st[i] = false;

        if (!cur || cur + w[i] == length) return false;

        int j = i;
        while (j < n && w[j] == w[i]) j ++ ;
        i = j - 1;
    }

    return false;
}

int main()
{
    while (cin >> n, n)
    {
        memset(st, 0, sizeof st);
        sum = 0;

        for (int i = 0; i < n; i ++ )
        {
            cin >> w[i];
            sum += w[i];
        }

        sort(w, w + n);
        reverse(w, w + n);

        length = 1;
        while (true)
        {
            if (sum % length == 0 && dfs(0, 0, 0))
            {
                cout << length << endl;
                break;
            }
            length ++ ;
        }
    }

    return 0;
}