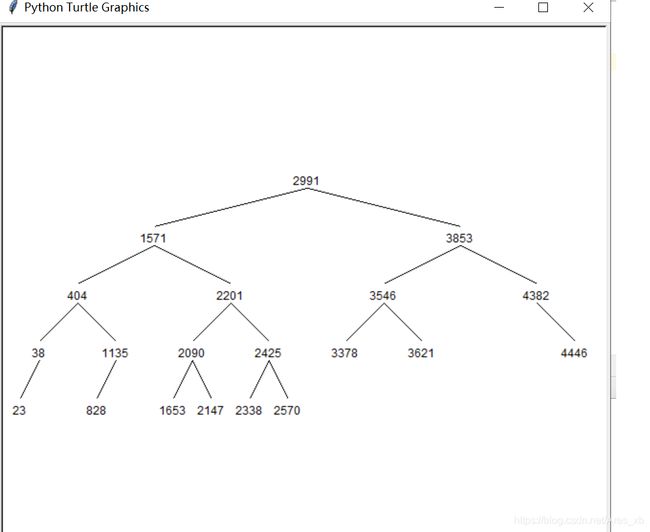
二叉树可视化

#! /usr/bin/env python
# -*- coding: utf-8 -*-


'''
画二叉树
'''


from tree import ergodic_calculate
import turtle

class TreeNode:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

    def __repr__(self):
        return 'TreeNode({})'.format(self.val)


def deserialize(string):
    if string == '{}':
        return None
    nodes = [None if val == 'null' else TreeNode(int(val))
             for val in string.strip('[]{}').split(',')]
    kids = nodes[::-1]
    root = kids.pop()
    for node in nodes:
        if node:
            if kids: node.left = kids.pop()
            if kids: node.right = kids.pop()
    return root


def drawtree(root):
    def height(root):
        return 1 + max(height(root.left), height(root.right)) if root else -1

    def jumpto(x, y):
        t.penup()
        t.goto(x, y)
        t.pendown()

    def draw(node, x, y, dx):
        if node:
            t.goto(x, y)
            jumpto(x, y - 20)
            t.write(node.data, align='center', font=('Arial', 9, 'normal'))
            draw(node.left, x - dx, y - 60, dx / 2)
            jumpto(x, y - 20)
            draw(node.right, x + dx, y - 60, dx / 2)

    t = turtle.Turtle()
    t.speed(0);
    turtle.delay(0)
    h = height(root)
    jumpto(0, 30 * h)
    draw(root, 0, 30 * h, 40 * h)
    t.hideturtle()
    turtle.mainloop()


if __name__ == '__main__':
    pre_list = [1571, 355, 38, 23, 104, 828, 670, 404, 810, 1135, 1072, 2991, 2425, 2090, 1656, 1653, 2201, 2147, 2338,
                2570, 2504, 2887, 4012, 3621, 3378, 3183, 3546, 3853, 4382, 4446]
    pre_list = [2991, 1571, 404, 38, 23, 1135, 828, 2201, 2090, 1653, 2147, 2425, 2338, 2570, 3853, 3546, 3378, 3621,
                4382, 4446]
    inorder_list = [23, 38, 104, 355, 404, 670, 810, 828, 1072, 1135, 1571, 1653, 1656, 2090, 2147, 2201, 2338, 2425,
                    2504, 2570, 2887, 2991, 3183, 3378, 3546, 3621, 3853, 4012, 4382, 4446]
    inorder_list = [23, 38, 404, 828, 1135, 1571, 1653, 2090, 2147, 2201, 2338, 2425, 2570, 2991, 3378, 3546, 3621,
                    3853, 4382, 4446]

    root = ergodic_calculate.construct_tree(pre_list, inorder_list, "postorder")
    # root = ergodic_calculate.construct_tree(pre_list, postorder_list, "inorder_travel")
    drawtree(root)

在复习ALV的时候发现测试的时候整个树的旋转不够直观, 对生成的二叉树的节点位置也不够具体，故此简单写了个小程序可以根据根节点打印整颗二叉树, 可结合上篇博文输入任意两种序列打印整颗二叉树

效果图如下: 

另赋上根据前序中序后序遍历构造二叉树的代码

#! /usr/bin/env python
# -*- coding: utf-8 -*-

'''
遍历推算
根据前序+中序/前序+后序/中序+后序重建二叉树
'''

import operator

pre_list_result = []
inorder_list_result = []
postorder_list_result = []


class Node:
    def __init__(self, data, left, right):
        self.data = data
        self.left = left
        self.right = right


def pre_travel(Node):
    if Node:
        # print(Node.data, end=',')
        pre_list_result.append(Node.data)
        pre_travel(Node.left)
        pre_travel(Node.right)


def inorder_travel(Node):
    if Node:
        inorder_travel(Node.left)
        # print(Node.data, end=',')
        inorder_list_result.append(Node.data)
        inorder_travel(Node.right)


def postorder_travel(Node):
    if Node:
        postorder_travel(Node.left)
        postorder_travel(Node.right)
        # print(Node.data, end=',')
        postorder_list_result.append(Node.data)


def construct_tree(order_one, order_two, travel_type):
    # 参数合法性判断
    if len(order_one) == 0 | len(order_two) == 0:
        return None
    # 参数为前序和中序, 用来求后序
    if "postorder" == travel_type:
        # 前序遍历的第一个结点一定是根结点
        root_data = order_one[0]
        L = order_two.index(root_data)
        # 递归构造左子树和右子树
        left = construct_tree(order_one[1: 1 + L], order_two[:L], "postorder")
        right = construct_tree(order_one[1 + L:], order_two[L + 1:], "postorder")
        return Node(root_data, left, right)
    # 参数为前序和后序, 用来求中序
    elif "inorder_travel" == travel_type:
        if not order_one:
            return None
        root_data = order_one[0]
        if len(order_one) == 1:
            return Node(root_data, None, None)
        L = order_two.index(order_one[1]) + 1
        # 递归构造左子树和右子树
        left = construct_tree(order_one[1: 1 + L], order_two[:L], "inorder_travel")
        right = construct_tree(order_one[1 + L:], order_two[L:-1], "inorder_travel")
        if (L == 1):
            if None != left and left.data > root_data:
                right = Node(left.data, None, None)
                left = None
            if None != right and right.data < root_data:
                left = Node(right.data, None, None)
                right = None
        return Node(root_data, left, right)
    # 参数为中序和后序, 用来求前序
    elif "pre_travel" == travel_type:
        root_data = order_two[-1]
        L = order_one.index(root_data)
        # 递归构造左子树和右子树
        left = construct_tree(order_one[:L], order_two[:L], "pre_travel")
        right = construct_tree(order_one[L + 1:], order_two[L:-1], "pre_travel")

        return Node(root_data, left, right)
    else:
        print("参数错误")


if __name__ == '__main__':
    pre_list = [2169, 1049, 832, 56, 620, 974, 947, 1474, 1473, 1714, 1969, 2552, 2454, 2440, 2510, 3133, 2734, 2885,
                3281, 3632]
    inorder_list = [56, 620, 832, 947, 974, 1049, 1473, 1474, 1714, 1969, 2169, 2440, 2454, 2510, 2552, 2734, 2885,
                    3133, 3281, 3632]
    postorder_list = [620, 56, 947, 974, 832, 1473, 1969, 1714, 1474, 1049, 2440, 2510, 2454, 2885, 2734, 3632, 3281,
                      3133, 2552, 2169]
    # root = construct_tree(pre_list, inorder_list, "postorder")
    # postorder_travel(root)
    # print(postorder_list_result)
    # print(operator.eq(postorder_list,postorder_list_result))

    root = construct_tree(pre_list, postorder_list, "inorder_travel")
    inorder_travel(root)
    print(inorder_list_result)
    print(operator.eq(inorder_list, inorder_list_result))

    # root = construct_tree(inorder_list, postorder_list, "pre_travel")
    # pre_travel(root)
    # print(pre_list_result)
    # print(operator.eq(pre_list, pre_list_result))