数据结构——二叉树四种遍历的实现
目录
一、树的概念
1、树的定义
1)树
2)空树
3)子树
2、结点的定义
1)根结点
2)叶子结点
3)内部结点
3、结点间关系
1)孩子结点
2)父结点
3)兄弟结点
4、树的深度
5、森林的定义
二、二叉树的概念
1、二叉树的性质
2、特殊二叉树
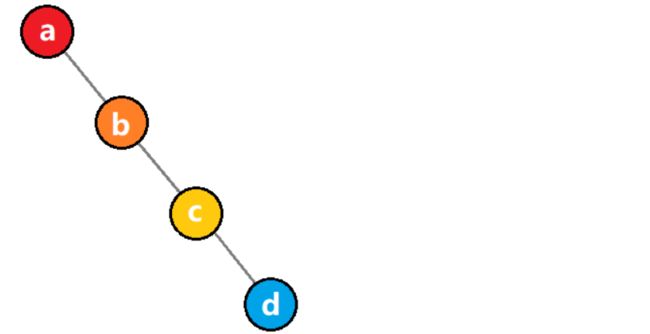
1)斜树
2)满二叉树
2)完全二叉树
3、二叉树的性质
1)性质1
2)性质2
3)性质3
4)性质4
三、二叉树的存储和创建
1、顺序表存储
1)完全二叉树
2)非完全二叉树
3)稀疏二叉树
2、链表存储
3、二叉树的创建
四、二叉树的遍历
1、 先序遍历
1)算法描述
2)源码详解
2、 中序遍历
1)算法描述
2)源码详解
3、 后序遍历
1)算法描述
2)源码详解
4、 层序遍历
1)算法描述
2)源码详解
5、四种遍历代码整合
一、树的概念
1、树的定义
1)树
树是 n(n≥0) 个结点的有限集合。当 n>0 时,它是一棵非空树,满足如下条件:
1)有且仅有一个特定的结点,称为根结点Root;
2)除根结点外,其余结点分为 m 个互不相交的有限集合 T1、T2、…………、Tm,其中每一个 Ti(1≤i≤m) 又是一棵树,并且为根结点 Root 的子树。如图所示,代表的是一棵以 a 为根结点的树。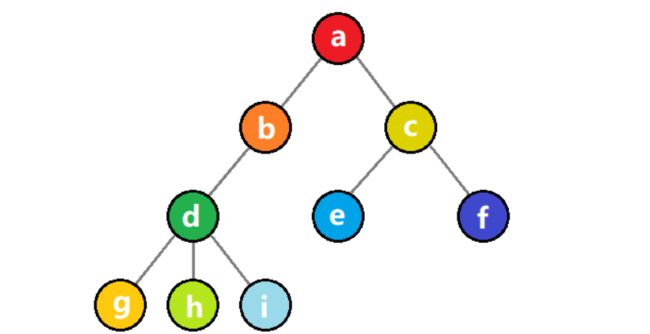
2)空树
当 n=0,也就是 0 个结点的情况也是树,它被称为空树。
3)子树
树的定义用到了递归的思想。即树的定义中还是用到了树的概念,如图所示,T1 和 T2 就是结点 a 的子树。结点 d、g、h、i 组成的树又是结点 b 的子树等等。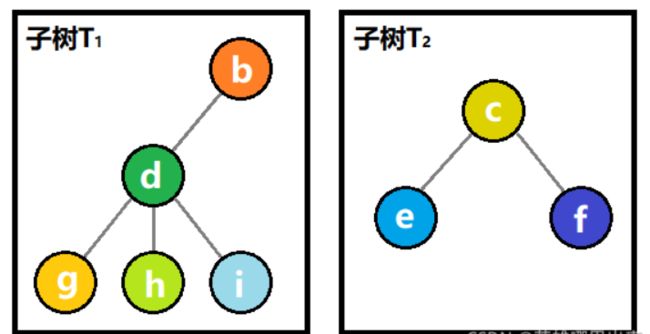
子树的个数没有限制,但是它们一定是互不相交的,如下图所示的就不是树。因为在这两个图中,a 的子树都有相交的边。
2、结点的定义
树的结点包含一个 数据域 和 m 个 指针域 用来指向它的子树。结点的种类分为:根结点、叶子结点、内部结点。结点拥有子树的个数被称为 结点的度。树中各个结点度的最大值被称为 树的度。
1)根结点
一棵树的根结点只有一个。
2)叶子结点
度为 0 的结点被称为 叶子结点 或者 终端结点。叶子结点的不指向任何子树。
3)内部结点
除了根结点和叶子结点以外的结点,被称为内部结点。
如上图所示,红色结点 为根结点,蓝色结点 为内部结点,黄色结点 为叶子结点。
3、结点间关系
1)孩子结点
对于某个结点,它的子树的根结点,被称为该结点的 孩子结点。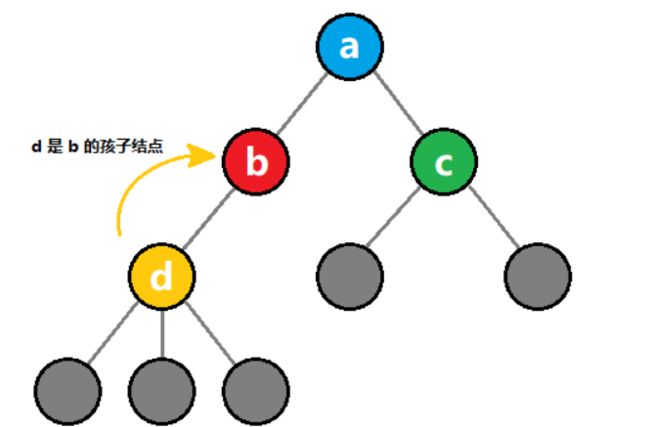
如上图所示,黄色结点 d 是 红色结点 b 的孩子结点。
2)父结点
而该结点被称为孩子结点的 父结点。
如上图所示,蓝色结点 a 是 红色结点 b 的父结点。
3)兄弟结点
同一父结点下的孩子结点,互相称为 兄弟结点。
如上图所示,绿色结点 c 和 红色结点 b 互为兄弟结点。
4、树的深度
结点的层次从根结点开始记为第 1 层,如果某结点在第 i 层,则它的子树的根结点就在第i+1 层,树中结点的最大层次称为 树的深度。
如下图所示,代表的是一棵深度为 4 的树。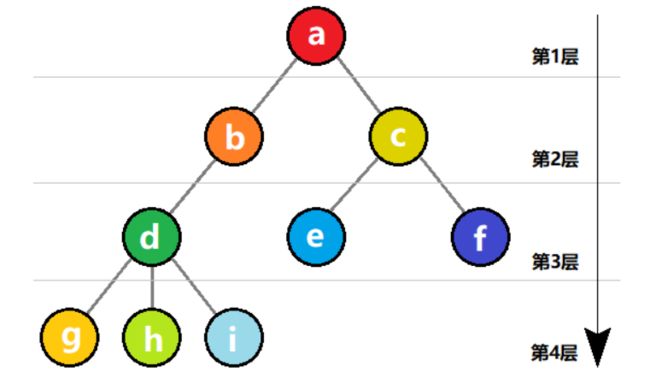
5、森林的定义
森林是 m 棵 互不相交的树的集合,对于树的每个结点而言,其子树集合就是森林。
如图所示,b 和 c 两棵子树组成的集合就是一个森林。
二、二叉树的概念
1、二叉树的性质
二叉树是一种树,它有如下几个特征:
1)每个结点最多 2 棵子树,即每个结点的孩子结点个数为 0、1、2;
2)这两棵子树是有顺序的,分别叫:左子树 和 右子树;
3)如果只有一棵子树的情况,也需要区分顺序,如图所示:![]()
b 为 a 的左子树;![]()
c 为 a 的右子树;
2、特殊二叉树
1)斜树
斜树有点类似线性表,所以线性表可以理解为一种特殊形式的树。
2)满二叉树
对于一棵二叉树,如果它的所有根结点和内部结点都存在左右子树,且所有叶子结点都在同一层,这样的树就是满二叉树。
满二叉树有如下几个特点:
1)叶子结点一定在最后一层;
2)非叶子结点的度为 2;
3)深度相同的二叉树,满二叉树的结点个数最多,为  (其中 h 代表深度)。
(其中 h 代表深度)。
2)完全二叉树
对一棵具有 n 个结点的二叉树按照层序进行编号,如果编号 i 的结点和同样深度的满二叉树中的编号 i 的结点在二叉树中位置完全相同,则被称为 完全二叉树。
满二叉树一定是完全二叉树,而完全二叉树则不一定是满二叉树。
完全二叉树有如下几个特点:
1)叶子结点只能出现在最下面两层。
2)最下层的叶子结点一定是集中在左边的连续位置;倒数第二层如果有叶子结点,一定集中在右边的连续位置。
3)如果某个结点度为 1,则只有左子树,即 不存在只有右子树 的情况。
4)同样结点数的二叉树,完全二叉树的深度最小。
如下图所示,就不是一棵完全二叉树,因为 5 号结点没有右子树,但是 6 号结点是有左子树的,不满足上述第 2 点。
3、二叉树的性质
接下来我们来看下,二叉树有哪些重要的性质。
1)性质1
既然是至多,就只需要考虑满二叉树的情况,对于满二叉树而言,当前层的结点数是上一层的两倍,第一层的结点数为 1,所以第 i 的结点数可以通过等比数列公式计算出来,为 ![]() 。
。
2)性质2
对于任意一个深度为 h 的二叉树,满二叉树的结点数一定是最多的,所以我们可以拿满二叉树进行计算,它的每一层的结点数为![]() 。
。
利用等比数列求和公式,得到总的结点数为:![]()
3)性质3
【性质3】对于任意一棵二叉树 T,如果叶子结点数为 x0,度为 2 的结点数为 x2,则
x0=x2+1
令 x1 代表度 为 1 的结点数,总的结点数为 n,则有:
n=x0+x1+x2
任意一个结点到它孩子结点的连线我们称为这棵树的一条边,对于任意一个非空树而言,边数等于结点数减一,令边数为 e,则有:
e=n−1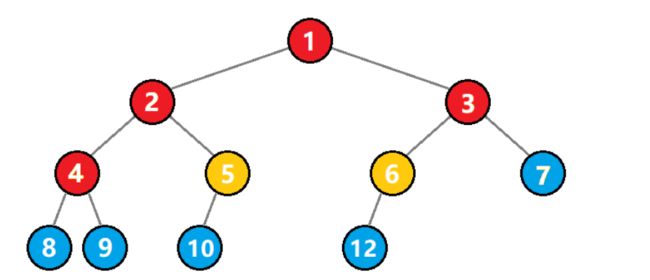
对于度为 1 的结点,可以提供 1 条边,如图中的黄色结点;对于度为 2 的结点,可以提供 2 条边,如图中的红色结点。所以边数又可以通过度为 1 和 2 的结点数计算得出:
e=x1+2x2
联立上述三个等式,得到:
e=n−1=x0+x1+x2−1=x1+2x2
化简后,得证:
x0=x2+1
4)性质4
【性质4】具有 n 个结点的完全二叉树的深度为 [log2n]+1。
由【性质2】可得,深度为 ℎh 的二叉树至多有![]() 个结点。所以,假设一棵树的深度为 h,它的结点数为 n,则必然满足:
个结点。所以,假设一棵树的深度为 h,它的结点数为 n,则必然满足: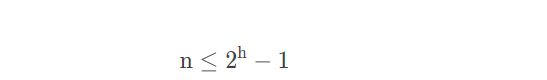
由于是完全二叉树,它一定比深度为 ℎ−1h−1 的结点数要多,即: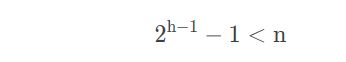
这里,由于 h 一定是整数,所以有:
三、二叉树的存储和创建
1、顺序表存储
二叉树的顺序存储就是指利用数组对二叉树进行存储。结点的存储位置即数组下标,能够体现结点之间的逻辑关系,比如父结点和孩子结点之间的关系,左右兄弟结点之间的关系 等等。
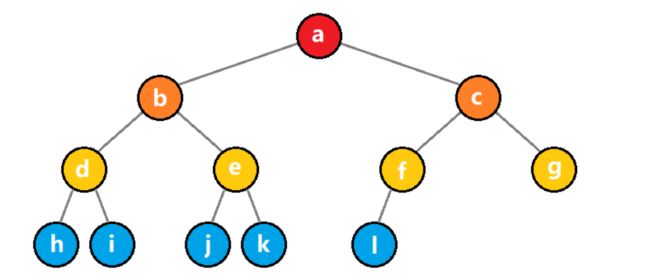
1)完全二叉树
编号代表了数组下标的绝对位置,映射后如下:
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| data | − | a | b | c | d | e | f | g | h | i | j | k | l |
| 这里为了方便,我们把数组下标为 0 的位置给留空了。这样一来,当知道某个结点的下标 x,就可以知道它左右儿子的下标分别为2x 和 2x+1;反之,当知道某个结点的下标 x,也能知道它父结点的下标为 [x / 2] |
2)非完全二叉树
对于非完全二叉树,只需要将对应不存在的结点设置为空即可。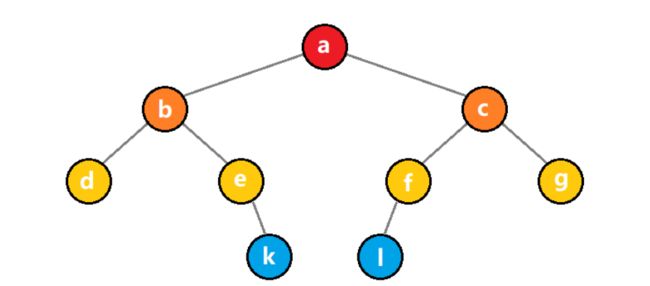
编号代表了数组下标的绝对位置,映射后如下:
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| data | − | a | b | c | d | e | f | g | − | − | − | k | l |
3)稀疏二叉树
对于较为稀疏的二叉树,就会有如下情况出现,这时候如果用这种方式进行存储,就比较浪费内存了。
编号代表了数组下标的绝对位置,映射后如下:
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| data | − | a | b | c | d | − | − | g | h | − | − | − | − |
| 于是,我们可以采取链表进行存储。 |
2、链表存储
二叉树每个结点至多有两个孩子结点,所以对于每个结点,设置一个 数据域 和 两个 指针域 即可,指针域 分别指向 左孩子结点 和 右孩子结点。
typedef char datatype_bt;
typedef struct btreenode{
datatype_bt data;
struct btreenode *lchild; // 指向左孩子节点
struct btreenode *rchild; // 指向右孩子节点
}btree_node,*btree_pnode;3、二叉树的创建
首先创建根节点,接着创建左子树,最后创建右子树,结点不存在输入用#表示
不带形参创建用C语言实现如下:
btree_pnode create_btree(void)
{
btree_pnode t;
datatype_bt ch;
//如果结点不存在,则输入时,用#表示
scanf("%c",&ch);
if('#' == ch)
t = NULL;
else{
//创建根结点
t = (btree_pnode)malloc(sizeof(btree_node));
if(NULL == t){
perror("malloc");
exit(1);
}
t->data = ch;
//创建左子树
t->lchild = create_btree();
//创建右子树
t->rchild = create_btree();
}
return t;
}带形参创建用C语言实现如下:
void create_btree(btree_pnode *T)
{
datatype_bt ch;
//如果结点不存在,则输入时,用#表示
scanf("%c",&ch);
if('#' == ch)
*T = NULL;
else{
//创建根结点
*T = (btree_pnode)malloc(sizeof(btree_node));
if(NULL == *T){
perror("malloc");
exit(1);
}
(*T)->data = ch;
//创建左子树
create_btree(&(*T)->lchild);
//创建右子树
create_btree(&(*T)->rchild);
}
}四、二叉树的遍历
二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中的所有结点,使得每个结点访问一次且仅被访问一次。
对于线性表的遍历,要么从头到尾,要么从尾到头,遍历方式较为单纯,但是树不一样,它的每个结点都有可能有两个孩子结点,所以遍历的顺序面临着不同的选择。
二叉树的常用遍历方法有以下四种:先序遍历、中序遍历、后序遍历、层序遍历。
1、 先序遍历
1)算法描述
【先序遍历】如果二叉树为空,则直接返回。否则,先访问根结点,再递归先序遍历左子树,再递归先序遍历右子树。
先序遍历的结果如下:abdghcefi。
2)源码详解
先序遍历用C语言实现如下:
void pre_order(btree_pnode t)
{
if(t != NULL){
//访问根结点
printf("%c",t->data);
//先序遍历左子树
pre_order(t->lchild);
//先序遍历右子树
pre_order(t->rchild);
}
}扩展:先序非递归算法实现,用到链式栈,可参考如下文章:数据结构——顺序栈与链式栈的实现-CSDN博客
用C语言实现如下:
void unpre_order(btree_pnode t)
{
link_pstack top; //top为指向栈顶结点的指针
init_linkstack(&top); //初始化链栈
while(t != NULL || !isempty_linkstack(top)){
if(t != NULL){
printf("%c",t->data);
if(t->rchild != NULL)
push_linkstack(t->rchild,&top);
t = t->lchild;
}else
pop_linkstack(&t,&top);
}
}2、 中序遍历
1)算法描述
【中序遍历】如果二叉树为空,则直接返回。否则,先递归中序遍历左子树,再访问根结点,再递归中序遍历右子树。
中序遍历的结果如下:gdhbaecif。
2)源码详解
中序遍历用C语言实现如下:
void mid_order(btree_pnode t)
{
if(t != NULL){
//中序遍历左子树
mid_order(t->lchild);
//访问根结点
printf("%c",t->data);
//中序遍历右子树
mid_order(t->rchild);
}
}3、 后序遍历
1)算法描述
【后序遍历】如果二叉树为空,则直接返回。否则,先递归后遍历左子树,再递归后序遍历右子树,再访问根结点。
后序遍历的结果如下:ghdbeifca。
2)源码详解
后序遍历用C语言实现如下:
void post_order(btree_pnode t)
{
if(t != NULL){
//先序遍历左子树
post_order(t->lchild);
//先序遍历右子树
post_order(t->rchild);
//访问根结点
printf("%c",t->data);
}
}4、 层序遍历
1)算法描述
【层序遍历】如果二叉树为空,则直接返回。否则,依次从树的第一层开始,从上至下逐层遍历。在同一层中,按从左到右的顺序对结点逐个访问。
层序遍历需要用到队列知识,可以参考如下文章:
数据结构——顺序队列与链式队列的实现-CSDN博客
2)源码详解
层序遍历用C语言实现如下:
void level_order(btree_pnode t)
{
link_pqueue q;
init_linkqueueu(&q); //初始化链式队列
while(t != NULL){
printf("%c",t->data);
if(t->lchild != NULL)
in_linkqueue(t->lchild,q);
if(t->rchild != NULL)
in_linkqueue(t->rchild,q);
if(is_empty_linkqueue(q))
break;
else
out_linkqueue(&t,q);
}
}5、四种遍历代码整合
btree.h
#ifndef __BTREE_h__
#define __BTREE_h__
#include
#include
#include
typedef char datatype_bt;
typedef struct btreenode{
datatype_bt data;
struct btreenode *lchild,*rchild;
}btree_node,*btree_pnode;
extern void create_btree(btree_pnode *T);
extern void pre_order(btree_pnode t);
extern void unpre_order(btree_pnode t);
extern void mid_order(btree_pnode t);
extern void post_order(btree_pnode t);
extern void level_order(btree_pnode t);
extern void travel(char const *str,void (*pfun)(btree_pnode ),btree_pnode t);
#endif
btree.c
#include "btree.h"
#include "linkqueue.h"
#include "linkstack.h"
#if 0
btree_pnode create_btree(void)
{
btree_pnode t;
datatype_bt ch;
//如果结点不存在,则输入时,用#表示
scanf("%c",&ch);
if('#' == ch)
t = NULL;
else{
//创建根结点
t = (btree_pnode)malloc(sizeof(btree_node));
if(NULL == t){
perror("malloc");
exit(1);
}
t->data = ch;
//创建左子树
t->lchild = create_btree();
//创建右子树
t->rchild = create_btree();
}
return t;
}
#else
void create_btree(btree_pnode *T)
{
datatype_bt ch;
//如果结点不存在,则输入时,用#表示
scanf("%c",&ch);
if('#' == ch)
*T = NULL;
else{
//创建根结点
*T = (btree_pnode)malloc(sizeof(btree_node));
if(NULL == *T){
perror("malloc");
exit(1);
}
(*T)->data = ch;
//创建左子树
create_btree(&(*T)->lchild);
//创建右子树
create_btree(&(*T)->rchild);
}
}
#endif
//先序遍历
void pre_order(btree_pnode t)
{
if(t != NULL){
//访问根结点
printf("%c",t->data);
//先序遍历左子树
pre_order(t->lchild);
//先序遍历右子树
pre_order(t->rchild);
}
}
//先序非递归算法实现
void unpre_order(btree_pnode t)
{
link_pstack top; //top为指向栈顶结点的指针
init_linkstack(&top); //初始化链栈
while(t != NULL || !isempty_linkstack(top)){
if(t != NULL){
printf("%c",t->data);
if(t->rchild != NULL)
push_linkstack(t->rchild,&top);
t = t->lchild;
}else
pop_linkstack(&t,&top);
}
}
//中序遍历
void mid_order(btree_pnode t)
{
if(t != NULL){
//中序遍历左子树
mid_order(t->lchild);
//访问根结点
printf("%c",t->data);
//中序遍历右子树
mid_order(t->rchild);
}
}
//后序遍历
void post_order(btree_pnode t)
{
if(t != NULL){
//先序遍历左子树
post_order(t->lchild);
//先序遍历右子树
post_order(t->rchild);
//访问根结点
printf("%c",t->data);
}
}
//层序遍历
void level_order(btree_pnode t)
{
link_pqueue q;
init_linkqueueu(&q); //初始化链式队列
while(t != NULL){
printf("%c",t->data);
if(t->lchild != NULL)
in_linkqueue(t->lchild,q);
if(t->rchild != NULL)
in_linkqueue(t->rchild,q);
if(is_empty_linkqueue(q))
break;
else
out_linkqueue(&t,q);
}
}
void travel(char const *str,void (*pfun)(btree_pnode ),btree_pnode t)
{
printf("%s",str);
pfun(t);
printf("\n");
}
linkstack.h
#ifndef __LINKSTACK_H__
#define __LINKSTACK_H__
#include
#include
#include
#include "btree.h"
typedef btree_pnode datatype_ls;
typedef struct linkstack{
datatype_ls data;
struct linkstack *next;
}link_stack,*link_pstack;
extern void init_linkstack(link_pstack *Top);
extern bool push_linkstack(datatype_ls data,link_pstack *Top);
extern bool pop_linkstack(datatype_ls *t,link_pstack *Top);
extern bool isempty_linkstack(link_pstack top);
//extern void show_linkstack(link_pstack top);
#endif
linkstack.c
#include "linkstack.h"
//链栈的初始化
void init_linkstack(link_pstack *Top)
{
*Top = NULL;
}
//入栈
bool push_linkstack(datatype_ls data,link_pstack *Top)
{
link_pstack new;
new = (link_pstack)malloc(sizeof(link_stack));
if(NULL == new){
perror("malloc");
return false;
}
new->data = data;
new->next = *Top;
*Top = new;
return true;
}
//出栈
bool pop_linkstack(datatype_ls *t,link_pstack *Top)
{
link_pstack q;
if(isempty_linkstack(*Top)){
printf("链栈是空的!\n");
return false;
}
//出栈
q = *Top;
*Top = (*Top)->next;
*t = q->data;
free(q);
return true;
}
//判断顺序栈是否空
bool isempty_linkstack(link_pstack top)
{
if(top == NULL)
return true;
else
return false;
}
#if 0
void show_linkstack(link_pstack top)
{
link_pstack p;
for(p = top; p != NULL; p = p->next)
printf("%d\t",p->data);
printf("\n");
}
#endif
linkqueue.h
#ifndef __LINKQUEUE_H__
#define __LINKQUEUE_H__
#include
#include
#include
#include "btree.h"
typedef btree_pnode datatype_lq;
typedef struct listnode{
datatype_lq data;
struct listnode *next;
}list_node,*list_pnode;
typedef struct linkqueue{
list_pnode front,rear;
}link_queue,*link_pqueue;
extern void init_linkqueueu(link_pqueue *Q);
extern bool in_linkqueue(datatype_lq data,link_pqueue q);
extern bool out_linkqueue(datatype_lq *t,link_pqueue q);
extern bool is_empty_linkqueue(link_pqueue q);
//extern void show_linkqueue(link_pqueue q);
#endif
linkqueue.c
#include "linkqueue.h"
void init_linkqueueu(link_pqueue *Q)
{
*Q = (link_pqueue)malloc(sizeof(link_queue));
if(NULL == *Q){
perror("malloc");
exit(1);
}
(*Q)->front = (list_pnode)malloc(sizeof(list_node));
if(NULL == (*Q)->front){
perror("malloc");
exit(1);
}
(*Q)->front->next = NULL;
(*Q)->rear = (*Q)->front;
}
bool in_linkqueue(datatype_lq data,link_pqueue q)
{
list_pnode new;
new = (list_pnode)malloc(sizeof(list_node));
if(NULL == new){
perror("malloc");
return false;
}
new->data = data;
new->next = q->rear->next;
q->rear->next = new;
q->rear = new;
return true;
}
bool out_linkqueue(datatype_lq *t,link_pqueue q)
{
list_pnode p;
if(is_empty_linkqueue(q)){
printf("队列是空的!\n");
return false;
}
p = q->front;
q->front = q->front->next;
*t = q->front->data;
free(p);
return true;
}
bool is_empty_linkqueue(link_pqueue q)
{
if(q->rear == q->front)
return true;
else
return false;
}
#if 0
void show_linkqueue(link_pqueue q)
{
list_pnode p;
for(p = q->front->next;p;p = p->next)
printf("%d\t",p->data);
printf("\n");
}
#endif
test.c
#include "btree.h"
int main(void)
{
btree_pnode t; //定义根结点指针
create_btree(&t); //创建二叉树
travel("先序遍历二叉树:",pre_order,t);
travel("先序非递归遍历二叉树:",unpre_order,t);
travel("中序遍历二叉树:",mid_order,t);
travel("后序遍历二叉树:",post_order,t);
travel("按层遍历二叉树:",level_order,t);
return 0;
}
Makefile
CC = gcc
CFLAGS = -Wall -g -O0
SRC = btree.c test.c linkqueue.c linkstack.c
OBJS = test
$(OBJS):$(SRC)
$(CC) $(CFLAGS) -o $@ $^
clean:
$(RM) $(OBJS) .*.sw?
- -o0"表示优化级别为0,即关闭优化。这将导致生成的可执行文件较大,但是可以方便地进行调试。
- "-g"表示生成调试信息,以便在调试程序时可以查看变量的值、函数的调用栈等信息。
- "-Wall"表示启用所有警告,编译器将会显示所有可能的警告信息,帮助开发人员发现潜在的问题。
$(RM):这是一个Makefile中的变量,用于表示删除命令。它可能被设置为系统中的实际删除命令,例如rm或del。$(OBJS):这是一个Makefile中的变量,表示要删除的目标文件列表。.*.sw?:这是一个通配符表达式,用于匹配以.开头的任意文件名,后跟.sw和一个字符(例如.swp)。这通常用于删除编辑器生成的临时文件。
验证结果: