机器学习期末复习题

1.解释什么是过拟合和欠拟合，怎么降低过拟合

过拟合：在训练集中表现的特别优秀，贴合训练数据的特征，但是没有泛化能力，在新的数据集中无法做出准确的预测。

欠拟合：由于训练模型过于简单没有提取到测试样本的特性，无法拟合被测样本。

过拟合的处理：1.获得更多的训练数据2.降维3.正则化4.集成学习方法

欠拟合的处理：1.添加新特征2.增加模型复杂度3.适当减小正则化系数

2.什么是10次10折交叉验证?为什么要这么设计?

10折交叉验证(10-fold cross validation)，将数据集分成十份，轮流将其中9份做训练1份做验证，10次的结果的均值作为对算法精度的估计，一般还需要进行多次10折交叉验证求均值，例如：10次10折交叉验证，以求更精确一点。这个方法的优势在于，同时重复运用随机产生的子样本进行训练和验证，每次的结果验证一次。

3． 什么是预剪枝和后剪枝?从时间开销、过拟合欠拟合风险，泛化性能等角度来讨论起两

种方式的差异.

·预剪枝(pre-pruning):提前终止某些分支的生长

·后剪枝(post-pruning):生成一棵完全树，再“回头”剪枝

时间开销：

预剪枝：训练时间开销降低，测试时间开销降低

后剪枝：训练时间开销增加，测试时间开销降低

过/欠拟合风险：

预剪枝：过拟合风险降低，欠拟合风险增加

后剪枝：过拟合风险降低，欠拟合风险基本不变

泛化性能：后剪枝通常优于预剪枝

4.什么支持向量?利用KKT条件分析硬间隔支持向量机的解具有稀疏性?

支持向量：在支持向量机（SVM）中，支持向量是指距离超平面最近的一些训练样本点。它们对于定义超平面的位置和方向起着关键作用。

利用KKT条件分析硬间隔支持向量机的解具有稀疏性，是因为大多数样本的拉格朗日乘子为零，只有少数支持向量对最优解和决策函数起作用。

5.简单描述下K-means聚类流程，该聚类算法的优点和缺点。

每个簇以该簇中所有样本点的“均值”表示

Step1:随机选取k个样本点作为簇中心

Step2:将其他样本点根据其与簇中心的距离，划分给最近的簇

Step3:更新各簇的均值向量，将其作为新的簇中心

Step4:若所有簇中心未发生改变，则停止；否则执行Step 2

优点：简单高效、可拓展性、可解释性

缺点：对初始聚类中心点敏感、需要预先指定聚类数量、对异常值和噪声敏感、仅适用于欧氏距离度量

6.什么是维数灾难?缓解维数灾难的两大主流技术分别是什么?

维数灾难(Curse of Dimensionality):通常是指在涉及到向量的计算的问题中，随着维数的增加，计算量呈指数倍增长的一种现象。

缓解维数灾难的技术:特征选取、降维

7.在特征选择中,为什么L1范数能比L2范数获得稀疏解?

 

L1范数是向量各元素的绝对值之和，L2范数是向量各元素的平方和的平方根。

L1范数能产生稀疏解，是因为它的最优解往往在某些轴上为0，而L2范数的最优解往往在所有轴上都不为0。
L1范数能够实现特征选择，是因为它会使得一些不重要的特征的系数变为0，从而剔除掉

8．什么是有监督学习和无监督学习，在数据输入上有什么区别?请简单举例说明

有监督学习是指根据给定的输入-输出对（即带有标签的数据）进行学习的过程，目标是找到一个模型，使得该模型在输入训练样本时能够产生尽可能接近真实标签的输出。而无监督学习是指在没有给定输出标签的情况下，根据输入数据的内在结构和关系进行学习的过程，目标是发现数据的内在结构。

输入数据有标签，则为有监督学习；没标签则为无监督学习。线性回归、神经网络决策树、支持向量机等为有监督学习。聚类和降维为无监督学习。

9.什么是泛化误差和经验误差，是不是越小越好?为什么?

经验误差是指模型在训练集上的误差，又称为训练误差。

泛化误差使指模型在“未来”样本集上的误差。

泛化误差越小越好，因为我们训练模型的目的就是为了通过模型进行一定的预测，预测的越准确越好，对应的就是泛化误差越小越好。

经验误差不是越小越好，因为如果训练误差过小会导致模型过拟合，此时，模型不具备很好的泛化能力。

10．决策树生成的基本流程，其三个停止条件式什么?

基本流程

策略：“分而治之”(divide-and-conquer)自根至叶的递归过程在每个中间结点寻找一个“划分”(split or test)属性

三种停止条件：

(1)当前结点包含的样本全属于同一类别，无需划分；

(2)当前属性集为空，或是所有样本在所有属性上取值相同，无法划分；

(3)当前结点包含的样本集合为空，不能划分.

11.聚类算法的两大性能度量指标是什么?其简单举例说明

聚类性能度量：
聚类算法的两大性能度量指标是内部指标和外部指标。 内部指标是根据聚类结果本身来评价聚类算法的优劣，比如SSE（误差平方和：计算每个样本到其所属簇的中心点的距离平方和（越小越好））、轮廓系数、Calinski-Harabaz系数等。
外部指标是根据聚类结果和已知的参考标准（如真实的类别标签）来比较，从而衡量聚类算法的性能，比如准确率（越高越好）、召回率、F1值等。

12.以PCA为例，维度个数的选定有几种方式?

累计贡献法、交叉验证法、平均方差法、拐点法

13.简单描述下PCA算法流程。

PCA算法流程大致如下：

输入：样本集D={x1，x2，.....,xm}

低维空间维数：d'

过程

1.对所有样本进行中心化

2.计算样本的协方差矩阵

3对协方差矩阵做特征值分解

4.取最大的d'个特征值对应的特征向量组成投影矩阵并输出

14．降维和特征选择的相同和不同之处?

降维和特征选择的相同之处是都可以使数据的维数降低，减少数据复杂性和提高模型性能。但是它们的不同之处是，降维是通过将高维特征空间里的点向一个低维空间投影，新的空间维度低于原特征空间，所以维数减少。而特征选择是通过筛选出最有用的特征，去掉冗余或无关的特征，保持原始特征不变。

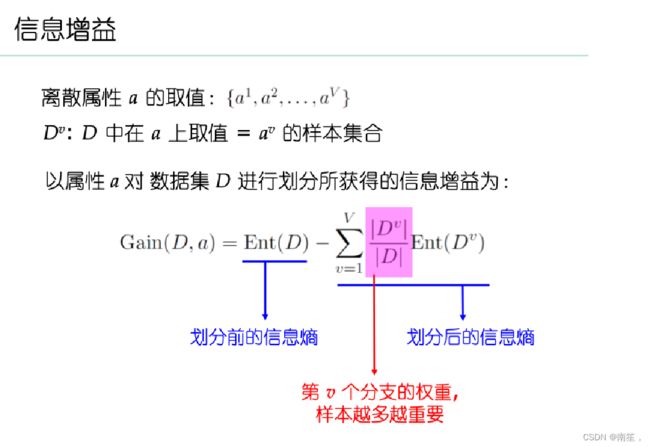
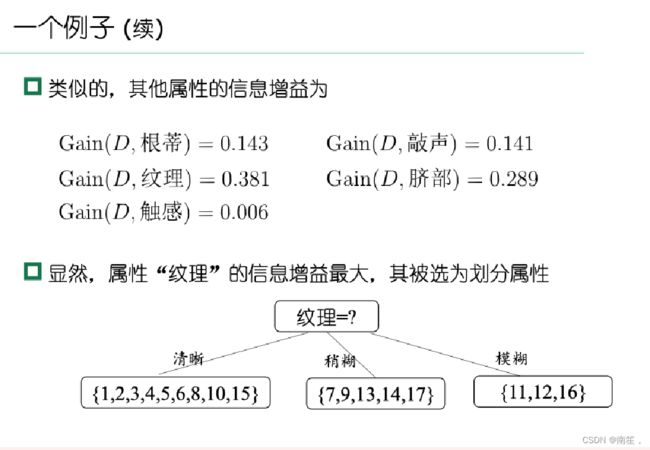
15.(计算题)提供一个西瓜数据集，使用ID3方法计算首个属性节点。

 

16.(计算题)提供一个混淆矩阵，让学生计算查准率和查全率

为了生成混淆矩阵并计算查准率和查全率，我们需要以下步骤：

首先，准备一个分类器对一组样本进行分类。这些样本已经被标记为正类和负类。

创建一个2x2的混淆矩阵。混淆矩阵的行表示实际的类别（真实标签），列表示分类器的预测类别（预测结果）。

对于每个样本，根据其真实标签和分类器的预测结果，将计数加到相应的混淆矩阵单元格中。

混淆矩阵的四个单元格表示了四种情况：

真正例（True Positive，TP）：分类器正确地将样本预测为正类。

假正例（False Positive，FP）：分类器错误地将样本预测为正类。

真反例（True Negative，TN）：分类器正确地将样本预测为负类。

假反例（False Negative，FN）：分类器错误地将样本预测为负类。

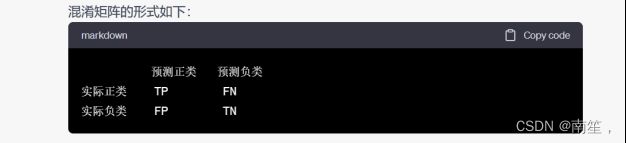
混淆矩阵的形式如下：

 计算查准率（Precision）和查全率（Recall）：

查准率是指在分类器预测为正类的样本中，实际为正类的比例。计算公式为：Precision = TP / (TP + FP)。

查全率是指在实际为正类的样本中，被分类器正确预测为正类的比例。计算公式为：Recall = TP / (TP + FN)。

通过以上步骤，我们可以生成混淆矩阵，并计算相应的查准率和查全率。