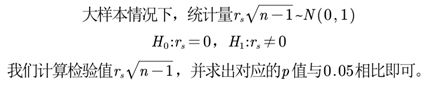数学建模学习笔记之相关系数
最近在同学安利下入手华科老学长清风的数学建模课程,在这里记录下笔记。做笔记的目的主要是将较长的视频精简成短时间能看完的文档,方便日后复习用,也希望能给予后来者一点帮助。
数学建模学习笔记 : 相关系数
- 零、假设检验
- 零、描述性统计
- 一、皮尔逊Person相关系数
- 二、正态性检验
-
- (一)雅克-贝拉检验(Jarque-Bera test) . [ 4 ] .^{[4]} .[4]
- (二)Shapiro-wilk夏皮洛-威尔克检验
- 三、相关性检验 . [ 6 ] .^{[6]} .[6]
- 四、斯皮尔曼Spearman相关系数
-
- Spearman相关系数的相关性检验:
-
- (1)小样本:临界值表法
- (2)大样本
- 补充、代码及软件
给定两个变量X和Y,问它们两个是否具有线性相关性?一般做法是抽取一些样本,然后计算相关系数。
注意:相关性≠因果性。夏天,雪糕销售量高,游泳人数多,雪糕销售量和游泳人数有正相关,但不能说雪糕和游泳有因果关系。
零、假设检验
第一步:作出假设 H 0 H_{0} H0,对应反假设 H 1 H_{1} H1。(又称为原假设与备择假设)
第二步:原假设下,某统计量需服从某个分布。找到常用的分布比较好。
第三步:作出该分布的概率密度图像,并找到该分布下95%的面积覆盖的区域(接受域)。( β = \beta= β= 95%称为置信水平。α=0.05称为显著性水平,用于衡量拒绝有多显著。)如果原假设成立,那么大部分样本都应该落在接受域内。
第四步:取一个样本。若该样本对应的统计量的值不在接受域内,则我们判断原假设不成立,这个判断仅有不超过5%的可能是错的,即有95%的把握拒绝原假设。(严谨语言:在95%的置信水平下拒绝原假设。)反之,如果在接受域内,则在95%的置信水平下不能拒绝原假设(这并不表示有95%的把握接受原假设)。
第四步’:取一个样本,计算其对应的统计量的值z*,记p =
P(X>=z*),若p<0.025(95%置信水平下的双侧检验),则说明落在了接受域外,则拒绝原假设。如果是单侧检验,则判据为p<0.05。也可以认为,如果是双侧检验,则判据为2p<0.05。 . [ 1 ] .^{[1]} .[1]
例题:小明称体重发现自己94斤,而之前都是90斤。
解:原假设:小明没胖。备择假设:小明胖了。
记小明的体重为W,则在原假设下,W应满足 W ∼ N ( 90 , 4 ) W\sim N(90,4) W∼N(90,4) 。(?方差4不知是怎么设的)
即统计量(只包含W一个未知量或待测量) Z = W − 90 2 ∼ N ( 0 , 1 ) Z = \frac{W - 90}{2}\sim N(0,1) Z=2W−90∼N(0,1).
取β=95%,作出概率密度函数和接受域(双侧)

其中1.96可以查表得到,也可以用 F − 1 ( 0.025 + 0.95 ) F^{- 1}(0.025 + 0.95) F−1(0.025+0.95)得到,其中F(x)=P(X<=x)是累积分布函数。[^1]
当取样值W=94时,计算得Z*=2>1.96不在接受域内,故冒5%以下的风险拒绝原假设,或在95%的置信水平下拒绝原假设。也就是说,小明胖了。
这时候,如果增大置信水平(更倾向于相信原假设),比如取β=99%,则对应的接受域为[-2.58,2.58],这个时候就落在接受域内,称在99%的置信水平下不能拒绝原假设(但很显然,这并不代表有99%的把握接受原假设,只是不能冒1%以下的风险拒绝原假设)。
零、描述性统计
一般来说,我们得到一组统计数据的时候,先对这些数据求最小值、最大值、平均值等简单信息的统计计算,这称为描述性统计。 . [ 2 ] .^{[2]} .[2]

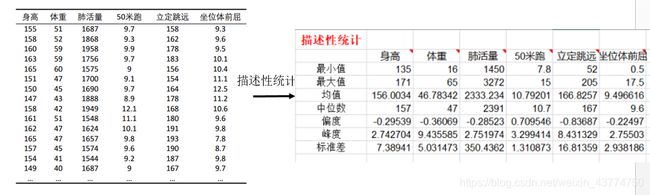
为了看出变量之间的两两关系,可以画出矩阵散点图 plotmatrix(),
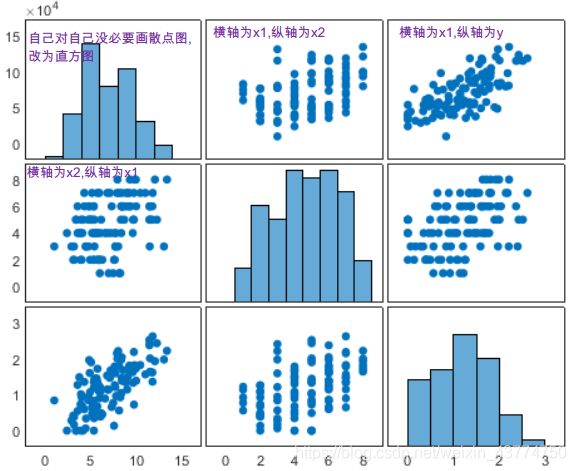 . [ 3 ] .^{[3]} .[3]
. [ 3 ] .^{[3]} .[3]
一、皮尔逊Person相关系数
回到相关系数的话题。比如探讨男生的身高和体重的线性相关性,就找几个男生,测一些他们的身高体重,然后利用下面的公式计算相关系数
 相关系数为1,说明正线性相关;为-1,说明负线性相关;为0,说明无关。
相关系数为1,说明正线性相关;为-1,说明负线性相关;为0,说明无关。
但是,使用相关系数需要注意以下几点
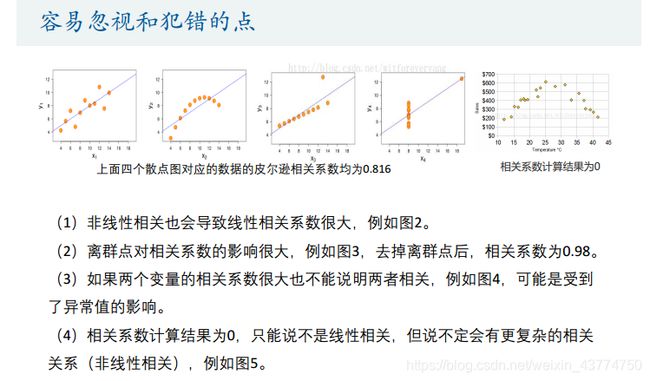 也就是说,只有事先知道了两个变量大致是线性相关的(一般先画散点图看出),才能使用相关系数,否则相关系数无意义。
也就是说,只有事先知道了两个变量大致是线性相关的(一般先画散点图看出),才能使用相关系数,否则相关系数无意义。
数据差异比较大的数据不适合用Person相关系数,因为离群点影响大。
Person相关系数还有一个使用前提:各变量需服从正态分布。(因为之后的相关性检验会用到t分布,而t分布要求数据服从正态分布。)
二、正态性检验
如何检验一个变量是否服从正态分布?
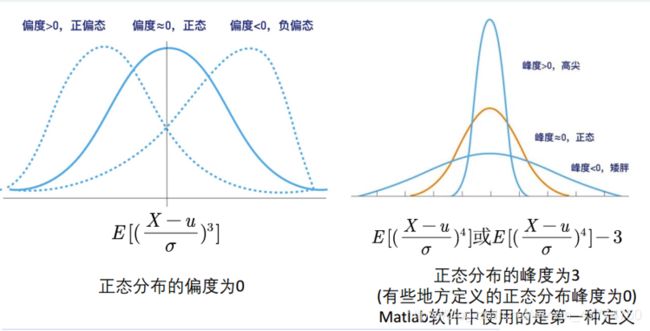
(一)雅克-贝拉检验(Jarque-Bera test) . [ 4 ] .^{[4]} .[4]

其中,n是取样数, 该方法要求n>30。
 已知卡方分布图像,在样本的n、S、K都已知的情况下,就可以计算出p值,即在卡方分布下的P(X>=JB*). . [ 5 ] .^{[5]} .[5]
已知卡方分布图像,在样本的n、S、K都已知的情况下,就可以计算出p值,即在卡方分布下的P(X>=JB*). . [ 5 ] .^{[5]} .[5]
(二)Shapiro-wilk夏皮洛-威尔克检验
适用于小样本(3<=n<=50)。同理,可用SPSS计算出p值(matlab中没有相关代码),如果p值<0.05则拒绝原假设。该检验是基于什么分布的不管了,会用就行。
小技巧:如果检验发现一组样本中某几个变量符合正态分布,某几个不符合,可以只挑其中一两个符合正态分布的写进论文中,其他不提。
三、相关性检验 . [ 6 ] .^{[6]} .[6]
只有通过了正态性检验,才能接着进行相关性检验。
假定我们计算出了两个变量的相关系数是0.4,距离1有点远,但又不完全是0,那这两个变量到底是否相关呢?这实际上与具体变量有关。不同的变量及所采到的样本下,0.4可能表示相关也可能表示不相关,这需要通过相关性检验来看。
假定我们计算出了两变量的相关系数r,想要检验两变量是否相关。
原假设 H 0 H_{0} H0 : r与0相差无几,即两变量不相关。
备择假设 H 1 H_{1} H1 : r与0显著相异,即两变量相关。
在原假设成立的条件下,统计量 t = r n − 2 1 − r 2 ∼ t ( n − 2 ) t = r\sqrt{\frac{n - 2}{1 - r^{2}}}\sim t(n - 2) t=r1−r2n−2∼t(n−2)
分布已知、样本已知,则可以计算p值。若p<0.05,则拒绝原假设,即有95%的把握认为两变量相关。
推广之,通常相关性检验分三阶段:
第一阶段,p<0.10,说明在90%的置信水平下拒绝原假设。
第二阶段,p<0.05,说明在95%的置信水平下拒绝原假设。
第三阶段,p<0.01,说明在99%的置信水平下拒绝原假设。
相关系数旁边打星号可作为显著性标记,0.4*、0.4**、0.4***分别表示通过了第一、二、三阶段的相关性检验。*越多,说明两变量相关的把握越大。
四、斯皮尔曼Spearman相关系数
Person相关系数要求严苛:数值型数据[8],正态分布,线性关系。
以上任一点不满足,就得用Spearman相关系数。
Spearman相关系数可以处理定序数据,还可以处理单调关系(线性函数、指数函数、对数函数)。
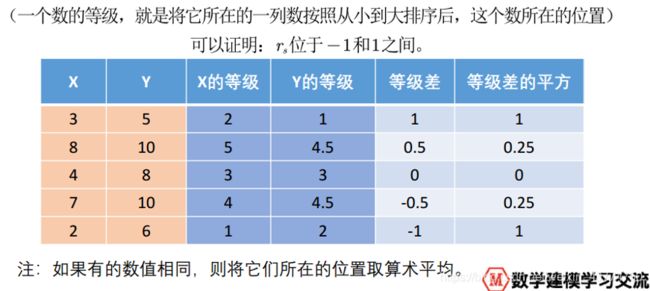
 . [ 9 ] .^{[9]} .[9]
. [ 9 ] .^{[9]} .[9]
还有一种定义是,Spearman相关系数就是两变量取等级化后的皮尔逊相关系数。
Spearman相关系数不需要正态性检验。
Spearman相关系数的相关性检验:
(1)小样本:临界值表法
对于给定的n值和样本计算出来的r值,如果r大于表中对应的值,则认为两变量相关。
(2)大样本
补充、代码及软件
[1]求正态分布的累积分布函数的反函数 1.96 = F − 1 ( 0.025 + 0.95 ) F^{- 1}(0.025 + 0.95) F−1(0.025+0.95) = norminv(0.975).
求正态分布的p值 = 1-normcdf(z*) 双侧检验要乘2
[2]excel、SPSS中也有描述性统计的功能,可直接用。
[3]SPSS可以画出矩阵散点图。本节所说的内容都可以用SPSS直接做出,比如正态性检验的p值表、相关性检验的p值表等。
[5]matlab进行JB检验的代码是 [h,p] = jbtest(x,alpha).其中x是样本列向量,alpha是显著性水平。p就是根据样本和卡方分布计算出来的p值,如果p值 [6]matlab计算相关系数及相关性检验 左边是matlab输出的内容,右边是经过整理、标星号后的相关系数表。 [7]相关系数表的美化 也可以自定义管理规则 [8]数值型数据、定序数据与不定序数据 片尾广告
[R,P] = corrcoef(X,Y)
其中X,Y是两列向量。输出两列向量的相关系数和相关性检验的p值。
[R,P] = corrcoef(Data)
其中Data是由许多列向量组成的矩阵。输出各列向量两两之间的相关系数及相关性检验的p值。
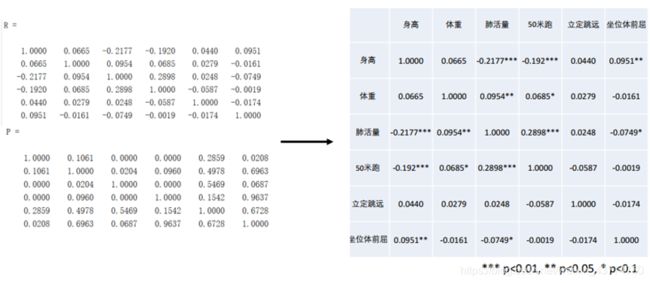
斯皮尔曼相关系数同理,代码换成 [R,P] = corr(Data,‘type’,‘Spearman’) 即可。
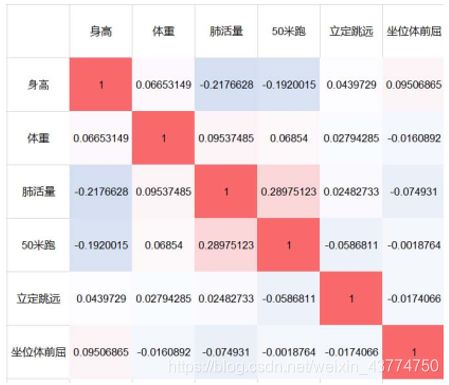
把相关系数表复制到excel中,选中相关系数表,选择条件格式-色阶,可以根据数值大小进行上色。


这样,-1是最蓝,1是最红,0是白色,就可以直观地看出相关系数的大小了。
数值型数据就是有明确数字含义的数据,比如成绩。
定序数据是着重侧重顺序关系的数据,比如成绩排名。
不定序数据是无明确数字含义、也不侧重顺序的数据,比如男、女(可以用数字表示,但无数字含义)。
定序数据可以用Spearman相关系数。
清风数学建模课程,B站上可以免费看前几节,讲的挺好的,还在不断更新。最近更新了许多内容,我还没来得及看,想进一步了解的可以自己去看看。
链接: 清风数学建模课程.