并归排序（底层原理）+求逆序数

1.底层原理

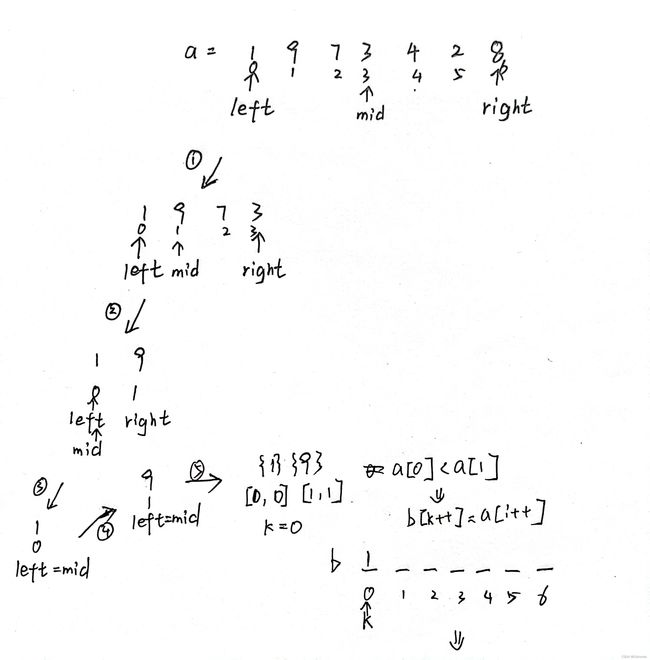
通过把数组拆分成单组元素，相邻两组元素比较最左边的元素大小（将两者较小的元素先放入组中），拼凑成新的组，由于是从单个元素开始组合，这就决定了一个很关键的性质，每组元素都是从左向右单调递增的，及右边的元素一定比左边的任何一个元素大。(归并排序原理)

当左边组某一个元素与右边组某一个元素比较时，左边组这个元素大于右边组这个元素，是不是说明在组内，这个元素的右边所有元素都要大于右边组这个元素。举个例子图中有[1,3,7,9]组和右边[2,3,4,7]组，第一次1小于2，不管它，放到新的组里边，第二次比较3和2,3>2,那么3右边的7和9是不是都要大于2，这时就产生了3组逆序对，由于每两组元素在之前都是分开的，没有碰到过，这确定了，产生逆序对的唯一性，在[i,ie]和[j,je]两组中，只要第左边一组第n个元素大于右边的某个元素，那么就会有ie-n+1个逆序对产生。(找出逆序数原理)

2.实现归并排序和查找逆序数

归并排序

在写代码的过程中，逻辑略有不同。定义一个left表示最左边的元素，定义一个right表示最右边的元素mid=（left+right）/2,先递归把最右边第一个元素划分出来。

我们把函数，mergsort想象成一个机器，投进去1,9,7,3,4,2,8，机器1会先把1,9,7,3交给里面的机器2，然后，机器2又会把1,9交给‘’机器3，然后机器3又会把1交给机器4，这个机器发现1已经是有序的了，它会告诉上面的机器1已经排序完毕，然后，机器3会把9交给机器4，排序完成后该轮到机器3工作了，机器3会把1和9排成[1,9],此时机器2在把右半边的7，3给到机器3，按照以上方式进行处理。这是我们发现了每一个机器会将自己拿到的组分成两块，一块交给机器（左）处理一块交给机器（右）处理，那么我们在递归中便需要递归两次，一个处理左半部分，一个处理右半部分。

接下来我们来写代码。

using i64 = long long;
i64 n,ans;
void mergesort(i64 left, i64 right,std::vector&a, std::vector& b) {
	if (left < right) {
		i64 mid = (left + right) / 2;
		mergesort(left, mid,a,b);
		mergesort(mid + 1, right,a,b);
		
	}
}

signed main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	std::cin >> n;
	std::vectora(n);
	std::vectorb(n);
	for (i64 i = 0; i < n; i++)std::cin >> a[i];
	mergesort(0, n-1,a,b);
	std::cout << ans;
	return 0;
}

我们需要一个容器a来储存要排列的元素，一个容器b来存储每组排列好的元素，按照我们刚才得到的结论，当left=right的时候说明已经分割成一个元素了，就不能再分割了，这时回到上一层，进入if，我们要使用两次递归，一次处理左半部分[left,mid],一次处理右半部分[mid+1，right]，那么按照我们开头写的逻辑，我们需要定义两个区间并使用变量k来指向b容器的第一个位置

i64 i = left, j = mid + 1, ie = mid, je = right,k=0;//[i,ie],[j,je]

分别表示左半组和右半组

接着我们要进行比较，当两组都没有到最右端的时候，分别比较a[i]和a[j],i和j分别是指向两组最左边的元素（没有使用过的），当a[i]<=a[j],b[k]=a[i],此时i和k都要跳到下一个为置，所以为了简洁起见使用b[k++]和a[i++],如果a[i]>a[j],我们将j（右组最左边的元素）放入b[k]中。

while (i <= ie && j <= je) {
	if (a[i] <= a[j])b[k++] = a[i++];
	else {
		b[k++] = a[j++];
	}
}

当其中有一个组被使用完后，显然没有被使用完的一组最左边的元素是大于被使用完的一组的最右边的元素的（举个例子，[1,2,3,4,4],和[4,5,6,7],在比较过程中会出现b=[1,2,3,4,4,4],左边已经使用完了，右边一组剩下的[5,6,7]显然都大于4，我们直接将[5,6,7]都放入b的最有边就好了b=[1,2,3,4,4,4,5,6,7],如果是右边剩余，同理）我们直接将另一组的元素挨个排在b容器后面就行了。

while (i <= ie)b[k++] = a[i++];
while (j <= je)b[k++] = a[j++];

 最后，我们排列好的组重新放回vector a中

for (i64 h = left; h <= right; h++)a[h] = b[h-left];

由于我们b每次都是从k=0开始使用，所以要让它从h-left=0开始放回，left代表的是这一组中最左边的元素在a原来的位置，right代表的是右边。

最后把代码组合起来

using i64 = long long;
i64 n,ans;
void mergesort(i64 left, i64 right,std::vector&a, std::vector& b) {
	if (left < right) {
		i64 mid = (left + right) / 2;
		mergesort(left, mid,a,b);
		mergesort(mid + 1, right,a,b);
		i64 i = left, j = mid + 1, ie = mid, je = right,k=0;//[i,ie],[j,je]
		while (i <= ie && j <= je) {
			if (a[i] <= a[j])b[k++] = a[i++];
			else {
				b[k++] = a[j++];
				ans += ie - i + 1;
			}
		}
		while (i <= ie)b[k++] = a[i++];
		while (j <= je)b[k++] = a[j++];
		for (i64 h = left; h <= right; h++)a[h] = b[h-left];
	}
}

signed main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	std::cin >> n;
	std::vectora(n);
	std::vectorb(n);
	for (i64 i = 0; i < n; i++)std::cin >> a[i];
	mergesort(0, n-1,a,b);
	std::cout << ans;
	return 0;
}

查找逆序数

我定义了一个变量ans，在先前逆序数原理中，我解释了"在[i,ie]和[j,je]两组中，只要第左边一组第n个元素大于右边的某个元素，那么就会有ie-n+1个逆序对产生。"，所以只要在else，即a[i] > a[j]

的情况下，添加上ans+=ie-n+1即可这里的n其实就是i，因为i指向的就是左边一组最左边的元素（没使用过的），所以我们把n改成i，即ans+=ie-i+1就好了。

这篇文章如果对你有帮助，请点个赞吧。