腐蚀膨胀算法、开闭运算原理讲解及完整C语言实现

---

腐蚀与膨胀算法

概念

腐蚀：腐蚀操作可以消除噪点，同时消除部分边界值，导致目标图像整体缩小。
膨胀：膨胀操作可以使目标特征值增大，导致目标图像整体放大。
组合：腐蚀和膨胀组合起来使用，可以达到更好分割独立的图形元素的目的。

核：腐蚀和膨胀算法的灵魂，也是最需要花心思设计的东西，根据目标图像的特征不同，要设置不同的核才能产生很好的效果。更专业的叫法叫做“结构元素”，其中核心，也就是结构元素的中心点，叫做“锚点”，一般采用结构元素的影响区域的最小像素值去替换掉“锚点”的像素值

想像有一板墙画（目标图像），历经岁月，墙上很多岁月的斑驳痕迹，很多色彩掉了，或者有些地方发霉了（噪点），很丑，而你手提着一把油漆刷（核/结构元素），要把这板墙画修复一下，采用什么办法刷呢？就是一行行用油漆刷拉过去。

案例

交集和并集操作

先回忆一下高中数学的交集（符号是∩）和并集（符号是∪）操作：

• 假设有两个不同的数组: A={1,2,3} ; B = {1,6,9} ;
  则 A ∩ B = {1} A ∪ B = {1,2,3,6,9}
• 假设该数组为一个简单的2×2矩阵
  
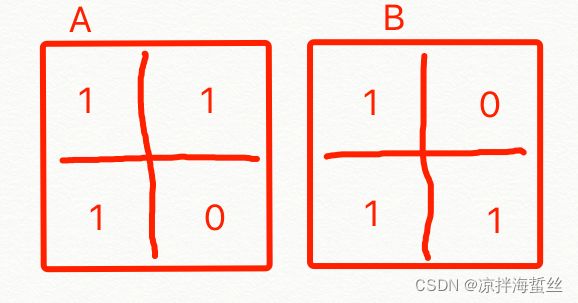
  根据交集∩的操作，必须是AB矩阵相同的部分保留，不同部分排除（设为0)，则得：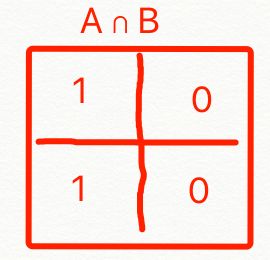
  
  据并集∪的操作，AB两个矩阵全部部分都保留，不做排除，则得：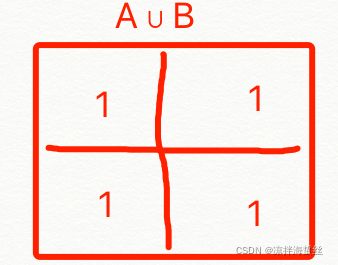
  

案例图片

假设识别了一张99像素的目标图片，得到一组99的RGB三原色通道二维数组，假设只有黑(0,0,0)和白(255,255,255)两种颜色，如下图所示：

我们人眼跟着W（white)的点走，虽然左上角，左下角和右下角有一些噪点，但还是很容易就辨认出来是个2，怎么让2看起来更加显眼呢？这个时候就是我们的腐蚀与膨胀算法开始干活了。我们定义一个“核”，你可以简单把它理解为“刷子”“模版”，像刷油漆一样，一下下往目标图中刷。

腐蚀

腐蚀的规则就是：选择一个核，核中1的区域如果有W（白色），则把核的中心那个点标注为W，如果1的区域没有W，则不用处理，这里相当于“&&”且运算

“十”形核

刷油漆开始：

第一次，可以看到十字型区域没有W白点，所以核心点不需要更改颜色。

第二次，发现十字形区域有W白点，则核心点颜色要改成白色，这里我用W+表示，涂漆后就会出现

继续往下刷，如果颜色本来就是W的就不需要改每一行都要刷过去，刷完后的结果：

可以发现黑色底色被腐蚀缩小，白色目标区域被放大，但是图像一塌糊涂，根本不是我们想要的。
这个时候，我们就该考虑更换核，也就是换把“刷子”。

“三角形”核

第一步：

第二步：

开始不停递归，涂漆完成后：
可以看到，三角形核的腐蚀效果更好，起码比十字形的好，当然这里也是简单例子做个展示，总结一下主要有两点：
（1) 不同图像使用不同核的腐蚀效果不同
（2) 腐蚀通过平移和&判断，增大目标图像的特征，缩小黑色背景色的影响

膨胀

膨胀其实非常类似，只不过它关注的是核形状区域有没有黑色B，如果有，就把锚点涂成黑色
假设膨胀的核也是小三角，用同样的核去针对上面腐蚀后的图像做膨胀，我们看看会发生什么：
第一步：发现本来就是B，不需要修改

第二步：发现有B，则把该W+的锚点改成黑色

继续刷下去，然后得出膨胀后的结果：

发现原来胖胖的2，变得非常瘦了，甚至下面那一横都被当成是噪点消没了，当然实际情况中，目标图像的像素值不可能只有可怜巴巴的一行N列，所以肯定不会被完全消除的，最多就是被瘦身，而一些较小的噪点，则会被消除。
原来黑色底区域，膨胀大了。

这就是腐蚀与膨胀的底层实现逻辑，当然我如果使用不同的核，膨胀结果也会不同，具体还是要多试几种，根据实际情况决定。

开闭运算

设目标图像为X，腐蚀为E，膨胀为D。

开运算

先腐蚀，后膨胀，称之为：开运算（OPEN(X) = D(E(X))
通过开运算，能够去除孤立的小噪点，图形中的毛刺，两区域间小桥，而整体图形大体上不变

闭运算

先膨胀，后腐蚀，称之为：闭运算（CLOSE(X) = E(D(X))）
通过闭运算，可以修复主体图形中的坑坑洼洼，填补小裂缝，使其目标特征更加完备

代码实现

不使用CV库的C语言代码实现

结构元

类型定义

typedef struct
{
	int* x;  // 值为1的元素行坐标
	int* y;  // 值为1的元素列坐标
	int len;  // 值为1的元素数量
}StrElem;

自定义结构元

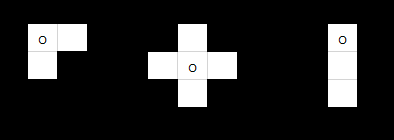
如上图结构元，参数分别为：

StrElem se1，se2, se3;
se1.x = {0, 0, 1};
se1.y = {0, 1, 0};
se1.len =3;

se2.x = {-1, 0, 0, 0, 1};
se2.y = {0, -1, 0, 1, 0};
se2.len = 5;

se3.x = {0, 1, 2};
se3.y = {0, 0, 0};
se3.len = 3;

标准结构元

标准结构元直接输入参数来调用，不过其实没有太大必要，自己在自定义结构元中定义也一样可以用，且更加方便。

StrElem strel(int r, int type)
{
	StrElem se;
	switch(type)
	{
	case 1: // diamond
		se.len = (r*2 + 1)*(r*2 + 1);
		se.x = (int*)malloc(se.len*sizeof(int));
		se.y = (int*)malloc(se.len*sizeof(int));
		int idx = 0;
		for (int i = -r; i <= r; i++){
			for (int j = -r; j <= r; j++){
				if (abs(i) + abs(j) <= r){
					se.x[idx] = i;
					se.y[idx] = j;
					idx++;
				}
			}
		}
		break;
	case 2: // square
		se.len = 2*r*(r + 1) + 1;
		se.x = (int*)malloc(se.len*sizeof(int));
		se.y = (int*)malloc(se.len*sizeof(int));
		int idx = 0;
		for (int i = -r; i <= r; i++){
			for (int j = -r; j <= r; j++){
				se.x[idx] = i;
				se.y[idx] = j;
				idx++;
			}
		}
		break;
	}
	return se;
}

这里只定义了两种，分别是‘diamond’和‘square’

调用方式

StrElem se1 = strel(2, 1);//半径为2的钻石型核
StrElem se2 = strel(3, 2);//半径为3的正方形核

调用结果

腐蚀

腐蚀相对简单，因为不用考虑图像边缘的问题。

// 输出：图像  输入：原始图像，行，列，结构元半径，结构元类型
double** imerode2(double** in, int Rows, int Cols, int r, int type){
	// 初始化
	double** out = NULL;
	out = (double**)malloc(Rows * sizeof(double *));
	for (int i = 0; i < Rows; i++)
		out[i] = (double*)malloc(Cols * sizeof(double));
	for (int i = 0; i < Rows; i++)
		for (int j = 0; j < Cols; j++)
			out[i][j] = 0;
	// 腐蚀
	StrElem se;
	se = strel(r, type);
	for (int i = r; i < Rows-r; i++){	
		for (int j = r; j < Cols-r; j++){
			for (int k = 0; k < se.len; k++){
				if (in[i + se.x[k]][j + se.y[k]] < 1)
					goto p; // 判断是否整个结构元在目标内
			}
			out[i][j] = 1;
		p:;
		}
	}
	return out;
}

调用方式

double** im1 = imerode2(im, 512, 512, 10, 1);

调用结果

膨胀

膨胀的时候，目标可能会超出原图边界，所以要扩充原图

double** imdilate2(double** in, int Rows, int Cols, int r, int type){
	// 扩展图初始化
	double** tmpin = NULL, **tmpout = NULL;
	int tmpR = Rows + 2*r, tmpC = Cols + 2*r;
	tmpin = (double**)malloc(tmpR * sizeof(double *));
	tmpout = (double**)malloc(tmpR * sizeof(double *));
	for (int i = 0; i < tmpR; i++){
		tmpin [i] = (double*)malloc(tmpC * sizeof(double));
		tmpout [i] = (double*)malloc(tmpC * sizeof(double));
	}
	for (int i = 0; i < tmpR; i++)
		for (int j = 0; j < tmpC ; j++){
			tmpin [i][j] = 0;
			tmpout [i][j] = 0;
		}
	for (int i = 0; i < Rows; i++)
		for (int j = 0; j < Cols; j++)
			tmpin [i+r][j+r] = in[i][j];
	// 输出初始化
	double** out = NULL;
	out = (double**)malloc(Rows * sizeof(double *));
	for (int i = 0; i < Rows; i++)
		out[i] = (double*)malloc(Cols * sizeof(double));
	for (int i = 0; i < Rows; i++)
		for (int j = 0; j < Cols; j++)
			out[i][j] = 0;
	// 膨胀
	StrElem se;
	se = strel(r, type);
	for (int i = r; i < tmpR- r; i++)
		for (int j = r; j < tmpC - r; j++)
			if (tmpin[i][j]>0)
				for (int k = 0; k < se.len; k++)
					tmpout[i + se.x[k]][j + se.y[k]] = 1;
	// 截取赋值(保持与原图同尺寸)
	for (int i = 0; i < Rows; i++)
		for (int j = 0; j < Cols; j++)
			out[i][j] = tmpout [i+r][j+r];

    // free(别忘了释放)
    for (int i = 0; i < tmpR; i++){
        free(tmpin[i]);
        free(tmpout[i]);
    }
    free(tmpin);
    free(tmpout);
    
	return out;
}

调用方式

double** im2 = imdilate2(im, 512, 512, 10, 1);

调用结果

开闭运算

开运算

开运算 = 腐蚀+膨胀

// 开运算函数
double** imopen2(double** in, int Rows, int Cols, int r, int type) {
    // 先膨胀后腐蚀
    double** dilated = imdilate2(in, Rows, Cols, r, type);
    double** opened = imerode2(dilated, Rows, Cols, r, type);
    
    // 释放内存
    for (int i = 0; i < Rows; i++) {
        free(dilated[i]);
    }
    free(dilated);
    
    return opened;
}

闭运算

闭运算 = 膨胀+腐蚀

// 闭运算函数
double** imclose2(double** in, int Rows, int Cols, int r, int type) {
    // 先腐蚀后膨胀
    double** eroded = imerode2(in, Rows, Cols, r, type);
    double** closed = imdilate2(eroded, Rows, Cols, r, type);
    
    // 释放内存
    for (int i = 0; i < Rows; i++) {
        free(eroded[i]);
    }
    free(eroded);
    
    return closed;
}

调用示例

double** im3 = imopen2(im, 512, 512, 10, 1);
double** im4 = imclose2(im, 512, 512, 10, 1);

其中，im是输入的原始图像，512和512是图像的行数和列数，10是结构元半径，1是结构元类型。函数返回的im3和im4分别是进行开运算和闭运算后的图像结果。

引用文献及改动

算法原理

• 引用自腐蚀与膨胀算法。
  加入个人理解，删改段落，更改版式。

代码实现

• 引用自C语言二值图的腐蚀膨胀及开闭运算。
  在博主的代码基础上进一步编写了开运算和闭运算函数。