你的轻量化设计能有效提高模型的推理速度吗？

写在前面：本博客仅作记录学习之用，部分图片来自网络，如需引用请注明出处，同时如有侵犯您的权益，请联系删除！

---

---

前言

轻量化网络是指在保持较高性能的同时大大减少模型参数和计算量的神经网络模型。轻量化网络的出现是为了解决在移动设备和嵌入式系统等资源受限的环境中部署深度学习模型时所面临的挑战。

传统的深度学习模型通常包含大量的参数和复杂的计算结构，这使得它们在移动设备上运行时需要消耗大量的内存和计算资源。而轻量化网络通过精心设计结构和参数，可以在移动端实现更加高效的部署，从而适应移动设备上的应用需求。

因此轻量化网络的研究和发展是深度学习领域的一个重要方向，涉及网络结构设计、模型压缩、量化技术、剪枝等多个方面。通过对轻量化网络的研究，可以更好地适应各种应用场景的需求，推动深度学习技术向更广泛的领域拓展与应用。

相信不少小伙伴肯定经历过类似的情况，轻量化网络，参数减少极多，推理速度甚至不升反降。或者明明用了一些轻量化的网络结构，速度提升并不多，因此不妨反问自己以下问题：

• 利用深度可分离卷积，模型参数减少，浮点运算减少，推理速度真的也能提升吗？
• 利用多分支结构/并行结构降低了模型参数，真的能提高推理速度吗？
• 利用逐点卷积降低通道进而降低了模型参数和运算，真的能提高推理速度吗？
• 利用一些即插即用的轻量化网络设计就能有效提高推理速度吗？

答案是否定的。那如何才能有效的轻量化提高推理速度呢？影响网络推理速度的因素是什么？这些都会在本文中有所解释。

---

预备知识

模型的推理速度不仅和模型相关，也与内存的访存量相关，因此下文对其进行说明。

模型指标

Parameters： 表示模型参数数量以衡量模型大小，如卷积层中卷积核中参数与偏置参数。

FLOPS： "Floating Point Operations Per Second"的缩写，意为每秒浮点运算次数，通常衡量硬件性能。

FLOPs： "Floating Point Operations"的缩写，意为浮点运算数，通常衡量模型的计算复杂度。
常见的FLOPS的进制如下:

• 1 MFLOPS = $10^6$ FLOPS（megaFLOPS），等于每秒$10^6$次的浮点运算。
• 1 GFLOPS = $10^3$ MFLOPS（gigaFLOPS），等于每秒$10^9$次的浮点运算。
• 1 TFLOPS = $10^3$ GFLOPS（teraFLOPS），等于每秒$10^{12}$次的浮点运算。
• 1 PFLOPS = $10^3$ TFLOPS（petaFLOPS），等于每秒$10^{15}$次的浮点运算。
• 1 EFLOPS = $10^3$ PFLOPS（exaFLOPS），等于每秒$10^{18}$次的浮点运算。
• 1 ZFLOPS = $10^3$ EFLOPS（zettaFLOPS），等于每秒$10^{21}$的浮点运算。

Characterization and Benchmarking of Deep Learning

---

MACs： "Multiply–Accumulate Operations"的缩写，即乘加累积操作数，1MACs包含一个乘法操作与一个加法操作。

MACs和MAdds描述的是相同的内容。MAC 是 “Multiply–accumulate” 的缩写，MAdd 是 “Multiply-Add” 的缩写，都描述了乘法和加法结合的指令或运算，不同的处理器架构可能使用不同的术语，但它们都指向相同的概念。

一般来说，MACs与FLOPs存在一个2倍的关系，$2\times FLOPs=MACs$，因此在衡量网络时候，$tatle=m\times FLOPs=n\times MACs$，其中$m=2n$。在CNN中，卷积核与特征图的计算中加法计算次数总比乘法次数少一，。举个例子，对于卷积核K（大小为$n\times n$）和特征F之间的一次计算：$out={\sum }_{i=1}^{n^2}{F}_{loca{l}_i}\times K_i$，乘法次数 $n^2$，加法计算次数 $n^2-1$，也常将其近似为$n^{2}MACs$ 。因为在多数硬件中的乘加运算与乘法、加法运算具有相同的指令周期以提高计算效率，如现代处理器中的 SIMD（Single Instruction, Multiple Data）指令集通常会包含乘加指令，以支持并行的数据处理操作。

• ARM Cortex-A系列处理器：支持多种乘加指令，如VMLA（Vector Multiply Accumulate）和VFMA（Vector Fused Multiply Accumulate）等指令，用于执行SIMD操作，在单个时钟周期内完成多个数据元素的乘加运算。
• Intel x86系列处理器：支持多种乘加指令，如FMA（Fused Multiply-Add）指令和AVX2指令集中的VFMADD指令，在单个时钟周期内完成多个浮点数的乘加运算，从而提高计算效率。
• Nvidia GPU：Nvidia的GPU架构中支持多种乘加指令，如MAD（Multiply and Add）指令和FMA指令，可以在单个时钟周期内执行多个浮点数的乘加运算，并且支持并行计算，可以加速高性能计算和图形处理等任务。

MAC： “Memory Access Cost” 的缩写，即内存使用量，用来评价模型在运行时的内存占用情况。

MACs计算

卷积MACs

---

对于卷积核大小为K的传统卷积而言，$MACs=B\times K\times K\times C_{in}\times H_{out}\times W_{out}\times C_{out}$，B是Batch-size，实际MAC需要根据填充和步长确认输出特征的大小。

深度可分离卷积是将传统卷积分解为分组卷积和逐点卷积，占用的内存要少得多，速度更快。深度可分离卷积的 MACs 总数为分组卷积 + 逐点卷积，默认输出特征尺度不变：
$$MACs=K\times K\times C_{in}\times H_{out}\times W_{out}+1\times 1\times C_{in}\times H_{out}\times W_{out}\times C_{out}=C_{in}\times H_{out}\times W_{out}\times (K\times K+C_{out})$$

对于倒残差的结构，给定通道扩增因子$Facto{r}_{exp}$：
$$MACs=C_{in}\times H_{in}\times W_{in}\times C_{exp}+K\times K\times C_{exp}\times H_{out}\times W_{out}+C_{exp}\times H_{out}\times W_{out}\times C_{out}$$
$$=C_{in}\times H_{in}\times W_{in}\times C_{exp}+(K\times K+C_{out})\times C_{exp}\times H_{out}\times W_{out}$$
其中$C_{exp}=C_{in}\times Facto{r}_{exp}$， $Facto{r}_{exp}=2$ 时，与传统卷积的MACs相近。

全连接MACs

在全连接层中，所有输入都连接到所有输出。对于具有输入值为 $I$ 和输出值$J$ 的全连接，其权重可以存储在 $I\times J$ 矩阵中。全连接层执行的计算为：$y=matmul(x,W)+b$，其中 $x$ 是输入值的向量，$W$是包含层权重的 $I\times J$ 矩阵，$b$是偏差值。

为了计算 MACs 的数量，查看点积发生的位置，因此 MACs 的总数为 $I\times J$ ，与整个批次的权重矩阵的大小相同，此处批次大小为1。偏差不影响 MACs 的数量，在点积中的加法比乘法少一个，偏差值 $b$ 只会被吸收到最终的乘法累加中。

注意：全连接层的公式是在没有显式偏置值的情况下编写的。在这种情况下，偏差向量作为一行添加到权重矩阵中以使其成为 $(I+1)\times J$ ，会增加额外的乘法，MACs的数量都不会受到太大影响，此时MACs仅仅是一个近似值。意味着，全连接需要$I\times J$ MACs 或者 $(2I-1)\times J$ FLOPS。

激活函数MACs

激活函数
通常，卷积后面跟着一个非线性激活函数，例如 ReLU 或 Sigmoid，激活函数需要时间，但一般使用 FLOPs 来衡量，因为其不是点积，即乘加运算。
ReLU ：$y=max(x,0)$，是 GPU 上的单个操作，同时激活函数仅应用于输出，在具有J个输出神经元的全连接层上，ReLU 使用这些计算，将其计算为为 J FLOPs。

Sigmoid 激活的成本更高：$y=1/(1+exp(-x))$。在计算 FLOPs时，通常将加法、减法、乘法、除法、幂、平方根等算作一个 FLOP。由于Sigmoid 函数中有四个不同的操作，因此这将计为每个输出 4 个 FLOPs，或者总层输出的J × 4 FLOPS。这就是MobileNets发展与总结提到为什么使用h-swish代替swish的原因，实际上，忽略激活函数的计算代价是很常见的，因为它们只占用总时间的一小部分，绝大多数情况下不会成为计算瓶颈。

---

BN MACs

在现代网络中，通常在每个卷积层之后包含一个 BN 层。批量归一化将以下公式应用于每个输出值：$z=\gamma \ast (y-mean)/sqrt(variance+ϵ)+\beta$；其中y是上一层输出特征图中的一个元素，首先通过减去该输出通道的 并除以标准差来规范化此值，$ϵ$用于确保分母不为0，然后按$\gamma$进行缩放并添加偏差$\beta$。

每个通道都有的 gamma, beta, mean，variance ，因此如果卷积层有C个输出通道，则批量归一化层有C×4个可学习的参数。通常，BN应用于卷积层的输出，但在非线性 ReLU 之前，可以一些数学运算，使批处理范数层消失！如下：

换句话说，可以将BN的学习参数“折叠”到前一个卷积/全连接层的权重中。在上面的公式中，表示来自上一层的单个输出值y，进一步的：

$$z=\gamma \ast ((x[0]\ast w[0]+x[1]\ast w[1]+...+x[n-1]\ast w[n-1]+b)-mean)/sqrt(variance+ϵ)+\beta$$

其中，$x$表示输入数据，$w$是该层的权重，$b$是该层的偏差值。

为了将BN参数折叠到前一层中，重写这个方程，以便gamma, beta, mean, and variance仅适用于w和b但其中没有x，改写后：

$$w_{new}[i]=w[i]\ast \gamma /sqrt(variance+ϵ)$$
$$b_{new}=(b-mean)\ast \gamma /sqrt(variance+ϵ)+\beta$$
其中$w_{new}[i]$是第 i 个权重的新值，$b_{new}$是偏差的新值。

将这些值用于卷积层或全连接层的权重，得到：
$$z=x[0]\ast w_{new}[0]+x[1]\ast w_{new}[1]+...+x[n-1]\ast w_{new}[n-1]+b_{new}$$

一般来说，紧跟 BN的网络层本身通常没有偏差b，因为 BN层已经提供了一个 $\beta$公式$b_{new}$ 变得更简单一些（设置 $\beta =0$）：
$$b_{new}=\beta -mean\ast \gamma /sqrt(variance+ϵ)$$

因此，即使原始层没有偏差，它也会通过折叠的批量范数层获得偏差。总而言之，可以忽略BN的计算量影响。注意：上述只适用于顺序为：卷积、BN、ReLU 时才有效，甚至很多深度学习框架通常已经进行了优化集成。

---

存储访问

存储构成

系统存储：

• L1/L2/L3：多级缓存，其位置一般在CPU芯片内部；
• System DRAM：片外内存，内存条；
• Disk/Buffer：外部存储，如磁盘或者固态硬盘。

GPU设备存储：

• L1/L2 cache：多级缓存，其位置在GPU芯片内部；
• GPU DRAM：通常所指的显存；

传输通道：

• PCIE BUS：PCIE标准的数据通道，数据就是通过该通道从显卡到达主机；
• BUS： 总线。计算机内部各个存储之间交互数据的通道；
• PCIE-to-PCIE：显卡之间通过PCIE直接传输数据；
• NVLINK：显卡之间的一种专用的数据传输通道

内存访问量

内存访问量 ：通常涉及到两个主要方面：内存中数据的大小和访问模式。以下是一些常见的计算方式：

• 数据大小： 首先需要确定要访问的数据的大小，可以是单个变量、数组、结构体或其他数据结构，常以字节为单位进行计量。
• 访问模式： 内存访问模式包括顺序访问、随机访问、连续访问等。不同的访问模式可能会对内存访问量产生不同的影响。

• 顺序访问：数据按照地址的顺序被访问，每次访问将会取得相邻的数据，可以最大限度地利用 CPU 缓存，减少内存访问量。
• 随机访问：数据的访问是随机的，可能会导致更多的缓存未命中，增加内存访问量。

一般来说，内存访问量可以通过以下公式进行估算：
$$\text{内存访问量}=\text{数据大小}\times \text{访问次数}$$

对于GPU来说，内存访问量的计算方式与CPU有些不同。GPU的内部存储系统通常包括全局内存、共享内存和局部内存、L1/L2Cacha、寄存器（register）等。在GPU中，计算密集型任务通常会涉及大规模数据的并行处理，因此内存访问成为性能的一个关键因素。以下是一些与GPU内存访问量相关的因素：

全局内存访问： 全局内存是GPU中最大容量的内存，用于存储数据和指令，能被设备内的所有线程访问、全局共享。与CPU相比，GPU的全局内存访问速度较慢，因为运算单元不能直接的使用全局内存的数据，需要经过缓存。因此通过减少访问次数和访问的数据量来降低全局内存的访问量可以提高性能。

共享内存访问： 共享内存是GPU中每个线程块（Thread Block）共享的高速缓存，可以用于加速数据共享和通信。与全局内存相比，共享内存的访问速度更快。因此，在设计GPU程序时，可以尝试将频繁访问的数据放入共享内存中，以减少全局内存的访问量。

局部内存访问： 局部内存是每个线程私有的内存空间，在需要时可以用来存储临时数据，主要是用来解决当寄存器不足时的场景，即在线程申请的变量超过可用的寄存器大小的空间。与全局内存和共享内存相比，局部内存的访问速度较慢。因此，在GPU程序中，应尽量避免频繁地访问局部内存。

寄存器访问：线程能独立访问的资源，它所在的位置与局部内存不一样，是在片上（on chip）的存储，用来存储一些线程的暂存数据。寄存器的速度是访问中最快的，但是它的容量较小。

L1/L2缓存访问：L1/L2缓存的访问方式通常是由硬件自动管理的，其主要目的是尽可能地减少对主内存的访问。当GPU需要访问存储在主内存中的数据时，它首先会检查L1/L2缓存中是否存在该数据。如果存在，则可以直接从缓存中读取，而无需访问主内存。如果不存在，则必须从主内存中加载数据，并将其存储在L1/L2缓存中以供后续使用。

在GPU编程中，优化内存访问量是非常重要的，特别是对于大规模并行计算任务。减少内存访问量可以提高程序性能和效率。为了减少GPU内存访问量，可以考虑以下几个方面：

内存访问模式： 尽可能地利用局部性原理，例如空间局部性和时间局部性，以减少不必要的内存访问。优化内存访问模式可以减少数据传输和提高数据重用率。

数据布局： 合理安排数据的存储方式，使得数据在访问时可以保持连续性或者最小化跨界访问，从而减少内存访问量。

内存层次结构： 充分利用GPU内存的层次结构，尽可能使用快速访问的内存，如共享内存，以减少对全局内存的访问。

避免内存闪烁： 在GPU编程中，内存闪烁指的是频繁地在全局内存和其他内存之间进行数据传输，这会增加内存访问量和延迟。尽量减少内存闪烁可以降低内存访问量。

总之，优化GPU内存访问量需要综合考虑数据访问模式、数据布局、内存层次结构等因素，并根据具体的应用场景和硬件特性进行相应的优化策略。

---

轻量化结构

MobileNets

可移步MobileNets发展与总结，此处不过多赘述。总言之，使用分组卷积和逐点卷积替代传统的卷积，降低了网络的参数和FLOPs。

ShuffleNet

ShuffleNet V1

ShuffleNet V1： ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices
论文速递： 点击转跳

构建更深更大的卷积神经网络是解决主要视觉识别任务的主要趋势。最精确的CNN通常有数百层和数千个通道，因此需要数十亿FLOPs的计算。在非常有限的计算预算中，以数十或数百MFLOPs追求最佳精度是不切实际的，如无人机、机器人和智能手机等常见移动平台。

MobileNet利用深度可分离卷积，ShuffleNet以一种新的形式推广了分组卷积和深度可分卷积，对于给定的计算复杂度预算，允许更多的特征映射通道，有助于编码更多的信息，对非常小的网络的性能尤其重要，如下图，需要注意的是比常规的残差少一个Relu。

叠加分组卷积会导致来自某个通道的输出仅来自一小部分输入通道，如图(a)。如果允许分组卷积从不同的群体中获取输入数据，则输入和输出通道将完全相关。具体来说，对于前一层组层生成的特征映射，先将每一组中的通道划分为几个子组，然后为下一层的每一组提供不同的子组。

进而通过通道洗牌操作(图c)实现：假设一个卷积层具有g个组，其输出具有$g\times n$个通道；首先将输出通道维度重塑为$(g,n)$，转置然后将其平坦化，作为下一层的输入，信道洗牌是可微的，可进行端到端训练。

Xception和ResNeXt等在构建块中引入了高效的深度可分离卷积或分组卷积，从而在表示能力和计算成本之间取得了很好的平衡。在此进行对比，给定输入大小 $c\times h\times w$和瓶颈通道$m$，$g$是分组数：

• ResNet的MACs = $1\times 1\times c\times h\times w\times m+3\times 3\times m\times h\times w\times m+1\times 1\times m\times h\times w\times c=hw(2cm+9m^2)$
• ResNeXt的MACs = $1\times 1\times c\times h\times w\times m+3\times 3\times m/g\times h\times w\times m+1\times 1\times m\times h\times w\times c=hw(2cm+9m^2/g)$
• ShuffleNet的MACs =$1\times 1\times c/g\times h\times w\times m+3\times 3\times m/m\times h\times w\times m+1\times 1\times m/g\times h\times w\times c=hw(2cm/g+9m)$

尽管深度卷积通常具有非常低的理论复杂度，但很难在低功耗的移动设备上有效地实现，这可能是由于与其他密集操作相比，计算/内存访问比更差。在ShuffleNet单元中，只在瓶颈上使用深度卷积，以尽可能地避免开销，因此只是简单的使用深度可分离卷积只能降低网络参数（MobileNets发展与总结中有对其参数的计算），实际的推理速度并不一定提高。

ShuffleNet V1 - 代码实现

import torch
import torch.nn as nn
import torch.nn.functional as F

class ShuffleV1Block(nn.Module):
    def __init__(self, inp, oup, *, group, first_group, mid_channels, ksize, stride):
        super(ShuffleV1Block, self).__init__()
        self.stride = stride
        assert stride in [1, 2]

        self.mid_channels = mid_channels
        self.ksize = ksize
        pad = ksize // 2
        self.pad = pad
        self.inp = inp
        self.group = group

        if stride == 2:
            outputs = oup - inp
        else:
            outputs = oup

        branch_main_1 = [
            # pw
            nn.Conv2d(inp, mid_channels, 1, 1, 0, groups=1 if first_group else group, bias=False),
            nn.BatchNorm2d(mid_channels),
            nn.ReLU(inplace=True),
            # dw
            nn.Conv2d(mid_channels, mid_channels, ksize, stride, pad, groups=mid_channels, bias=False),
            nn.BatchNorm2d(mid_channels),
        ]
        branch_main_2 = [
            # pw-linear
            nn.Conv2d(mid_channels, outputs, 1, 1, 0, groups=group, bias=False),
            nn.BatchNorm2d(outputs),
        ]
        self.branch_main_1 = nn.Sequential(*branch_main_1)
        self.branch_main_2 = nn.Sequential(*branch_main_2)

        if stride == 2:
            self.branch_proj = nn.AvgPool2d(kernel_size=3, stride=2, padding=1)

    def forward(self, old_x):
        x = old_x
        x_proj = old_x
        x = self.branch_main_1(x)
        if self.group > 1:
            x = self.channel_shuffle(x)
        x = self.branch_main_2(x)
        if self.stride == 1:
            return F.relu(x + x_proj)
        elif self.stride == 2:
            return torch.cat((self.branch_proj(x_proj), F.relu(x)), 1)

    def channel_shuffle(self, x):
        batchsize, num_channels, height, width = x.data.size()
        assert num_channels % self.group == 0
        group_channels = num_channels // self.group
        
        x = x.reshape(batchsize, group_channels, self.group, height, width)
        x = x.permute(0, 2, 1, 3, 4)
        x = x.reshape(batchsize, num_channels, height, width)

        return x

代码来源

---

ShuffleNet V2

ShuffleNet V2： ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design
论文速递： 点击转跳

除了精度之外，计算复杂度是另一个重要的考虑因素。现实世界的任务通常旨在在目标平台(如硬件)和应用场景(如自动驾驶需要低延迟)给定的有限计算预算下获得最佳精度，激发了一系列朝着轻量化架构设计和更好的速度-精度权衡的工作，包括Xception， MobileNet， MobileNet V2， ShuffleNet，分组卷积和深度卷积在其中应用广泛。

间接指标(FLOPs)和直接指标(速度)度量之间的差异可归因于两个主要原因。首先，FLOPs没有考虑对速度有很大影响的几个重要因素。其中一个因素是内存访问成本(MAC)，在某些操作(如分组卷积)中，该成本占运行时的很大一部分，如下图。另一个是因素并行度，在相同的FLOPs下，具有高并行度的模型可能比具有低并行度的模型快得多。

其次，根据平台的不同，具有相同FLOPs的操作可能有不同的运行时间。如，早期的作品广泛使用张量分解来加速矩阵乘法，但是最新的CUDNN库专门针对3 × 3卷积进行了优化，导致张量分解在GPU上甚至更慢，当然也不能天真不能认为3 × 3卷积比1 × 1卷积慢9倍。

综上两点，有效的网络架构设计应该考虑如下两个原则：

• 使用直接指标来衡量网络(如推理速度)，而不是间接度量(如FLOPs或参数量)。
• 在目标平台上进行评估，因为不同的硬件设备的优化可能存在较大差异。

---

ShuffleNet V2设计灵感来源于ShuffleNet，故称为ShuffleNet V2，主要基于下列四个设计点：

相同的通道宽度最小化内存访问成本(MAC)： 现代网络通常采用深度可分离卷积，其中逐点卷积(即1 × 1卷积)占据了大部分复杂度，其中主要由两个参数指定：输入通道数$c_1$和输出通道数$c_2$，设h和w为特征图的宽高，则1 × 1卷积的FLOPs为 $B=h\times w\times c_1\times c_2$ 。

不妨假设计算设备中的缓存足够大，可以存储整个特征映射和参数。因此，内存访问成本(MAC)，或者内存访问操作的次数，是$MAC=h\times w\times (c_1+c_2)+c_1\times c_2$。

• 读取输入特征映射的内存访问次数：$h\times w\times (c_1+c_2)$
• 读取参数矩阵的内存访问次数：$c_1\times c_2$

$$MAC\ge 2hw\sqrt{c_1{c}_2}+c_1{c}_2=2\sqrt{hwB}+\frac{B}{hw}$$

• 因为 $a+b\ge 2\sqrt{ab}$，在$a=b$取得等号，因而上述不等式在$c_1=c_2$取得等号

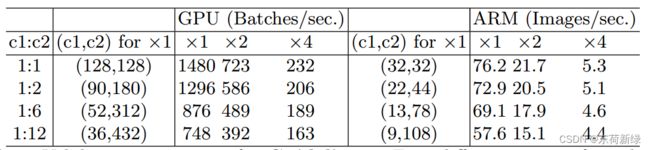
MAC有一个由FLOPs给出的下界，当且仅当输入和输出通道的数量相等时，它达到下界。结论是理论性的。实际上，许多设备上的缓存不够大。现代计算库通常采用复杂的阻塞策略来充分利用缓存机制。因此，实际MAC可能会偏离理论MAC。实验发现，如下表（单位时间的Batch越大速度越快），总FLOPs通过改变通道数来固定，当$c_1:c_2$趋近于1:1时，MAC越小，网络评估速度越快。

过多的分组卷积会增加MAC：
分组卷积是现代网络架构的核心，通过将所有信道之间的密集卷积变为稀疏(仅在信道组内)来降低计算复杂度(FLOPs)。一方面，它允许在给定固定FLOPs的情况下使用更多的通道，并增加网络容量(从而提高精度)。但是通道数量的增加导致MAC的增加。

形式上，1 × 1分组卷积的MAC和FLOPs之间的关系为
$$MAC=hw(c_1+c_2)+\frac{c_1{c}_2}{g}=hw{c}_1+\frac{Bg}{c_1}+\frac{B}{hw}$$

其中$g$为组数，$B=hw{c}_1{c}_2/g$ 为FLOPs。给定固定的输入形状 $c_1\times h\times w$ 和计算成本B, MAC随着 $g$ 的增长而增加，实验如下：

很明显，使用较大的组数会显著降低运行速度。在GPU上使用8组比使用1组(标准密集卷积)慢两倍多，在ARM上慢30%，这主要是由于MAC的增加。

因此，建议根据目标平台和任务，慎重选择分组数量，一味大的组数是不明智的，大组数带来的参数减小，FLOPs减小，准确性提高的优点很容易被增加的MAC成本所抵消，表现在推理速度不增反降。

网络碎片降低了并行度： 在GoogLeNet系列和自动生成的体系结构中，在每个网络块中广泛采用“多路径”结构。使用了许多小的操作符(“碎片操作符”)，而不是几个大的操作符。如，在NASNET-A中，碎片操作符的数量(即在一个构建块中单个卷积或池化操作的数量)为13，在像ResNet的规则结构中则是2或3。

碎片化结构已被证明有利于准确性，但它可能会降低效率，因为它对GPU等具有强大并行计算能力的设备不友好，此外还引入了额外的开销，如内核启动和同步，相信炼丹大师都有所体会，论文中的实验如下：

从上表结果可以看出，碎片化显著降低了GPU上的速度，如4-fragment结构比1-fragment结构慢3倍，在ARM上，速度降低相对较小。

元素操作不可忽略： 如下图，元素操作占用了相当多的时间，特别是在GPU上，包括ReLU、AddTensor、AddBias等。虽然具有较小的FLOPs，但相对较重的MAC。甚至说深度卷积也可看作类元素操作运算符，因为其具有较高的MAC/FLOPs比率，即具有小FLOPs，大MACs。

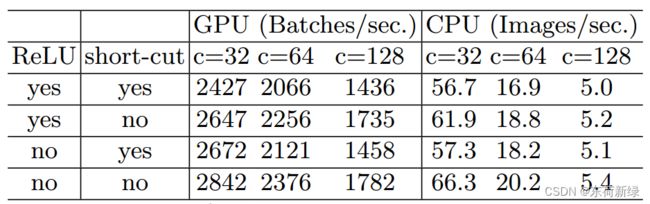
由上表，在移除ReLU和Short- Cut后，在GPU和ARM上都获得了大约20%的加速。

---

综上所述，一个高效的网络架构应该具备下列特点或设计网络在结合平台特性，如内存操作，代码优化的同时需要注意的点：

• 卷积具有相等的输入/输出通道
• 明确分组卷积的代价，避免过大的分组数目
• 降低网络碎片，不应具有大量的多路径结构
• 减少元素操作

进而设计ShuffleNet V2，为了获得较高的模型容量和效率，关键问题是如何在不密集卷积和不太多组的情况下保持大量等宽的通道，具体结构如下图：

在每个单元开始时，将c个特征通道的输入分为两个支路，分别为c - c0和c0通道。在G3之后，一个分支仍然是身份。另一个分支由三个具有相同输入和输出通道的卷积组成，以满足G1。其中两个1 × 1卷积不再是分组的，因为拆分操作已经产生了两个组。卷积后，两个分支通道堆叠起来。然后使“通道洗牌”操作来实现两个分支之间的信息通信。

总的来说，卷积全是等输入/输出通道，1 × 1卷积不再是分组的，通道拆分取代部分分组，通道洗牌来实现分支间的信息通信，并弃用add。

ShuffleNet v2不仅效率高，而且精度高。主要有两个原因。首先，每个构建块的效率高，可以使用更多的特征通道和更大的网络容量。

其次，在每个区块中，一半的特征通道(当c 0 = c/2时)直接穿过该区块并加入下一个区块。这可以看作是一种特征重用，与DenseNet和CondenseNet类似。

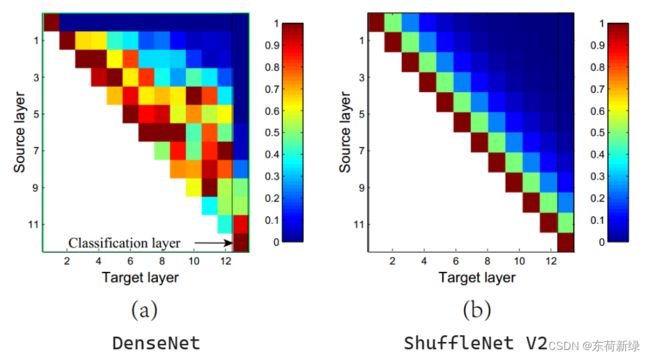
在DenseNet中，分析特征重用模式绘制了层间权值的11范数，如上图。很明显，相邻层之间的连接比其他层更强，意味着所有层之间的密集连接可能会引入冗余。ShuffleNet v2中特征重用的强度随着两个块之间的距离呈指数衰减，在相距较远的块之间，特性重用变得更弱，具有更少冗余。

ShuffleNet V2 - 代码实现

import torch
import torch.nn as nn

class ShuffleV2Block(nn.Module):
    def __init__(self, inp, oup, mid_channels, *, ksize, stride):
        super(ShuffleV2Block, self).__init__()
        self.stride = stride
        assert stride in [1, 2]

        self.mid_channels = mid_channels
        self.ksize = ksize
        pad = ksize // 2
        self.pad = pad
        self.inp = inp

        outputs = oup - inp

        branch_main = [
            # pw
            nn.Conv2d(inp, mid_channels, 1, 1, 0, bias=False),
            nn.BatchNorm2d(mid_channels),
            nn.ReLU(inplace=True),
            # dw
            nn.Conv2d(mid_channels, mid_channels, ksize, stride, pad, groups=mid_channels, bias=False),
            nn.BatchNorm2d(mid_channels),
            # pw-linear
            nn.Conv2d(mid_channels, outputs, 1, 1, 0, bias=False),
            nn.BatchNorm2d(outputs),
            nn.ReLU(inplace=True),
        ]
        self.branch_main = nn.Sequential(*branch_main)

        if stride == 2:
            branch_proj = [
                # dw
                nn.Conv2d(inp, inp, ksize, stride, pad, groups=inp, bias=False),
                nn.BatchNorm2d(inp),
                # pw-linear
                nn.Conv2d(inp, inp, 1, 1, 0, bias=False),
                nn.BatchNorm2d(inp),
                nn.ReLU(inplace=True),
            ]
            self.branch_proj = nn.Sequential(*branch_proj)
        else:
            self.branch_proj = None

    def forward(self, old_x):
        if self.stride==1:
            x_proj, x = self.channel_shuffle(old_x)
            return torch.cat((x_proj, self.branch_main(x)), 1)
        elif self.stride==2:
            x_proj = old_x
            x = old_x
            return torch.cat((self.branch_proj(x_proj), self.branch_main(x)), 1)

    def channel_shuffle(self, x):
        batchsize, num_channels, height, width = x.data.size()
        assert (num_channels % 4 == 0)
        x = x.reshape(batchsize * num_channels // 2, 2, height * width)
        x = x.permute(1, 0, 2)
        x = x.reshape(2, -1, num_channels // 2, height, width)
        return x[0], x[1]

---

GhostNets

GhostNet V1

GhostNet V1： GhostNet: More Features from Cheap Operations
论文速递： 点击转跳
开源代码： 点击转跳

传统的cnn通常需要大量的参数和浮点运算(FLOPs)才能达到令人满意的精度。因此，深度神经网络设计的最新趋势是探索具有可接受性能的移动设备的便携式和高效网络架构。

MobileNet利用深度卷积和点向卷积构建了基础单元，并取得了相当的性能。ShuffleNet进一步探索了一种通道洗牌操作增强轻量级模型的性能。

在训练良好的深度神经网络的特征图中，丰富甚至冗余的信息通常保证了对输入数据的全面理解。如下图给出了ResNet-50生成的输入图像的一些特征图，其中存在许多相似的特征图对，就像一个幽灵一样。

特征映射中的冗余是一个成功的深度神经网络的重要特征，而不是避免冗余的特征映射。
Ghost模块用更少的参数生成更多的特征。具体来说，深度神经网络中的普通卷积层将被分成两个部分。第一部分涉及普通卷积，但它们的总数将受到严格控制。即给定第一部分的固有特征映射，然后应用一系列简单的线性操作来生成更多的特征映射。

在不改变输出特征映射大小的情况下，与普通卷积神经网络相比，Ghost模块所需的参数数量和计算复杂度降低了，基于Ghost模块，建立了一个高效的神经网络架构，即GhostNet。

实验结果表明，提出的Ghost模块能够降低通用卷积层的计算成本，同时保持相似的识别性能，并且GhostNets可以在移动设备上快速推理的各种任务上超越最先进的高效深度模型，如MobileNetV3。

随着嵌入式设备对神经网络部署的需求，近年来提出了一系列紧凑模型。Xception利用深度卷积运算更有效地利用模型参数。MobileNets是一系列基于深度可分离卷积的轻量级深度神经网络。MobileNetV2提出了倒立剩余块，MobileNetV3进一步利用了AutoML技术，以更少的FLOPs实现了更好的性能。ShuffleNet引入了信道shuffle操作，以改善信道组之间的信息流交换。ShuffleNetV2在紧凑型模型设计中进一步考虑了目标硬件上的实际速度。

虽然这些模型以很少的FLOPs获得了很好的性能，但特征映射之间的相关性和冗余性从未得到很好的利用。

深度卷积神经网络通常由大量的卷积组成，带来了大量的计算成本。尽管最近的研究如MobileNet和ShuffleNet已经引入深度卷积或shuffle操作来使用较小的卷积滤波器(浮点数操作)构建高效的cnn，但剩余的1 × 1卷积层仍然会占用相当大的内存和FLOPs。

在实际中，给定输入数据 $X\in R^{c\times h\times w}$，其中c为输入通道数，h、w为输入的高度和宽度，任意卷积层产生n个特征映射的操作可以表示为：
$$Y=X\ast f+b$$
式中，∗为卷积运算，b为偏置项，$Y\in R^{h\times w\times n}$为有n个通道的输出特征映射，$f\in R^{c\times k\times k\times n}$为该层的卷积滤波器。其中，$h^{\prime }$和$w^{\prime }$分别为输出数据的高度和宽度，k × k分别为卷积滤波器f的核大小。在这个卷积过程中，所需的FLOPs数可以计算为$$n\cdot h^{\prime }\cdot w^{\prime }\cdot c\cdot k\cdot k$$，由于滤波器数n和通道数c通常非常大(例如256或512)，因此FLOPs数通常高达数十万。

卷积层的输出特征映射通常包含大量冗余，其中一些特征映射可能彼此相似。没有必要用大量的flop和参数逐个生成冗余的特征映射。假设输出的特征映射是一些具有廉价转换的内在特征映射的“幽灵”。这些内在特征映射通常较小，由普通卷积滤波器产生。具体来说，m个内在特征映射$Y^{\prime }\in R^{h^{\prime }\times w^{\prime }\times m}$是使用一次卷积生成的：$$Y^{\prime }=X\ast f^{\prime }$$

其中$f^{\prime }\in R^{c\times k\times k\times m}$为所使用的滤波器，$m\le n$，为简单起见，省略偏置项。

为了进一步获得期望的 $n$个特征映射，对 $Y^{\prime }$ 中的每个固有特征进行一系列廉价的线性操作，根据以下函数生成$s$个ghost特征:
$$y_{ij}={\Phi }_{i,j}(y_i^{\prime }),Vi=1,\cdots ,m,j=1,\cdots ,s$$

${\Phi }_{i,j}$是生成第j个ghost特征图$y_{ij}$ 的第 $j$ 次(最后一次除外)线性操作。在实践中，Ghost模块中可能有几种不同的线性操作，如3×3和5×5线性核。

复杂性分析： 利用Ghost模块来生成与普通卷积层相同数量的特征映射，因此可以轻松地将Ghost模块集成到现有设计良好的神经架构中，以降低计算成本，下面对内存使用和理论加速方面的收益进行说明。

不妨假设，有1个特征映射，m·(s−1)= n/s·(s−1)个线性操作，每个线性操作的平均核大小等于$d\times d$。理想情况下，n·(s−1)个线性操作可以有不同的形状和参数，考虑到在线推理CPU或GPU卡的效用，在一个Ghost模块中采用相同大小的线性操作(例如3 × 3或5 × 5)以实现高效推理。用Ghost模块升级普通卷积的理论加速比为：

其中d × d的大小与k × k的大小相似，s<

压缩比等于Ghost模块的加速比

Ghost瓶颈结构。利用Ghost模块的优势，引入了专为小型CNN设计的Ghost瓶颈(G-bneck)。如下图所示，Ghost瓶颈看起来类似于ResNet中的基本残差块，其中集成了几个卷积层和快捷方式，主要由两个堆叠的Ghost模块组成。

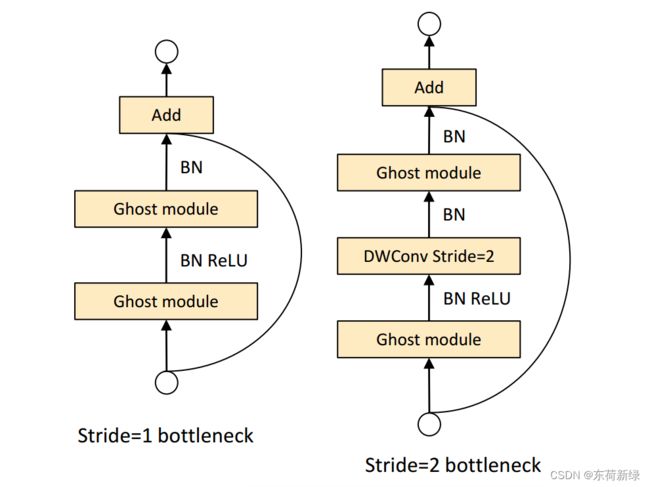
第一个Ghost模块作为扩展层增加通道的数量，将输出通道数与输入通道数之比称为扩展比。第二个Ghost模块减少了通道的数量以匹配残差。然后在这两个Ghost模块的输入和输出之间连接快捷方式。BN和ReLU非线性在每一层之后应用，参考MobileNetV2建议，在第二个Ghost模块之后不使用ReLU。

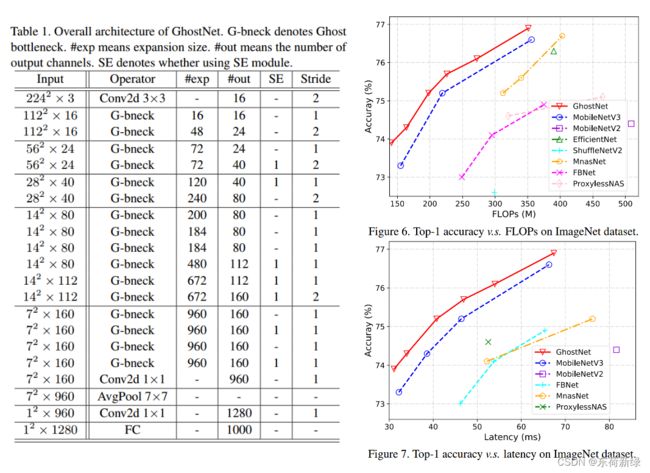
基于Ghost瓶颈，下表所示的所示的GhostNet。用Ghost瓶颈取代了MobileNetV3中的瓶颈块。GhostNet主要由Ghost模块作为构建块的Ghost瓶颈堆栈组成。第一层是具有16个滤波器的标准卷积层，然后是一系列信道逐渐增加的Ghost瓶颈。根据输入特征映射的大小，Ghost瓶颈被分成不同的阶段。除了每个阶段的最后一个瓶颈是stride=2之外，所有Ghost瓶颈都是在stride=1时应用的。

最后利用全局平均池化和卷积层将特征映射变换为1280维特征向量进行最终分类。SE模块也应用于某些虚瓶颈的残余层，最后实现轻量和性能的平衡。

为了降低现有深度神经网络的计算成本，Ghost模块将原始卷积层分成两部分，并使用较少的过滤器来生成几个内在特征映射。进一步应用一定数量的廉价转换操作来高效地生成Ghost特征图，是一种将原始模型转换为紧凑模型的即插即用模块，同时保持了可比较的性能。

GhostNet V1 - 代码实现

class GhostModule(nn.Module):
    def __init__(self, inp, oup, kernel_size=1, ratio=2, dw_size=3, stride=1, relu=True):
        super(GhostModule, self).__init__()
        self.oup = oup
        init_channels = math.ceil(oup / ratio)
        new_channels = init_channels*(ratio-1)

        self.primary_conv = nn.Sequential(
            nn.Conv2d(inp, init_channels, kernel_size, stride, kernel_size//2, bias=False),
            nn.BatchNorm2d(init_channels),
            nn.ReLU(inplace=True) if relu else nn.Sequential(),
        )

        self.cheap_operation = nn.Sequential(
            nn.Conv2d(init_channels, new_channels, dw_size, 1, dw_size//2, groups=init_channels, bias=False),
            nn.BatchNorm2d(new_channels),
            nn.ReLU(inplace=True) if relu else nn.Sequential(),
        )

    def forward(self, x):
        x1 = self.primary_conv(x)
        x2 = self.cheap_operation(x1)
        out = torch.cat([x1,x2], dim=1)
        return out[:,:self.oup,:,:]


class GhostBottleneck(nn.Module):
    """ Ghost bottleneck w/ optional SE"""

    def __init__(self, in_chs, mid_chs, out_chs, dw_kernel_size=3,
                 stride=1, act_layer=nn.ReLU, se_ratio=0.):
        super(GhostBottleneck, self).__init__()
        has_se = se_ratio is not None and se_ratio > 0.
        self.stride = stride

        # Point-wise expansion
        self.ghost1 = GhostModule(in_chs, mid_chs, relu=True)

        # Depth-wise convolution
        if self.stride > 1:
            self.conv_dw = nn.Conv2d(mid_chs, mid_chs, dw_kernel_size, stride=stride,
                             padding=(dw_kernel_size-1)//2,
                             groups=mid_chs, bias=False)
            self.bn_dw = nn.BatchNorm2d(mid_chs)

        # Squeeze-and-excitation
        if has_se:
            self.se = SqueezeExcite(mid_chs, se_ratio=se_ratio)
        else:
            self.se = None

        # Point-wise linear projection
        self.ghost2 = GhostModule(mid_chs, out_chs, relu=False)
        
        # shortcut
        if (in_chs == out_chs and self.stride == 1):
            self.shortcut = nn.Sequential()
        else:
            self.shortcut = nn.Sequential(
                nn.Conv2d(in_chs, in_chs, dw_kernel_size, stride=stride,
                       padding=(dw_kernel_size-1)//2, groups=in_chs, bias=False),
                nn.BatchNorm2d(in_chs),
                nn.Conv2d(in_chs, out_chs, 1, stride=1, padding=0, bias=False),
                nn.BatchNorm2d(out_chs),
            )


    def forward(self, x):
        residual = x

        # 1st ghost bottleneck
        x = self.ghost1(x)

        # Depth-wise convolution
        if self.stride > 1:
            x = self.conv_dw(x)
            x = self.bn_dw(x)

        # Squeeze-and-excitation
        if self.se is not None:
            x = self.se(x)

        # 2nd ghost bottleneck
        x = self.ghost2(x)
        
        x += self.shortcut(residual)
        return x

总结

模型的推理速度不仅和模型相关，也与内存的访存量相关。深度卷积通常具有非常低的理论复杂度，但很难在低功耗的移动设备上有效地实现，因为其计算/内存访问比较差。

总之，一个高效的网络架构应该具备下列特点或设计网络在结合平台特性，如内存操作，代码优化的同时需要注意的点：

• 卷积尽可能具有相等的输入/输出通道
• 分组卷积不易过大的分组数目
• 不应具有大量的多路径结构
• 减少元素操作

有时候使用简单线性操作来生成更多的特征映射也是不错的办法。最后减少通道和输入尺寸也是有效的提速的措施。

致谢

欲尽善本文，因所视短浅，怎奈所书皆是瞽言蒭议。行文至此，诚向予助与余者致以谢意。

---

参考

• CNN的参数量、计算量（FLOPs、MACs）与运行速度
• How fast is my model?
• GPU内存(显存)的理解与基本使用
• Zhang X, Zhou X, Lin M, et al. Shufflenet: An extremely efficient convolutional neural network for mobile devices[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2018: 6848-6856.
• Ma N, Zhang X, Zheng H T, et al. Shufflenet v2: Practical guidelines for efficient cnn architecture design[C]//Proceedings of the European conference on computer vision (ECCV). 2018: 116-131.
• Han K, Wang Y, Tian Q, et al. Ghostnet: More features from cheap operations[C]//Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2020: 1580-1589.