Java中浮点数精度误差产生原因_浮点数底层存储结构(详细附代码)
文章目录
-
- 概要
- 问题
- 原理 - 浮点数表示
- 原理小结
- 浮点数解析代码
- 代码解析,精度误差分析
- 结论
概要
本文为作者在学习阿里的《码处高效》时,对Java(JDK1.8)中浮点数底层的存储结构探究。由于float和double同理,但double位数过长,所以本文主要以float类型阐述。原理主要参考《码出高效》的浮点数章节,如果觉得枯燥乏味可以直接跳到代码解析部分。
代码解释主要以 16.35f 和 0.35f 中小数部分的存储值不同为例。
问题
懵逼的浮点数判断结果
System.out.println(0.1f + 0.2f == 0.3f); //输出true
System.out.println(0.1 + 0.2 == 0.3); //输出false
System.out.println(0.3f + 0.6f == 0.9f); //输出false
System.out.println(0.3 + 0.6 == 0.9); //输出false
提示:在此类问题中,编码时需要注意float基本数据类型需要添加后缀f,以及它的包装类Float的后缀F,不写后缀会默认为double类型。
一开始看到这个结果是不是直接懵了,先且不说不写后缀默认double的问题,第1和第3一个true一个false就直接懵逼了。
本文以《码出高效》中浮点数部分结合示例代码进行详细的解析,最终以16.35f和0.35f的存储值来说明为什么会出现以上结果。因为用double的话位数太多,容易看乱,相信大家通过float的解析可以触类旁通,所以本文就不再反复赘述了。
原理 - 浮点数表示
浮点数表示就是如何用二进制数表示符号、指数和有效数字。当前业界流行的浮点数标准是IEEE754, 该标准规定了 浮点数类型单精度、双精度、延伸单精度、延伸双精度。前两种类型是最常用的,它们的取值范围如下表所示:
| 精度 | 字节数 | 正数取值范围 | 负数取值范围 |
|---|---|---|---|
| 单精度类型 | 4 | 1.4e-45至3.4e+38 | -3.4e+38至-1.4e-45 |
| 双精度类型 | 8 | 4.9e-324至1.798e+308 | -1.798e+308至-4.9e-324 |
因为浮点数无法表示零值,所以取值范围分为两个区间:正数区间和负数区间。
以单精度类型float为例,它被分配了4个字节,总共 32 位,具体格式如下图所示:

指数称为“阶码”,有效数字称为“尾数”,所以用于存储符号、阶码、尾数的二进制位分别称为符号位、阶码位、尾数位,下面详细阐述三个部分的编码格式。
- 符号位
在最高二进制位上分配 位表示浮点数的符号,0表示正数,1表示负数 - 阶码位
在符号位右侧分配位用来存储指数,IEEE754标准规定阶码位存储的是指数对应的移码,而不是指数的原码或补码。根据计算机组成原理中对移码的定义可知,移码是将一个真值在数轴正向平移个偏移量之后得到的,即[x]移=x+2(n-1)(n为的二进制位数,含符号位)。移码的几何意义是把真值映射到个正数域,其特点是可以直观地反映两个真值的大小,即移码大的真值也大。基于这个特点,对计算机来说用移码比较两个真值的大小非常简单,只要高位对齐后逐个比较即可,不用考虑负号的问题,这也是阶码会采用移码表示的原因所在。
由于阶码实际存储的是指数的移码,所以指数与阶码之间的换算关系就是指数与它的移码之间的换算关系。假设指数的真值为e,阶码为E,则有E=e+(2(n-1)-1)其2(n-1)是IEEE754标准规定的偏移量,n=8是阶码的二进制位数。
为什么偏移值为2(n-1)-1而不是2(n-1)呢?因为8个二进制位能表示指数的取值范围为[-128,127],现在将指数变成移码表示,即将区间[128,127]正向平移到正数域,区间里的每个数都需要加上128,从而得到阶码范围为[0,255]。由于计算机规定阶码全为0或全为1两种情况被当作特殊值处理(全0被认为是机器零,全1被认为是无穷大),去除这两个特殊值,阶码的取值范围变成了[1,254]。如果偏移量不变仍为128的话,则根据换算关系公式[x]阶+128得到指数的范围变成[-127,126],指数最大只能取到126,显然会缩小浮点数能表示的取值范围。所以IEEE754标准规定单精度的阶码偏移量为2(n-1)-1(即127),这样能表示的指数范围为[-126,127],指数最大值能取到127 - 尾数位
最右侧分配连续的23位用来存储有效数字,IEEE754标准规定尾数以原码表示。正指数和有效数字的最大值决定了32位存储空间能够表示浮点数的十进制最大值。指数最大值为2127≈1.7×1038,而有效数字部分最大值是二进制的1.11···1(小数点后23),是个无限接近于2的数字,所以得到最大的十进制数为2×1.7×1038,再加上最左1位的符号,最终得到32位浮点数最大值为3.4e+38。
为了方便阅读,从右向左每4位用短横线断开:
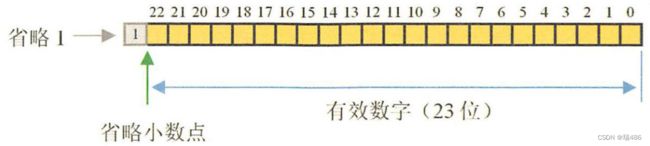
为了节约存储空间,将符合规格化尾数的首个1省略,所以尾数表面上是23位,却表示了24位二进制数,如下图所示:
常用浮点数的规格化表示如下表所示:
| 数值 | 浮点数二进制表示 | 说明 |
|---|---|---|
| -16 | 1100-0001-1000-0000-0000-0000-0000-0000 | 第1位为负数,131-127=4,即2的4次方等于16,尾数部分为1.0 |
| 16.35 | 0100-0001-1000-0010-1100-1100-1100-1101 | 符号位正,绿色部分上同,尾数部分见说明① |
| 0.35 | 0011-1110-1011-0011-0011-0011-0011-0011 | 此例的目的是说明16.35和0.35的尾数部分是不一样的 |
| 1.0 | 0011-1111-1000-0000-0000-0000-0000-0000 | 127-127=0即2的0次=1,尾数部分为1.0 |
| 0.9 | 0011-1111-0110-0110-0110-0110-0110-0110 | 126-127=-1即0.5② |
注意:
① 尾数部分的有效数字为1.00000101100110011001101,将其转换成十进制值为1.021875,然后乘以 24 得到16.35000038。由此可见,计算机实际存储的值可能与真值是不一样的。
② 0.9不能用有限二进制位精确表示,所以1-0.9并不精确地等于0.1,实际结果是0.100000024
原理小结
- float单精度浮点值的码偏移量为127
- 为了节约存储空间,将符合规格化(阶码偏移量大于等于0,其实就是大于等于1.0的浮点数)尾数的首个1省略,所以尾数表面上是23位,却表示了24位二进制数
对于float类型数据,其在计算机机器内部是二进制数,并用4个字节(32位)来表示。其中1位用于符号位,8位用于指数位,剩下的23位则用于存储“尾数”。此处的“尾数”是指数的底数,即223=8388608。因此,在Java中,float类型可以表示大约6-7位有效数字。最多能有7位有效数字,但能绝对保证的位数为6位。而double类型的浮点数采用64位存储结构。具体来说,这64位中包含:1位符号位,用于表示数值的正负;11位指数位,这部分采用偏正值表示,即实际的指数大小加上1023;剩下的52位是有效数位。这种设计使得double类型的数值范围可以达到-21024~ +21024(-1.79e+308 ~ +1.79e+308),并且有效位数可以达到16位。
需要注意的是,这里的有效数字位数指的是总位数,而不是小数点右边的数字。例如,float输出时,前7位有效数字是真实值,第8位是估算值,可能和原始一致,也可能是四舍五入上来的。
所以(反着写是因为这样小数位的比较更清晰)
0.10000000149011612 ≈ 0.1f
0.20000000298023224 ≈ 0.2f
0.30000001192092896 ≈ 0.3f
0.30000000447034836 ≈ 0.1f + 0.2f
float使用==比较的时候,截取6-7位,导致 System.out.println(0.1f + 0.2f == 0.3f); //输出true
若不写后缀,默认double,截取16位,导致System.out.println(0.1 + 0.2 == 0.3); //输出false
浮点数解析代码
import java.util.Arrays;
import java.util.concurrent.TimeUnit;
/**
* 浮点数底层研究
*
* @author LiaoYuXing-Ray
* @version 1.0
* @createDate 2024/1/4 10:01
**/
public class FloatAnalysis{
public static void main(String[] args) throws Exception {
// 需要计算真实存储值的浮点数
float floatValue1 = 16.35f;
float floatValue2 = .35f;
System.out.println(floatValue1 + "的真实存储值:" + rayFloatStudy(floatValue1));
System.out.println("\n========我是一条华丽的分割线========\n");
System.out.println(floatValue2 + "的真实存储值:" + rayFloatStudy(floatValue2));
}
/**
* 解析浮点数组成
*
* @param floatValue 待解析的浮点数
* @author LiaoYuXing-Ray 2024/1/4 10:01
**/
public static double rayFloatStudy(float floatValue) throws Exception {
// 符号位(1位)
byte[] symbol = new byte[1];
// 阶码位(8位),指数部分
byte[] exponent = new byte[8];
// 尾数位(23位),有效数字
byte[] number = new byte[23];
String binaryRepresentation = floatToBinary(floatValue);
System.out.println("浮点数\t" + floatValue);
System.out.println("========开始解析每一位的含义========");
System.out.println(binaryRepresentation);
byte[] byteString = binaryRepresentation.getBytes();
// float 4字节 1字节=8bit 所以32
byte[] byteArray = new byte[32];
// ASCII码中48是0 49是1
for (int i = 0; i < byteString.length; i++) {
if (byteString[i] == 48) {
byteArray[i] = 0;
} else if (byteString[i] == 49) {
byteArray[i] = 1;
} else {
throw new Exception("不应该出现的分支,理论上转为二进制只有0和1");
}
}
/*
以下是获取符号位、指数部分、有效数字的值,并输出
*/
for (int i = 0; i < byteArray.length; i++) {
if (i == 0) {
symbol[i] = byteArray[i];
}
if (i >= 1 && i <= 8) {
exponent[i - 1] = byteArray[i];
}
if (i > 8) {
number[i - 9] = byteArray[i];
}
// 以下为输出,可注释
if (i != 0 && i % 4 == 0) {
System.out.print("-");
}
System.out.print(byteArray[i]);
}
System.out.print("\n符号位值(1位):" + Arrays.toString(symbol));
if (symbol[0] == 0) {
System.out.print("为正数");
} else if (symbol[0] == 1) {
System.out.print("为负数");
} else {
throw new Exception("不应该出现的分支,符号位理论上只有0和1两种情况");
}
System.out.print("\n指数部分(8位):[");
for (byte b : exponent) {
System.out.print(b);
}
System.out.print("]\t-> 转化十进制数:[" + binaryToDecimal(exponent) + "]");
System.out.print("\n有效数字(23位):[");
for (byte b : number) {
System.out.print(b);
}
System.out.print("]");
System.out.println("\n=======还原float的真实存储值=======");
// 指数部分的十进制数值
int exponentOfDecimalNumber = binaryToDecimal(exponent);
/*
以 IEEE754 标准规定,单精度的阶码偏移量为 2^(n-1)-1 (即127),这样能表示的指数范围为 [-126,127]
*/
// 阶码偏移量
int offsetExponent = exponentOfDecimalNumber - 127;
System.out.println("阶码偏移量=指数部分的十进制数值[" + exponentOfDecimalNumber + "]- [2^(n-1)-1 (即127)]=" + offsetExponent);
// 指数值。此处double是因为Math.pow方法的参数为double类型
double integerBitsBaseValue;
if (offsetExponent >= 0) {
integerBitsBaseValue = 1 << offsetExponent;
} else {
integerBitsBaseValue = Math.pow(2D, offsetExponent);
}
System.out.println("指数值=2^阶码偏移量[" + offsetExponent + "]=" + integerBitsBaseValue);
// 整数部分(小数点左边的部分)即整数位(基础值)
double integerBits = integerBitsBaseValue;
// 有效位数转化为10进制数
double tempCount;
if (offsetExponent >= 0) {
tempCount = 1D;
// 如果偏移量大于等于0,整数部分为0
integerBits = 0;
System.out.println("整数部分(小数点左边的部分)即整数位(基础值)=" + integerBits);
System.out.println("尾数23位实际为1.xxx,尾数为有效数字加上1.0");
System.out.print("所以有效位数的二进制表示为[1.");
} else {
tempCount = 0D;
System.out.println("整数部分(小数点左边的部分)即整数位(基础值):" + integerBits);
System.out.println("尾数23位部分为0.xxx,尾数为有效数字加上0.0");
System.out.print("所以有效位数的二进制表示为[0.");
}
/*
此处计算小数二进制转化为十进制,比如0.01(2)=0*2^(-1)+1*2^(-2)=0.25(10)
*/
for (int i = 0; i < number.length; i++) {
if (number[i] == 1) {
// 将2的负(i+1)次方累加
tempCount += Math.pow(2, -(i + 1));
}
System.out.print(number[i]);
}
System.out.println("] -> 有效位数10进制数的值" + tempCount);
// 小数有效值
double decimalEffectiveValue = tempCount * integerBitsBaseValue;
System.out.println("(有效位数10进制数的值" + tempCount + ")*(指数值" + integerBitsBaseValue + ")=小数有效值:" + decimalEffectiveValue);
double result = decimalEffectiveValue + integerBits;
if (byteArray[0] == 0) {
System.err.println(floatValue + "为正数,小数有效值[" + decimalEffectiveValue + "]加上整数部分[" + integerBits + "],最终结果:" + result);
} else {
System.err.println(floatValue + "为负数结果需要*(-1),小数有效值[" + decimalEffectiveValue + "]加上整数部分[" + integerBits + "],最终结果:" + (result * -1));
}
// 休眠是因为防止err语句输出顺序混乱
try {
TimeUnit.MILLISECONDS.sleep(50);
} catch (InterruptedException e) {
e.printStackTrace();
}
return result;
}
/**
* 长度为8的byte[]转换为对应的十进制数
*
* @param exponentBytes 长度为8的byte[]
* @return int
* @author LiaoYuXing-Ray 2024/1/4 10:01
**/
private static int binaryToDecimal(byte[] exponentBytes) {
int decimal = 0;
for (int i = 0; i < exponentBytes.length; i++) {
decimal += (exponentBytes[i] & 0xFF) * Math.pow(2, exponentBytes.length - 1 - i);
}
return decimal;
}
/**
* 浮点型转化为bit,字符串输出,会自动补零
*
* @param value 浮点数
* @return java.lang.String
* @author LiaoYuXing-Ray 2024/1/4 10:01
**/
private static String floatToBinary(float value) {
int intBits = Float.floatToIntBits(value);
return String.format("%32s", Integer.toBinaryString(intBits)).replace(' ', '0');
}
}
代码解析,精度误差分析
下面我们通过运行结果分析浮点数精度误差产生的原因
首先通过Java内置的Float.floatToIntBits(value)方法将 16.35f 的底层二进制存储值进行还原:01000001100000101100110011001101
通过原理篇可知需要对其进行截取:符号位值(1位)、指数部分(8位)、有效数字(23位)
符号位值(1位):[0]为正数
指数部分(8位):[10000011] -> 转化十进制数:[131]
有效数字(23位):[00000101100110011001101]
由原理篇可知:
- 阶码偏移量 = 指数部分的十进制数值[131]-float的阶码偏移量 [2(n-1)-1] = 131-127 = 4
- 指数值 = 2阶码偏移量 = 24 = 16
- 整数部分(小数点左边的部分)即整数位(基础值) = 0.0 (因为阶码偏移量大于等于0)
- 尾数部分 = 1.021875023841858
由原理篇可知尾数23位的实际表示24位,因为阶码偏移量大于等于0,所以隐藏位为:1.xxx(反之隐藏位为0.xxx),所以尾数为有效数字加上1.0。所以有效位数的二进制 = 1.0 + 00000101100110011001101 = 1.00000101100110011001101。有效位数10进制数的值 = 1.021875023841858
关于小数二进制转十进制举例:1.01(二进制)= 1×20+0×2(-1)+1×2-2 = 1+0+0.25=1.25(十进制)
由于上面的值是代码逻辑计算出的,可以经过以下验算,验证尾数部分计算逻辑是正确的
double result0 = Math.pow(2, 0); // 1.0
double result1 = Math.pow(2, -6); // 0.015625
double result2 = Math.pow(2, -8); // 0.00390625
double result3 = Math.pow(2, -9); // 0.001953125
double result4 = Math.pow(2, -12); // 2.44140625E-4
double result5 = Math.pow(2, -13); // 1.220703125E-4
double result6 = Math.pow(2, -16); // 1.52587890625E-5
double result7 = Math.pow(2, -17); // 7.62939453125E-6
double result8 = Math.pow(2, -20); // 9.5367431640625E-7
double result9 = Math.pow(2, -21); // 4.76837158203125E-7
double result10 = Math.pow(2, -23); // 1.1920928955078125E-7
System.out.println(result0 + result1 + result2 + result3 + result4 + result5 + result6 + result7 + result8 + result9 + result10);
// 1.021875023841858
- 小数有效值 = (有效位数10进制数的值1.021875023841858)*(指数值16.0) = 16.350000381469727
- 最终得出真实存储值为 = 小数有效值[16.350000381469727]加上整数部分[0.0] = 16.350000381469727
通过System.out.printf("%.15f%n", 16.35f); // 输出: 16.350000381469727验证推导正确
如果是负数,结果需要*(-1)
需要区别的是:本节有效位数指的是float底层二进制存储位数
结论
所以针对文章开头的比较,现在可以验证,真实存储值保留6-7位有效数字的float,导致了巧合情况 0.1f +0.2f = 0.3f,而保留16位有效数字的double 0.1 + 0.2 ≠ 0.3
double f1 = FloatAnalysis.rayFloatStudy(0.1f);
double f2 = FloatAnalysis.rayFloatStudy(0.2f);
double f3 = FloatAnalysis.rayFloatStudy(0.3f);
double sum = f1 + f2;
System.out.println(f1 + "\t= 0.1f"); // 0.10000000149011612 = 0.1f
System.out.println(f2 + "\t= 0.2f"); // 0.20000000298023224 = 0.2f
System.out.println(f3 + "\t= 0.3f"); // 0.30000001192092896 = 0.3f
System.out.println(sum + "\t= 0.1f + 0.2f"); // 0.30000000447034836 = 0.1f + 0.2f
同理验证,无论取6-7位有效数字还是16位有效数字,0.3 + 0.6 均不会等于 0.9
double f3 = FloatAnalysis.rayFloatStudy(0.3f);
double f6 = FloatAnalysis.rayFloatStudy(0.6f);
double f9 = FloatAnalysis.rayFloatStudy(0.9f);
double sum = f3 + f6;
System.out.println(f3 + "\t= 0.3f"); // 0.30000001192092896 = 0.3f
System.out.println(f6 + "\t= 0.6f"); // 0.6000000238418579 = 0.6f
System.out.println(f9 + "\t= 0.9f"); // 0.8999999761581421 = 0.9f
System.out.println(sum + "\t= 0.3f + 0.6f"); // 0.9000000357627869 = 0.3f + 0.6f
由于浮点数的底层存储数据结构的原因,所以在比较浮点数的时候,通常建议不要使用 == 运算符来比较两个浮点数是否相等,而是使用一个小的容差值来进行比较,例如:
float
float num1 = 0.1f + 0.2f;
float num2 = 0.3f;
float epsilon = 1e-6f;
if (Math.abs(num1 - num2) < epsilon) {
System.out.println("相等");
} else {
System.out.println("不相等");
}
double
double a = 0.1d + 0.2d;
double b = 0.3d;
double epsilon = 1e-10d;
if (Math.abs(a - b) < epsilon) {
System.out.println("相等");
} else {
System.out.println("不相等");
}
在理解了原理之后,使用代码辅助验证会更清晰有助于理解,希望本文能够对您有所帮助。部分原理和图片使用《码出高效》,本文是作者对其的粗浅理解,可能存在一些错误或不完善之处,如有遗漏或错误欢迎各位补充。