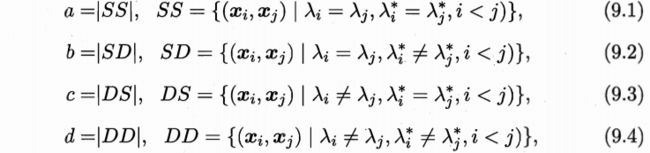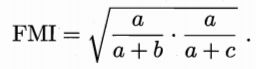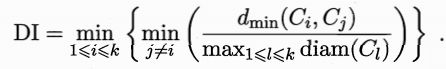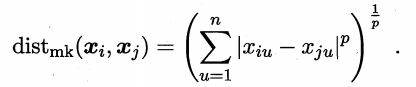第九章 聚类

9.1 聚类任务

 聚类是试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集称为一个“簇”。通过这样的划分，每个簇可能对应于一些潜在的概念（类别）。但是这些概念对聚类算法而言事先是未知的，聚类过程仅能自动形成簇结构，簇所对应的概念语义需要由使用者来把握和命名。

• 聚类算法涉及的两个基本的问题：性能度量和距离计算

9.2 性能度量

1. 聚类性能度量大致有两类。一类是将聚类结果与某个“参考模型”进行比较，称为“外部指标”；另一类是直接考察聚类结果而不是利用任何参考模型，称为“内部指标”

2. 基于以下式子常用的聚类性能度量外部指标：
   

• 对于数据$D$={$x1,x2,....,xm$},假定通过聚类给出的簇划分为C={$c1,c2,...,ck$},参考模型给出的簇划分为C^*={$c1$^*,$c2$^*,…,$cs$^*}.相应的，令$\lambda$,$\lambda$^*分别表示与C和C^*对应的簇标记向量。

• 集合SS包含了在C中隶属于相同簇且在C*中也属于相同簇的样本对

• 集合SD包含了在C中隶属于相同簇且在C*中隶属于不同簇的样本对，DS，DD同理

• 其中a+b+c+d=m(m-1)/2

• jaccard系数
  

• FM指数
  

• Randy指数
  
  上述性能度量值范围均在[0,1]区间内，值越大越好

4. 基于（9.8-9.11）可导出下面一些常用的聚类性能度量内部指标：
   
   其中，$dist(.,.)$用于计算两个样本之间的距离；$u$代表簇C的中心点,|C|代表C中样本点的个数。

• DB指数：
  
• Dunn指数：
  
  显然，DBI越小越好，DI则越大越好。

9.3 距离计算

1. “距离度量”满足的一些基本特性：
   （1）非负性：$dist$(x_i,x_j)>=0；
   （2）同一性：$dist$(x_i,x_j)=0当且仅当x_i=x_j；
   （3）对称性：$dist$(x_i,x_j)=dist(x_j,x_i)；
   （4）值递性：$dist$(x_i,x_j)<=dist(x_i,x_k)+dist(x_k,x_j).
2. 几种距离的计算方法
    给定样本x_i=(x_i1;x_i2;…;x_in)与x_j= (x_j1;x_j2;…x_jn)

• 闵可夫斯基距离
  
• 欧氏距离
   当p=2时，闵可夫斯基距离变为欧式距离
  
• 曼哈顿距离
   当p=1时，闵可夫斯基距离为曼哈顿距离
  
• 切比雪夫距离
  当p->∞时为切比雪夫距离

3. 有序属性和无序属性
   有序属性： 能直接在属性上计算距离，如定义域为{1，2，3}的离散属性，“1”与“2”比较接近、与“3”比较远，这样的属性称为有序属性。
   无序属性： 定义域为{飞机，火车，轮船}，这样的离散属性则不能直接在属性上计算距离，称为无序属性。

4. 无序属性的距离计算：VDM距离
   
    其中m_u,a表示在属性u上取值为a的样本数，m_u,a,i表示在第i个样本簇中在属性u上取值为a的样本数，k为样本簇数。

5. 混合属性的计算可利用闵可夫斯基距离和VDM结合
    假设有n_c个有序属性、n-n_c个无序属性，不失一般性，令有序属性排列在无序属性之前，将闵可夫斯基距离和VDM结合即可处理混合属性：
   
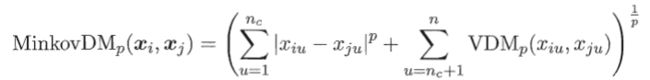
   当样本空间中不同属性的重要程度不同时，可以使用加权距离，下面为加权闵可夫斯基距离：
   
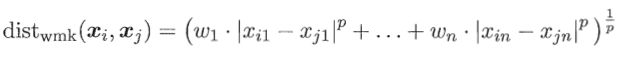
   其中，权重$w$ _i>=0(i=1,2,…n)表征不同属性的重要性，通常$w$_i之和等于1

9.4 原型聚类

9.4.1 k均值法（k-means）
  给定样本集D={$x1,x2.....,x$_m}针对聚类所得簇划分C={C₁,C₂,…,C_k}最小化平方差

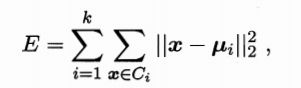
其中$u$_i是簇C_i的均值向量，即C_i中所有样本的均值
以下列数据集为例，K-means算法过程如下：

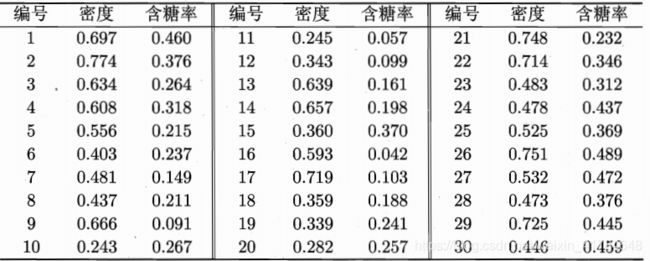
有数据集可知，聚类簇数k=3
 (1）随机从三个聚类簇中选取三个样本来作为初始向量值如$x6,x12,x27$

（2）计算数据集中每个样本点与$u$₁,$u$₂,$u$₃的距离，然后判别该样本点距离哪个簇的距离最近，即将该样本划分到这个簇中，如x1距离均值向量u₁,$u$₂,$u$₃的距离分别是0.369,0.506,0.166,因此将该点归入簇C₃中。经过第一遍考察后：

（3）从新划分的簇中求出新的均值向量

（4）重复步骤（2）（3）得到新的划分簇和均值向量，直到C₁，C₂,C₃不在变化
 
9.4.2 学习向量化（LVQ）
  与k均值算法类似，LVQ试图找到一组原型向量来刻画聚类结构，但与一般的聚类算法不同的是，LVQ假设的数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。
以上面的数据集为例，其中令9-21号样本标记为$c$₂,其他样本标记为c₁。假定q=5,即学习目标是找到5个原型向量$p1$,$p2$,$p3,p4,p5$,并假定其对应的类别标记分别为$c1,c2,c2,c1,c1$,对第q个簇可从类别标记为t_q的样本中随机选取一个作为原型向量，例如书中p₁的初始化向量为x₅,则是因为p1的类别分类标记是c1，初始化向量则是从c1的标记样本中随机抽取的，LVQ算法的实现过程如下：
（1）初始化原型向量及学习率
（2）计算每个样本与初始化向量之间的距离，将该样本标记该初始化向量的标记并利用公式p’=p+学习率·（x-p）来更新原型向量。
（3）重复更新过程，直到满足条件。
9.4.3 高斯混合聚类
 与k均值、LVQ用原型向量来刻画聚类结构不同，高斯混合聚类采用概率模型来表达聚类原型。
高斯混合聚类算法如下：

9.5 密度聚类

 

9.6 层次聚类

 

参考数据：机器学习《周志华》