深搜 排列数字

吉林大学毕业生 MythCoffee 东北师范大学附属中学OJ 2023.04.29

题目 排列数字

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入样例：

输入格式

共一行，包含一个整数 n。

输出格式

按字典序输出所有排列方案，每个方案占一行。

数据范围

1≤n≤8

输入样例：

3

输出样例：

1 2 3

1 3 2

2 1 3

2 3 1

3 1 2

3 2 1

---

分析过程

这是前天一个小型考试的一道普通的题目。但是这道题有很多可以讲的地方。

这道题总得来说，有几个疑问：

1. 怎么想到用深搜来解这道题的？
2. 它作为一道深搜题，本身却不具有任何“图”“树”属性，为什么？
3. 这道题除了深搜还有什么方法解决？

/* 金圣明老师插句话，欢迎各位留言告诉我你不会的题目哦，评论区就行ε=(´ο｀*)))都不知道大家需要什么题解*/

那今天咱们就解决这三个问题（摩拳擦掌）

第一个问题，怎么想到用深搜的？

我个人来讲呢，如果你是一个非竞赛生或者刚刚接触这部分内容，那么我推荐用一个分析方法来看该不该用深搜。（以下方法仅供参考）

1. 原理上（手动算）没有比一个一个试验更好的办法
2. 满足树理、图理的 「向下查找、遇错返回」
3. 可以用很多层的for循环实现
4. 深度或者遍历次数出现诸如26,2*10^5，n的n次方这些暗示

出现上面的一个或者多个，那么至少可以说明深搜是可用的。但具体能不能AC要再继续分析，后续我会写一写这部分内容。

那么这道题，满足可以用很多层for循环实现这个条件，也满足条件一……

不对！条件一不满足！

这时候就要展示出来我的做题经验了（叉腰骄傲 ），不知道各位有没有做过一道题，大概是叫做下一个排列，题目要求是让你求出任意一个排列的下一个排列。说着有点绕，我写一个

输入：
5
1 3 4 2 5

输出：
1 3 4 5 2

大概就是这样，输出下一个排列。

这道题是有简单解法的！不用逐层循环！所以这道题并不满足条件一，有比一个一个试验更好的办法。但具体能不能用我们一会上手一试，先来完成深搜部分。

由于是满足多个for循环这个高分条件的，因为很显然用N个for循环就能遍历所有可能，所以可以用深搜解决。

但是！怎么循环是个问题。

我们用最大的数据n=8来做这道题

最朴实（笨 ）的方法，我们需要从10000000（1千万）遍历到99999999（1亿-1），
我们需要做的大概是这样的：

for（i 从一千万到一亿减一）
{
	数位分离
	如果有数字被用了两次，则无效
}

我只能说，emmmm，有一种朴实的愚蠢 蕴含其中

那么我们把数位分离拆出来

for(i 从1到9)
{
	for(i2 从0到9)
	{
	…………
		for(i8 从0到9)
		{
			如果有数字被用了两次，则无效
		}
	}
}

省略了一大坨for循环嵌套。在这里其实已经有点深搜的感觉了。但是时间代价上还是有点超标，因为判断数字被用两次这个操作，耗费的时间其实也是一层循环。所以看起来不超，但实际上已经越线了。

于是把判断过程外移，并做一点显著的优化

for(i 从1到9)
{
如果当前数字被使用则跳过
	for(i2 从0到9)
	{
	如果当前数字被使用则跳过
	…………
		for(i8 从0到9)
		{
			如果当前数字被使用则跳过
		}
	}
}

到这里已经可以说是比较顺眼了，11******、22、33、……、99**这些被去掉了之后至少减少了1/10之一的无效查找。也就是解放了一层循环，时间上已经可以过了。但我们还能做得更好

h = 1+2+3+4+5+6+7+8 = 36
for(i 从1到9)
{
如果当前数字被使用则跳过
h = h - i
	for(i2 从0到9)
	{
	如果当前数字被使用则跳过
	h = h - i2
	…………
		for(i7 从0到9)
		{
			如果当前数字被使用则跳过
			h = h - i7
			剩下的h 就是 i8
		}
	}
}

这里有两个变化，一个是循环少了一层，另一个是用h去表示i8，解释一下为什么这么做。

以下两个性质叫做缺席法。

你班级里面有5个人（假设），你给他们命名，叫1 2 4 8 16

每天上课前，你要求孩子们把数字加在一起，那么拿到数字的时候，你就能通过二进制的方式，知道今天来了几个孩子，哪几个来了。

如 11010 = 26 当你拿到26这个数的时候，表示1（1号）和4（3号）没来
11110 = 30 拿到30表示1没来
这个就叫做1248码原理。

那么如果班级里每次只会缺少一个学生，那么还能简化一些。可以用12345678……来命名学生。1到n求和就是h，用h减去你拿到的数，就能得到谁没到位。

比如 36-30 = 6 表示8个人的班级，如果7个人都到位了，那么缺的一定是6号。

我把这两种方法命名为缺席法。对应上面的循环我们就知道了，当我们确定了n-1层的数字互相不重复的时候，其实最后一个数字只有一个能够选择了。而这个数字就是等差数列求和减去前面选择的数字。也就是循环少了一层的原因和用h计数器的原因。

当然，你愿意用二进制缺席法，那是更好的，就是打起来会稍微麻烦一点点，也不多 。

以上，我们已经完成了n=8的情况下所有力所能及的优化。之后，就是将循环改深搜了。

这一步我知道对初学者很难，但篇幅所限，以后我会仔细讲讲深搜的（请关注我！）。代码我扔在下面，需要请自取。

那么到这里，第一个问题“怎么想到用深搜来解这道题的？”和第二个问题“它作为一道深搜题，本身却不具有任何“图”“树”属性，为什么？”，解释的差不多了。

这俩问题其实都出自不知道什么时候用深搜。上面的那4个选项可以记录一下，大多数时候还是蛮不错的。

再解释下第二个问题，如果我们画一下方案树，就可以发现：

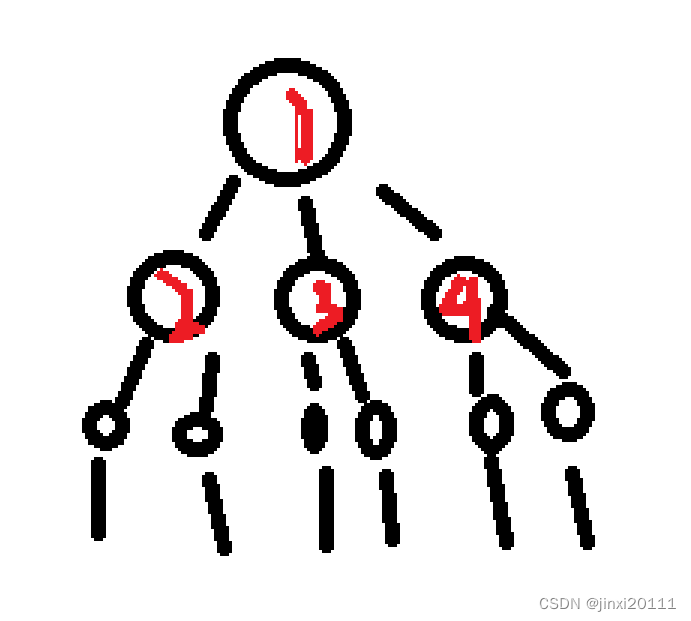
图丑了点，但应该能看懂，排列问题本身就是一个树状结构问题。所以用深搜合情合理。

我对深搜的理解：高级一点的暴力，本质还是暴力。

如果你看了这句话能悟到点什么，那证明你悟性很不错或者你已经有了自己的思考。如果没太看懂……

请关注我后，见下回分解（跑）

这回前两个问题解释完了，看看下个问题：

这道题除了深搜还有什么方法解决？

---

有一个生成下个排列的函数，叫做next_permutation好像是，我记得一个库里面是有这个函数的。但是这个东西不是啥难理解的东西，还是要学一下原理的。

我举个例子 2143这个东西找下一个排列大家肯定都会，是2314，但是具体怎么做的好像就是一想就出来了。

其实很简单。我们从右往左找相邻的顺序对
2 1 4 3 中，4 3 不是 1 4是，当我们找到一对的时候停住，
标记左侧位置x（1，位置为2），然后在该数的右侧，找到比它大的最小的数，标记其位置y（3，位置为4）

之后

1. 交换两个数的位置 2143 → 2341
2. 将x右侧全部数从小到大排序。2341→2314

这样就完成了一次next操作。

分析下时间，n个数的情况下，有n的阶乘个排列。8的阶乘有40320。然后循环中要进行一次从左到右和一次8个数的排序，大概是400万。应该是可以操作的。

目前来看，这个方法是可以一用的。代码量可预见的不大。

那么三个问题就都解决完毕了。

以下就是我在考试时候的AC代码了。next_permutation就留到以后再写或者去别人那看看吧！还是得给别的博主留口饭是吧 （就是懒了，苹果键盘真的好不舒服啊！！）

啊对，由于输出数据40320*8 加上空格，是超过了iostream的分水岭的，所以要换标准输入输出哦

以上！ 有问题可以加我的微信 MythLucky详聊哦！
// 吉林大学毕业生 东北师范大学附属中学OJ 2023.04.29

#include
#include
using namespace std;
int ans[10],n,h,x;
bool b[10];
void dfs(int deep)
{
	if (deep==n){
		x=h;
		for(int i=1;i<n;i++)
		{
			x-=ans[i];
			printf("%d ",ans[i]);
		}
		printf("%d\n",x);
		return;	
	}
	for(int i=1;i<=n;i++)
	{
		if (b[i]){
			ans[deep]=i;
			b[i]=false;
			dfs(deep+1);
			b[i]=true;
		}
	}
}
int main(){
	scanf("%d",&n);
	h=(1+n)*n/2;
	for(int i=1;i<=n;i++){
		b[i]=true;
	}
	dfs(1);
	return 0;
}