数位DP:我的理解与模板【java实现】
数位DP
前言
这个星期研究了好几天的数位DP问题,已经摸到一点门路了,所以写篇笔记记录一下,用于之后的复习。
我的做法完全参考自y总的思路和代码,只不过采用java实现,第二节的例题也是,第三节使用leetcode几道原题。
另外还参考了这位大佬的博客,大家也可以去看看,题目比我的更全。
y总的课性价比超高,以后有票了买一波课回去研究研究。这里只列了他讲的比较简单的几题,力扣的题目就更简单了(虽然标签都是hard…),若想深入研究可以去听课。
PS: 数位dp难度较高(基本上入门题在力扣都是hard),编码有些意识流的赶脚,找工作面试出现概率应该是非常低的,我只是出于兴趣研究的,如果赶时间可以不学。
一、问题描述和算法概述
特征:[l, r]区间中,满足某条件的数或者数字的数量。
由名知义:
- 数位:即算法的实现针对某个数的每个数位的数字进行讨论;
- dp:需要实现预处理一个dp数组帮助接下来的求解。
技巧:假设[1, r]区间符合条件的数为k,[1, l - 1]的结果为t,那么[l, r]的结果就是k - t【前缀和思想】
因此,下面专门来讨论[1, n]区间的问题。
一些我们约法三章的表示:
1)n:条件约束的上界,我们需要进行数位讨论的依据;[下面假设n=9143]
2)N:n的位数;【即4】《下面的算法实现中我都写作了len》
3)i:n当前讨论到的数位,数位大的i较大;【比如,讨论到十位,i=1,百位就是2】;
4)x:当前数位值【比如讨论到10位,即i=1时,x=4】
5)j:被x完全覆盖的区间中的某个数【比如讨论到10位,j∈[0, x - 1], 即[0, 3]】;
6)f:dp数组,即数位讨论之前预处理好的数组,用于直接计算被x或者n完全覆盖情况下的解;
本质:一个类似决策树的多次决策的过程,通过预处理的dp数组来对可以完全覆盖的部分区间进行直接求解,而单纯只对原数n的每个数位x进行深入讨论的算法。
ps:一定要额外上心
完全覆盖这四个字,它意味着可以直接求解,这是数位dp从始至终最重要的解题思想,也是算法高效性的体现。
图示:
根据上图,我们可以明显看到数位dp的几个特点:
1)除了start以外,每个原数n的数位(从大到小)作为父节点,他的左子树是一个范围,即比其右子树的数字的更小的所有数字,右子树为n下一个数位上的数字;
2)左子树深度永远为1【这是数位dp高效的根本原因:左子树表示范围中的所有数可以直接利用f求解,即左子树是可以确定被n完全覆盖的】;
难点:
1)预处理数组f的计算;【按照力扣的水平,大约是一个中等偏上,有时候能够达到hard难度的dp问题,但是它的状态表示往往较为固定,因此难度大约就是中等】;
2)数位讨论过程的处理【这里有很多的技巧,下面的题目也会尽量展示一些技巧。】
正好应和了数位dp这个名字,两个部分都是比较难的。
套路:
1)f的状态定义:f往往是两维,f[i][j]的i往往表示数的位数(包含前导0),j往往表示首位选择了什么数字[0~9];
为了能够准确表示数位的实际值,f[0][x]我们往往选择丢弃。
2)f的状态转移:往往也比较固定,大约是:
f [ i ] [ j ] = ∑ 0 → 9 f [ i − 1 ] [ k ] f[i][j] = \sum_{0 \to 9}{f[i-1][k]} f[i][j]=0→9∑f[i−1][k]
但是题目有时候会有别的条件,需要进行额外的处理;
3)数位讨论往往从高往低,即
i : N − 1 → 0 i: N - 1\to 0 i:N−1→0
4)前导0的处理:某些题目对于前导0有严格的要求,比如"求1000以内不含重复数字的数的个数",如果算上前导0,任何1位数都肯定不满足,因为1会被写作0001,就会存在3个0,不符合题意;但是实际上我们知道,个位数是肯定符合的,遇到这种情况,我们需要强制要求第一位,即i=N-1时,必须让j的范围为[1, x - 1], 即不考虑0
但是,只是这样做,我们会失去所有不足N位数的答案,为此,我们需要另外在数位讨论外额外讨论不足N位的所有解。
又因为不足N位数的数一定比n小,所以是被n完全覆盖的,因此可以利用f直接求解。
5)利用last记录之前的右节点的选择造成的某些限制;
6)最右节点特殊讨论【这个节点的出现表示n本身也是一个可行解,需要将结果加上一些值(因为不会再有左子树来直接求解了,会丢失累加这个可行解)】
ps:第一节看完,想必大多数人是不知所云的,请耐心看完第二节三道题,回头再看第一节,然后自己把这三题不看我的实现一遍,相信你一定会有所悟。
二、经典例题
这一节中,会给出三个较为典型的模板题,基本上都比力扣上的难一些,出自于y总的数位dp课程之上。
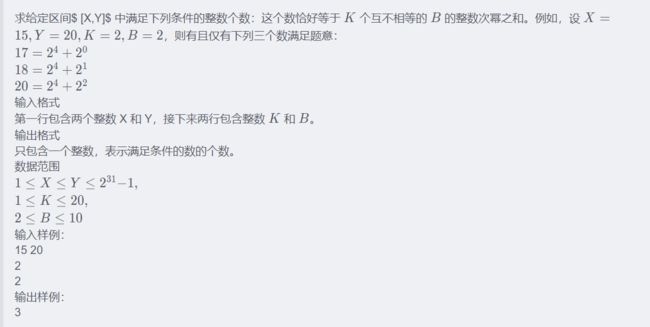
1. b进制数,恰好为若干个k个不同整数次幂之和
题目比较难以理解,来解释一下:
以10进制为例,若k=3,1101就是一个符合条件的4位数,而2111和1100就不是,前者是因为10^3(千位数)包含了系数2,在分解整数次幂时会变成10^3 + 10^3 + 10^2 + 10^1 + 10^0, 10^3出现了两次,不符合不同的整数次幂之和这个要求;后者是因为参与求和的10的整数次幂不足3个。
PS:这题是帮助理解
完全覆盖这种现象最好的题,可能有些难理解,自己需要画出几个符合条件的数的例子来帮助理解。
套路分析:
0)前导0考虑:这题是0和1的组合问题,无论如何都是N位数,即使不足N位都会补齐到N位,因此1实际就是0001这样,所以前导0无需考虑。
1)预处理f数组:
状态定义:f[i][j]: 位数为i的数(数字只能0/1)中,拥有j个1的数字个数
这个第一题状态定义就把我第一节的套路给反驳了。。。这其实与所求的目标有关,第一维是位数基本上是固定的,而我们必须要考虑到1的个数为k的限制,于是把1的个数这个状态放到第二维。
又因为我们的数字取值只可能是0或者1,所以只要我们考虑这j个1放到哪些数位上,就可以确定整个数字,又变成了i个位置选取j个位置放1的问题,显然,这是一个组合问题。
想必大家学过一个组合公式:
C n m = C n − 1 m − 1 + C n − 1 m C^m_n=C^{m-1}_{n-1}+C^m_{n-1} Cnm=Cn−1m−1+Cn−1m
实际含义很好理解:我们要在n个东西中选m个,不失一般性,考虑这n个东西的任何一个x,对于这个x,我们有不重不漏的两种情况:
- 选取x:那么接下来的问题就是从不包含x的n-1个中选取m-1个;
- 不选取x:子问题就是从不包含x的n-1个中选取m个。
可以得到f的状态转移也是这个形式。
PS: 这个组合公式本身就很有阎氏dp分析法的味道,选不选x就是最后一步,由此将所有组合方案划分两个子集合,来累计这两个子集合。
2)状态转移:不再赘述;
3)last定义:我们需要之前已经选取的1的数量来帮助确定接下来还需要的1的数量,即还需要k-last个1;
4)提前结束:我们要求每个b的整数幂次的系数必须要是0或者1,因此,只要任何一个x为大于1的数,就会提前结束;
5)最后一步:若能转移到i=0,说明起码第一个条件,即每个b的整数幂次的系数必须要是0或者1达到了,还差第二个条件,数字1的数量必须为k,若能达到,说明右边界也是一个有效解。
后面的题我只会分析到这里,但是这题比较难以理解,我再对较难的几个部分做下介绍,以帮助理解
完全覆盖,可以先看代码
class Solution1 {
/**
* 求[x, y]区间中,表示为b进制时,所含有的幂次的系数全部为1或者0的数的个数。
* 如,1011(十进制)= 1 * 10^3 + 0 * 10^2 + 1 * 10^1 + 1 * 10^0
* 实际上,求得是一类x,当将x表示为b进制时,和为x的所有b幂次的系数`全为1`
*/
public int solve(int x, int y, int k, int b) {
return dp(y, b, k) - dp(x - 1, b, k);
}
// f[i][j]:求i位b进制数中,数字只有0和1的情况下,1的个数为j的数的个数。
static final int N = 32;
static int[][] f = new int[N + 1][N + 1]; // 从数位最多为二进制考虑,即最大为32位,也就最多有32个1
static {
//习惯性的不考虑任何i=0的情况
for (int i = 1; i <= N; i++) {
// 从i位数中选取0个1,当前只有全为为0这种解了。
f[i][0] = 1;
}
f[1][1] = 1; //f[1][i] = 0, (i > 1)
for (int i = 2; i <= N; i++) {
for (int j = 1; j <= N; j++) {
// 求i位中1的个数位j的情况,就是求1的排列数
// 从动态规划角度考虑:i位数j个1,对于任何一个数位,只有两种情况:
// 1)为0,则就需要在剩下的i-1个数中得到j个1;
// 2)为1,就需要在剩下i-1个数中得到j-1个1.
f[i][j] = f[i - 1][j - 1] + f[i - 1][j];
}
}
}
// 将区间问题,统一转化为[0, n]的问题,这样区间问题就变成了dp(y) - dp(x - 1)问题。
public int dp(int n, int b, int k) {
if (n == 0) {
// 看题意,必须处理0防止bits为空。
return 1;
}
// 1. 获取数位
// 1)预估数位个数:32位整数位数最多的进制为2进制,即32位,剩下所有进制都没有32个,故开辟32位作为数位数组是足够的
int[] bits = new int[32];
// 2) 得到每个数位,高位在最后一位
int len = 0;
while (n != 0) {
bits[len++] = n % b;
n /= b;
}
// 2. 模板部分
int res = 0; // 结果变量,根据实际情况可能是一个数组
int last = 0; // 保存dp树右边界的上一个状态,这里记录有边界上已经取得的1的数量【这个设置初始值比较有讲究,需要满足不能干扰第一次遍历的特点,本题中,我们想要的是n表示为b进制时,1的数量,所以0不会干扰求解】。
for (int i = len - 1; i >= 0; i--) { // 习惯上都是从高位向着低位探索
int x = bits[i];
if (x >= 1) { // 若当前位为0,那么为了保证右边界的数能够小于等于原数【之前每一位全部都相等】,只能填0,因此这一位可以直接跳过,被固定死了
// 只要当前位大于0,那么结果集里面,当前位为0的全部答案都能被覆盖,这就让这个穷举的问题变成了一个可以直接求解的问题
// (PS:这个`通过结果集覆盖某个分支而直接求解这个分支`的思想是数位DP的核心,而`直接求解`这件事本身是数位DP另一个要点,就是上面的预处理数组f)
res += f[i + 1][k - last]; // 将当前位置固定为0后,后面无论怎么取都能满足`? < n`, 所以可以通过预处理直接求解[?指通过排列0,1得到的目标数]
if (x > 1) {
// 同理,若当前位置大于1,则可以取得当前数位为1的全部解【无论后面怎么排列,都必定满足? < n】,故可以直接求解
if (k - last - 1 >= 0) {
res += f[i + 1][k - last - 1]; // 可以取1的另一个条件是,右边界上全部的1的数量last仍然小于k
}
// 因为右子树的含义是:`?的第i位取当前数位值x的情况下`,接下来的情况数; 而这题要求的是只能取1或者0,而此时的x>1,不符合条件,右子树被直接剪枝
break;
} else {
// 由于当前位置刚好为1,解集合没能完全覆盖这个分支,所以只能继续`递归`求解
last++;
if (last > k) {
// 但是,若是右子树取了这个1以后,导致右边界1的数量已经超过了k,那么右子树下的任何解都必定不满足要求,直接剪枝
break;
}
}
}
if (i == 0 && last == k) {
// 右边界本身【即n本身】就是一个可行解,而我们即将退出循环,导致这个可行解没有考虑到,在这里补上
res++;
}
}
return res;
}
}
解释:
在数位讨论中,根据x的不同取值,有三种情况:
1)x=0,不可能存在被x完全覆盖的j,即
左子树是不存在的,因此无需考虑左子树,直接继续考虑右子树即可。举个例子,n=1103,我们已经考虑到了十位,那么就是要找一个符合11XY的数,我们可以将X选择位不为0的任何数吗?显然不行,不论X是大于0的任何数字,都绝对会大于n本身;
数位dp中,有两种情况是
绝对大于的:1)数位数量较大,这是一种数量级的碾压,数位数量大的绝对大;2)数位一样,前面i-1位也是一样,但是第i位时,第一个数大于另外一个,也是绝对大于的,上面就是情况2;
2)x=1:1能够完全覆盖的只有0,因此我们直接计算所有此位为0的解,表示就是`f[i + 1][k - last]`【有人可能会对取i+1有些不解,这是因为我们是从len-1遍历到0,i表示起始是数位数量少1,而我们f的定义是第一维就是数位的数量,因此这里求解i需要加一】;举个例子,n=1103,我们已经考虑到了百位,那么就是要找一个符合1XYZ的数。此时,只要X取0,那么任何形如10YZ的数都是小于n的数,而YZ本身就是一个二位数,又可以随意取0或者1【当然要满足1的数量要为k-last个】,这不就刚好满足我们f[2][k-last]的状态定义吗?
3)x>1: 首先,我们完全覆盖了0和1,针对0和1都能直接求解,0的求解和2)一样,1的求解当前需要将所需要的1的数量从k-last降低一个,即f[i + 1][k - last - 1];其次,我们获取了一个不符合条件的数位x, 因此这里需要终止循环举个例子,n=1133,我们已经考虑完了十位,那么下一步就去探索一个113x的右子树,但是,无论x取什么,113x都不会一个满足要求的解,因为中间十位的系数不是0或者1.
2. [x,y]中不降数的数量
不降数:十进制表示中,高位到低位每位数字单调递增【不能递减,如1124就是一个不降数】
套路分析:
0)前导0考虑:若一个不含前导0的数是不降数,那么在它前面无论加多少个0都是不降数。
1)取值范围:
10进制表示,int表示最多为20亿,即10位数;
数字个数依然是0~9,因此最大为10个;
2)状态定义:f[i][j]: i位数中,第一位数字为j的不降数个数
状态转移:
由阎氏dp分析法:最后一步是取决于第二位数字k的取值,由于满足不降的性质,k>=j ,因此F
f [ i ] [ j ] = ∑ 0 → 9 f [ i − 1 ] [ k ] , k < = j f[i][j] = \sum_{0 \to 9}{f[i-1][k]}, k <= j f[i][j]=0→9∑f[i−1][k],k<=j
3)last定义:我们要求不降的性质,last只需要记录上一位的取值即可;
4)提前结束条件:n的某些位数发生了逆序,即x 比如[11,12]中,数字1和2的累计个数为3和1,其他数字都是0 这题可能是三题中最难的一道。。。 特殊点: 由于是 套路分析: 0)前导0分析:由于可能就是要求0的数量,若包含前导0,显然不符合题意(实现n为5位数,那么难道每个个位数为都有4个0?显然很不对劲!) 不考虑前导0的话,就需要:1)数位讨论时,第一位不能取0;2)退出后,额外考虑所有不足N位的情况。 1)取值范围:位数:最多10位;数字0~9,共10位;当前处理的数字:共10位 2)状态定义: 3)状态转移: 阎氏dp分析法:k的数量只与我们选取的第二位(即i-1位)数字有关,主要分为两类: 4)last定义:我们需要之前所有的数字k的数量,这点和状态转移中情况2类似:左分支每多一种选择,之前所有的右边界上1都会重复10^i(i为当前左分支所在的数字位数) 以1132,当前求1的数量为例,在考虑十位数时,前面我们已经选择千位和百位上两个1,而十位数我们有02三种选择,且都是可以完全覆盖的(比如我们若选择0,110x都会被1132覆盖),而每个选择都会因为个位数的选择而重复10次,110x就会有11001109 10个数,同理选择1,2也是如此,即每个选择都累加10^1=10种; 5)退出条件:无需退出 6)最右节点:累计右边界上所有k即可。 到这里之前,我默认你已经复习了第一节并实现了上面三个算法。 我们可以给出数位dp的java模板: 有了模板以后,应该难度可以降低很多。下面就用力扣上的题目实操一下吧,希望你先去自己做(套模板)再来看我的做法,很有可能你的更好。 while (n > 0) {class Solution2 {
/**
* 求[x,y]中不降数的数量。
* 不降数:十进制表示中,高位到低位每位数字单调递增
*/
public int solve(int x, int y) {
return dp(y) - dp(x - 1);
}
// ~~有i位数,当首位为j的情况下的不降数个数~~
// static int[][] f = new int[11][10];//11:32位整数的最大值为20亿,即10位数,故位数取值范围为[0, 10];
// 10:十进制的取值可能只有10种。
static int[][] f = new int[11][10];
static {
// 由于删去了0状态,此时i表示有i+1位数。
Arrays.fill(f[1], 1);// 只有一位数,故取值只有一种
for (int i = 2; i <= 10; i++) {
for (int j = 0; j <= 9; j++) {
for (int k = j; k <= 9; k++) {
// f[i][j]的值是上一位取比j小的情况下所有的可能累加。
f[i][j] += f[i - 1][k];
}
}
}
}
private int dp(int n) {
if (n == 0) {
return 1;
}
// 1. 获取数位
int[] bits = new int[10];
int len = 0;
while (n != 0) {
bits[len++] = n % 10;
n /= 10;
}
// 2. 两个变量
int res = 0;
int last = 0; // 要想last不对第一位的取值产生任何影响,就需要`last<=第一位任何可以取的值`,0就可以了
// 3. 逐位分析
for (int i = len - 1; i >= 0; i--) {
int x = bits[i];
for (int k = last; k < x; k++) {// 只要当前位置取值比x更小,就能被解集全部覆盖【处于左子树下】,可以直接求解
// 当前位为第i位,即一共(i + 1)位,根据f的定义,f[i][j] 表示一共i+1位时且首位为j的解,故此时为f[i][k](共i+1位,首位为k)
res += f[i + 1][k];
}
if (last > x) {
break;
}
// 继续探索右子树
last = x;
// 若右边界的组合[原数]也是一个不降数,要在退出循环前加上
if (i == 0) {
res++;
}
}
return res;
}
}
3. [x, y]中所有十进制数中每位数字的累计个数
每位数字,显然我们根据每种数字分别处理,一共10次处理是最方便的,同样在状态定义中,为了对数字无差别统一处理,我们也需要额外的一维来记录当前处理的是哪个数字。f[i][j][k]:i位数中,最高位是j,满足这样性质的数中数字k的数量
f[i - 1][0][k]到f[i - 1][9][k]即可得到所有的低位解
class Solution3 {
//f[i][j][k]: 以j开头所有可能的i位数中,含有数字k的数目
static int[][][] f = new int[11][10][10];
static {
for (int i = 0; i < 10; i++) {
//一位数时,只有这个数字就是k,才会含有一个k
f[1][i][i] = 1;
}
for (int i = 2; i <= 10; i++) {
for (int j = 0; j < 10; j++) {
for (int k = 0; k < 10; k++) {
//计算i位数低位的k的数量
for (int x = 0; x < 10; x++) {
f[i][j][k] += f[i - 1][x][k];
}
//计算i位数中最高位k的数量
if (j == k) {
//当最高位就是k时,会增加k + 0~10^i-1这些排列,共10^i
//例如,查询1xx的数量(三位数),若最高位为1,那么就会多100~199共100种百位数为k的数字
f[i][j][k] += (int)Math.pow(10, i);
}
}
}
}
}
//计数问题:计算a~b之间,所有0~9各位数字出现的次数
public int[] solve(int x, int y) {
int[] res = new int[10];
for (int i = 0; i < 10; i++) {
res[i] = dp(y, i) - dp(x - 1, i);
}
return res;
}
private int dp(int n, int d) {
int[] bits = new int[10];
int len = 0;
while (n > 0) {
bits[len++] = n % 10;
n /= 10;
}
int res = 0;
//记录右边界上d的数量
int last = 0;
for (int i = len - 1; i >= 0; i--) {
int x = bits[i];
int s = i == len - 1 ? 1 : 0;
for (int j = s; j < x; j++) {
res += f[i + 1][j][d];
}
//TODO: 难点
//左分支每个选择都需要额外加上之前所有的d*10^(i+1)
res += last * (int)Math.pow(10, i + 1) * x;
if (x == d) {
last++;
}
if (i == 0) {
res += last;
}
}
//不足N位数
for (int i = 1; i < len; i++) {
//第一位必须是非0
for (int j = 1; j <= 9; j++) {
res += f[i][j][d];
}
}
return res;
}
}
三、小结
class Solution {
static int[][] f = new int[11][10];
static {
for (int j = 0; j <= 9; j++) {
//f[i][x]的定义
}
for (int i = 2; i <= 10; i++) {
for (int j = 0; j <= 9; j++) {
for (int k = 0; k <= 9; k++) {
//根据题意可能剔除某些k
//很多都会有下面这个等式
f[i][j] += f[i - 1][k];
}
}
}
}
int solve(int l, int r) {
return dp(r) - dp(l - 1);
}
int dp(int n) {
if (n == 0) {
return 1;
}
int[] bits = new int[10];
int len = 0;
while (n > 0) {
bits[len++] = n % 10;
n /= 10;
}
int res = 0;
//记录右边界上的状态
int last = 0;
for (int i = len - 1; i >= 0; i--) {
int x = bits[i];
for (int j = 0; j < x; j++) {
//大部分都有这个式子
res += f[i + 1][j];
}
if (x与last的关系不符合某个条件) {
break;
}
//根据last的定义进行更新
last = x;
//求解到最右节点,考虑右边界是否满足条件,满足则加一
if (i == 0) {
res++;
}
}
return res;
}
}
四、力扣上的数位DP
357
class Solution {
//f[i] : 9 * 8 * 7 ... (i个乘数)
//i-1位数可行的解的数量【我这里选择用0表示1位数...】
static int[] f = new int[10];
static {
f[0] = 1;
for (int i = 1; i <= 9; i++) {
f[i] = f[i - 1] * (10 - i);
}
}
public int countNumbersWithUniqueDigits(int n) {
if (n == 0) {
return 1;
}
//0算是一个可行解。
int res = 1;
//由于第一位必定是1,之后必定是0,1时只能进入右分支,而第一位不能为0,之后0没有左分支,相当于每一位都不能有变化,循环就没有必要了
//讨论不足n + 1位的情况
for (int i = 1; i <= n; i++) {
//不足n+1位,必定小于10^n, 就可以直接利用公式求解
res += 9 * f[i - 1];
//其实与下面这种经典写法等价。
/**
//首位必须大于0
for (int i = 1; i <= 9; i++) {
res += f[i - 1];
}
*/
}
return res;
}
}
600
class Solution {
public int findIntegers(int n) {
//这个直接当作dp函数
if (n == 0) {
return 1;
}
// 1. 获取数位
int[] bits = new int[32];
int j = 0;
while (n != 0) {
bits[j++] = n % 2;
n /= 2;
}
//2. 两个变量
int res = 0;
int last = 0; //右边界中,上个数是什么,取0的话,将对下个数位取值无影响
//3. 逐位考虑
for (int i = j - 1; i >= 0; i--) {
int x = bits[i];
if (x == 1) {//若x==0,当前固定死了只能取0,不会对结果产生影响, 直接跳过
//取1时,可以完整囊括左子树(取0)的所有解
res += f[i + 1][0];
if (last == 1) {
//右子树将不符合要求,没有深入探索的必要
break;
}
}
last = x;
if (i == 0) {
//右边界也是一个有效解
res++;
}
}
return res;
}
//i个二进制位中,最高位选择了j(0/1)时,含有的方案数
static int[][] f = new int[33][2];
static {
//只有一位,也只有一种选择
f[1][0] = 1;
f[1][1] = 1;
for (int i = 2; i <= 32; i++) {
f[i][0] = f[i - 1][0] + f[i - 1][1];
f[i][1] = f[i - 1][0];
}
}
}
902
class Solution {
public int atMostNGivenDigitSet(String[] digits, int n) {
int[] bits = new int[10];
int len = 0;
while (n != 0) {
bits[len++] = n % 10;
n /= 10;
}
int m = digits.length;
int[] nums = new int[m];
for (int i = 0; i < m; i++) {
nums[i] = Integer.parseInt(digits[i]);
}
int res = 0;
for (int i = len - 1; i >= 0; i--) {
int x = bits[i];
//二分查找第一个小于x的位置
int lo = 0, hi = m - 1;
while (lo < hi) {
int mid = (hi + lo + 1) >> 1;
if (nums[mid] >= x) {
hi = mid - 1;
} else {
lo = mid;
}
}
if (nums[lo] >= x) {
lo = -1;
}
res += (lo + 1) * pow(m, i);
//右分支被剪枝[右分支的这位数字不存在]
if (Arrays.binarySearch(nums, x) < 0) {
break;
}
if (i == 0) {
//n自身也是可行解。
res++;
}
}
//不足len位数的方案
for (int i = 1; i < len; i++) {
res += pow(m, i);
}
return res;
}
private int pow(int n, int t) {
return (int)Math.pow(n, t);
}
}
1012
class Solution {
//小于等于n且不存在重复数字的数个数
public int dp(int n) {
int[] bits = new int[10];
int len = 0;
while (n > 0) {
bits[len++] = n % 10;
n /= 10;
}
int res = 0;
//已经选了多少个数了
int last = 0;
//记录右边界选过哪些数
boolean[] v = new boolean[10];
for (int i = len - 1; i >= 0; i--) {
int x = bits[i];
if (i == len - 1) {
//第一位,只能在1~x-1中选
res += (x - 1) * count(i, 9);
} else {
//其他位都可以在0~x-1中选
//需要去掉之前选过的数字
int t = x;
for (int j = 0; j < x; j++) {
if (v[j]) {
t--;
}
}
res += t * count(i, 9 - last);
}
if (v[x]) {
break;
} else {
v[x] = true;
}
last++;
if (i == 0) {
res++;
}
}
//不足N位的答案
//都小于n,可以直接求得
for (int i = 1; i < len; i++) {
//第一位必须大于0
res += count(i - 1, 9) * 9;
}
return res;
}
//从s开始,一共n个数,即A(s, s - n + 1)
private int count(int n, int s) {
int res = 1;
for (int i = 0; i < n; i++) {
res *= (s - i);
}
return res;
}
public int numDupDigitsAtMostN(int n) {
if (n <= 10) {
return 0;
}
return n - dp(n);
}
}
233
class Solution {
static int N = 10;
//f[i][j]: i位数,最高位为j,所能得到的数当中数字1的数量
static final int[][] f = new int[N + 1][N];
static {
f[1][1] = 1;
for (int i = 2; i <= 10; i++) {
for (int j = 0; j < 10; j++) {
for (int k = 0; k < 10; k++) {
f[i][j] += f[i - 1][k];
}
if (j == 1) {
f[i][j] += pow(i - 1);
}
}
}
// for (int i = 0; i < f.length; i++) {
// System.out.println(Arrays.toString(f[i]));
// }
}
static int pow(int n) {
return (int)Math.pow(10, n);
}
public int countDigitOne(int n) {
if (n == 0) {
return 0;
}
int[] bits = new int[10];
int len = 0;
while (n > 0) {
bits[len++] = n % 10;
n /= 10;
}
int res = 0;
//右边界上的1的数量
int last = 0;
for (int i = len - 1; i >= 0; i--) {
int x = bits[i];
int j = i == len - 1 ? 1 : 0;
for (; j < x; j++) { //不包含前导0
res += f[i + 1][j];
}
res += last * x * pow(i);
if (x == 1) {
last++;
}
if (i == 0) {
res += last;
}
}
//不足N位的直接求
for (int i = 1; i < len; i++) {
for (int j = 1; j <= 9; j++) {
res += f[i][j];
}
}
return res;
}
}
bits[len++] = n % 10;
n /= 10;
} int res = 0;
//右边界上的1的数量
int last = 0;
for (int i = len - 1; i >= 0; i--) {
int x = bits[i];
int j = i == len - 1 ? 1 : 0;
for (; j < x; j++) { //不包含前导0
res += f[i + 1][j];
}
res += last * x * pow(i);
if (x == 1) {
last++;
}
if (i == 0) {
res += last;
}
}
//不足N位的直接求
for (int i = 1; i < len; i++) {
for (int j = 1; j <= 9; j++) {
res += f[i][j];
}
}
return res;
}
}