时间序列分析：ARIMA 模型（Python实践）

全文共 25000 余字，预计阅读时间约 50~83.33 分钟 | 满满干货，建议收藏！

1. ARIMA 模型的由来

首先，我们要了解为什么需要把 AR 模型和 MA 模型合并为 ARIMA 模型。这就需要我们从这两种模型的优缺点出发。

AR 模型，即自回归模型，其优势是对于具有较长历史趋势的数据，AR 模型可以捕获这些趋势，并据此进行预测。但是 AR 模型不能很好地处理某些类型的时间序列数据，例如那些有临时、突发的变化或者噪声较大的数据。AR 模型相信 “历史决定未来”，因此很大程度上忽略了现实情况的复杂性、也忽略了真正影响标签的因子带来的不可预料的影响。

相反地，MA 模型，即移动平均模型，可以更好地处理那些有临时、突发的变化或者噪声较大的时间序列数据。但是对于具有较长历史趋势的数据，MA 模型可能无法像 AR 模型那样捕捉到这些趋势。MA 模型相信 “时间序列是相对稳定的，时间序列的波动是由偶然因素影响决定的”，但现实中的时间序列很难一直维持“稳定” 这一假设。

基于以上两个模型的优缺点，我们引入了 ARIMA 模型，这是一种结合了 AR 模型和 MA 模型优点的模型，可以处理更复杂的时间序列问题。

2. ARIMA 模型的基本概念

2.1 ARIMA 模型的基本思想

ARIMA 模型全称为自回归差分移动平均模型（Autoregressive Integrated Moving Average Model）。ARIMA 模型主要由三部分构成，分别为自回归模型（AR）、差分过程（I）和移动平均模型（MA）。

ARIMA 模型的基本思想是利用数据本身的历史信息来预测未来。一个时间点上的标签值既受过去一段时间内的标签值影响，也受过去一段时间内的偶然事件的影响，这就是说，ARIMA 模型假设：标签值是围绕着时间的大趋势而波动的，其中趋势是受历史标签影响构成的，波动是受一段时间内的偶然事件影响构成的，且大趋势本身不一定是稳定的

简而言之，ARIMA 模型就是试图通过数据的自相关性和差分的方式，提取出隐藏在数据背后的时间序列模式，然后用这些模式来预测未来的数据。其中：

1、AR 部分用于处理时间序列的自回归部分，它考虑了过去若干时期的观测值对当前值的影响。

2、I 部分用于使非平稳时间序列达到平稳，通过一阶或者二阶等差分处理，消除了时间序列中的趋势和季节性因素。

3、MA 部分用于处理时间序列的移动平均部分，它考虑了过去的预测误差对当前值的影响。

结合这三部分，ARIMA 模型既可以捕捉到数据的趋势变化，又可以处理那些有临时、突发的变化或者噪声较大的数据。所以，ARIMA 模型在很多时间序列预测问题中都有很好的表现。

2.2 ARIMA 模型的数学表达式

先回顾一下 AR 和 MA 模型的数学表达式：

：

$$AR：Y_t=c+{\phi }_1{Y}_{t-1}+{\phi }_2{Y}_{t-2}+...+{\phi }_p{Y}_{t-p}+{\xi }_t\text{\hspace{1em}(1)}$$

$$MA：Y_t=\mu +{ϵ}_t+{\theta }_1{ϵ}_{t-1}+{\theta }_2{ϵ}_{t-2}+\cdots +{\theta }_q{ϵ}_{t-q}\text{\hspace{1em}(2)}$$

如果我们暂时不考虑差分（即假设 d=0），那么 ARIMA 模型可以被看作是 AR 模型和 MA 模型的直接结合，形式上看，ARIMA 模型的公式可以表示为：

$$Y_t=c+{\phi }_1{Y}_{t-1}+{\phi }_2{Y}_{t-2}+...+{\phi }_p{Y}_{t-p}+{\theta }_1{ϵ}_{t-1}+{\theta }_2{ϵ}_{t-2}+...+{\theta }_q{ϵ}_{t-q}+{ϵ}_t\text{\hspace{1em}(3)}$$

在这个公式中：

• $Y_t$Y_t 是我们正在考虑的时间序列数据。
• 到${\phi }_1到{\phi }_p$是 AR 模型的参数，这些参数用来描述当前值与过去 p 个时间点值之间的关系。
• 到${\theta }_1到{\theta }_q$ 是 MA 模型的参数，这些参数用来描述当前值与过去 q 个时间点的误差之间的关系。
• 是${\epsilon }_t是$是 在 t 时间点的误差项。
• c 是一个常数项。

这个公式基本上是将 AR 模型和 MA 模型的公式组合在一起：

1、AR 部分（即 ${\phi }_1{Y}_{t-1}+{\phi }_2{Y}_{t-2}+...+{\phi }_p{Y}_{t-p}$表示当前值 $Y_t$ 与它过去的值有关，这个部分的形式与 AR 模型的公式一致。

2、MA 部分（即 ${\theta }_1{ϵ}_{t-1}+{\theta }_2{ϵ}_{t-2}+...+{\theta }_q{ϵ}_{t-q}$表示当前值 $Y_t$与它过去的误差项有关，这个部分的形式与 MA 模型的公式一致。

值得注意的是，MA 模型中代表长期趋势的均值 $\mu$ 并不存在于 ARIMA 模型的公式当中，因为 ARIMA 模型中 “预测长期趋势” 这部分功能由 AR 模型来执行，因此 AR 模型替代了原本的 $\mu$ 。在 ARIMA 模型中，c 可以为 0。

另外，这个公式的基础是假设我们正在处理的时间序列是平稳的，这样我们可以直接应用 AR 和 MA 模型。如果时间序列是非平稳的，那么我们就需要考虑 ARIMA 模型中的 I 部分，也就是进行差分处理。

上述模型被称之为 ARIMA(p,d,q) 模型，其中 p 和 q 的含义与原始 MA、AR 模型中完全一致，且 p 和 q 可以被设置为不同的数值，而 d 是 ARIMA 模型需要的差分的阶数，下面要重点讲解的参数，请继续往下看。

3. 差分过程（I）的详解

3.1 什么是差分

差分是一种数学操作，用于计算一组数值序列中相邻数据点的差值。在时间序列分析中，差分常用于将非平稳序列转化为平稳序列，也就是减小或消除时间序列的趋势和季节性变化。

当我们对一个序列进行差分运算，就意味着我们会计算该序列中的不同观测值之间的差异

简单地说，如果我们有一个时间序列 $Y_t$ ，那么该序列的一阶差分就可以定义为：

$$\Delta Y_t=Y_t-Y_{t-1}\text{\hspace{1em}(4)}$$

这样，我们得到一个新的时间序列，其每一个值都是原时间序列中相邻两个值的差。

让我们以一个简单的例子来具体理解理解差分操作：

假设我们有以下一组时间序列数据：

$$Y=4,8,6,5,3,4\text{\hspace{1em}(5)}$$

我们可以看到，这个序列的长度是 6。现在，我们希望对这个序列进行一阶差分。

第一步，我们计算第二个数据点和第一个数据点的差，也就是 8-4=4。

第二步，我们计算第三个数据点和第二个数据点的差，也就是 6-8=-2。

依次类推，我们计算出所有相邻数据点之间的差值，得到一个新的序列：

$$\Delta Y=4,-2,-1,-2,1\text{\hspace{1em}(6)}$$

我们可以看到，差分后的序列比原序列短了一位，因为差分操作实际上计算的是原序列中的相邻数据点之间的差值。同时，差分后的序列相比于原序列，其趋势和季节性变化都得到了一定程度的消除。通常进行一次差分运算，原始的序列会变短 1 个单位。

在实际进行差分运算时，我们可以改变差分运算的两个相关因子来执行不同的差分：一个是差分的阶数（order），另一个是差分的滞后（lag）。

3.2 差分的阶数

在上一节，我们介绍了一阶差分。然而，实际上，差分的阶数可以是任何正整数。差分的阶数就是我们需要进行多少次差分操作才能得到一个平稳序列。

具体地说，二阶差分就是对一阶差分后的序列再次进行差分。如果我们有一个时间序列 $Y_t$，那么该序列的二阶差分就可以定义为：

$${\Delta }^2{Y}_t=\Delta (Y_t-Y_{t-1})=(Y_t-Y_{t-1})-(Y_{t-1}-Y_{t-2})=Y_t-2Y_{t-1}+Y_{t-2}\text{\hspace{1em}(7)}$$

这样，我们得到一个新的时间序列，其每一个值都是原时间序列中相邻两个值的差的差。

让我们以一个简单的例子来具体理解高阶差分操作：

假设我们有以下一组时间序列数据：

$$Y=4,8,6,5,3,4\text{\hspace{1em}(8)}$$

首先，我们进行一阶差分，就像我们之前讲解的，具体的计算步骤如下：

1. 计算第二个数据点和第一个数据点的差，也就是 8-4=4。
2. 计算第三个数据点和第二个数据点的差，也就是 6-8=-2。
3. 以此类推，我们计算出所有相邻数据点之间的差值。

所以，一阶差分的结果如下：

$$\Delta Y=4,-2,-1,-2,1\text{\hspace{1em}(9)}$$

然后，我们对这个一阶差分序列进行二阶差分。同样，我们从头开始计算相邻数据点的差值：

1. 计算第二个数据点和第一个数据点的差，也就是 (-2)-4=-6。
2. 计算第三个数据点和第二个数据点的差，也就是 (-1)-(-2)=1。
3. 以此类推，我们计算出所有相邻数据点之间的差值。

所以，二阶差分的结果如下：

$${\Delta }^{2}Y=-6,1,-1,3\text{\hspace{1em}(10)}$$

我们可以看到，二阶差分后的序列比一阶差分的序列又短了一位。实际上是需要对序列 Y 进行两次一阶差分，

因此，n 阶差分就是在原始数据基础上进行 n 次一阶差分。在现实中，我们使用的高阶差分一般阶数不会太高。在 ARIMA 模型中，超参数 $d$ 最常见的取值是 0、1、2 这些很小的数字。

3.3 什么是滞后

在时间序列分析中，“滞后” 是一个非常重要的概念。滞后实际上是描述了时间序列数据点之间的时间差。举个例子，对于一个月度数据的时间序列， 就代表了 $Y_{t-1}就代表了Y_t$就代表了 Y_t 的一个月的滞后。

差分的滞后（lag）与差分的阶数完全不同。正常的一阶差分是滞后为 1 的差分（lag-1 Differences），这代表在差分运算中，我们让相邻的两个观测值相减，即让间隔为（lag-1）的两个观测值相减。因此，当滞后为 2 时，则代表我们需要让相隔 1 个值的两个观测值相减。

在 ARIMA 模型中，我们经常需要计算滞后 d 期的时间序列数据。这就意味着我们需要查找在 t 时刻前 d 个时间单位的数据。

让我们通过一个具体的例子来了解如何进行滞后操作。

假设我们有以下一组时间序列数据：

$$Y=4,8,6,5,3,4\text{\hspace{1em}(11)}$$

如果我们想要计算这个时间序列的一阶滞后序列，我们只需要将原序列向右移动一个单位，然后删除掉移动后超出的数据点，具体操作如下：

1. 我们先将整个序列向右移动一个单位，得到 {_, 4, 8, 6, 5, 3, 4}。
2. 然后，我们删除掉移动后超出的数据点，得到滞后序列 {4, 8, 6, 5, 3}。

如果我们想要计算二阶滞后序列，我们可以按照同样的方式进行操作：

1. 我们先将一阶滞后序列再向右移动一个单位，得到 {, , 4, 8, 6, 5, 3}。
2. 然后，我们删除掉移动后超出的数据点，得到二阶滞后序列 {4, 8, 6, 5}。

通过以上的操作，我们可以得到任意阶的滞后序列。

3.4 滞后差分（多步差分）

滞后差分（Lag Differences）是在进行差分操作时，不是用相邻的观测值进行相减，而是用相隔一定数量（即滞后数量）的观测值进行相减。这种操作通常在时间序列具有周期性的情况下非常有用，例如，当我们处理的数据随季节有规律地波动或者随一周的时间有规律地波动时。

让我们以一个简单的例子来具体理解滞后差分的操作：

假设我们有一个时间序列：

$$X=[5,4,6,7,9,12]\text{\hspace{1em}(12)}$$

现在，我们想要计算这个时间序列的 2 步滞后差分（lag-2 Differences）序列。首先，我们让相隔 1 个值的两个观测值相减，具体操作如下：

1. 首先，我们对序列进行滞后 2 差分运算，即进行 6-5、7-4、9-6、12-7 的运算。
2. 最终我们得到的新的时间序列：

$$X_{la{g}_2}=[1,3,3,5]\text{\hspace{1em}(13)}$$

通过这个例子，我们可以看出滞后差分的操作就是令序列中索引更大的值减去与其相隔（lag-1）个样本的索引更小的值。在实际操作中，我们可以根据数据的特性，选择合适的滞后阶数，来对数据进行滞后差分操作。

带滞后的差分也叫做多步差分，例如，滞后为 2 的差分就叫做 2 步差分。相比起平时不怎么使用的高阶差分，多步差分应用非常广泛。在时间序列中，标签往往具备一定的周期性：例如，标签可能随季节有规律地波动（比如在夏季标签值高、在冬季标签值较低等），也可能随一周的时间有规律地波动（比如在周末较高、在工作日较低等）

3.5 使用差分消除数据波动

在时间序列中，标签往往具备一定的周期性：例如，标签可能随季节有规律地波动（比如在夏季标签值高、在冬季标签值较低等），也可能随一周的时间有规律地波动（比如在周末较高、在工作日较低等）。这种波动可以通过滞后差分来消除，我们生成一个人造的不平稳时间序列，并通过差分使其平稳。我们将利用 Numpy 和 Pandas 库生成这个序列，然后用同样的步骤进行检验和可视化。代码如下：

# 导入必要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller

# 创建一个函数来检查数据的平稳性
def test_stationarity(timeseries):
    # 执行Dickey-Fuller测试
    print('Results of Dickey-Fuller Test:')
    dftest = adfuller(timeseries, autolag='AIC')
    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic', 'p-value', '#Lags Used', 'Number of Observations Used'])
    for key, value in dftest[4].items():
        dfoutput['Critical Value (%s)' % key] = value
    print(dfoutput)

# 生成不平稳的时间序列
np.random.seed(0)
n = 100
x = np.cumsum(np.random.randn(n))

# 把它转换成Pandas的DataFrame格式
df = pd.DataFrame(x, columns=['value'])

# 检查原始数据的平稳性
test_stationarity(df['value'])

# 进行一阶差分
df['first_difference'] = df['value'] - df['value'].shift(1)

# 检查一阶差分后的数据的平稳性
test_stationarity(df['first_difference'].dropna())

# 进行二阶差分
df['second_difference'] = df['first_difference'] - df['first_difference'].shift(1)

# 检查二阶差分后的数据的平稳性
test_stationarity(df['second_difference'].dropna())

# 可视化原始数据和差分后的数据
plt.figure(figsize=(12, 6))
plt.plot(df['value'], label='Original')
plt.plot(df['first_difference'], label='1st Order Difference')
plt.plot(df['second_difference'], label='2nd Order Difference')
plt.legend(loc='best')
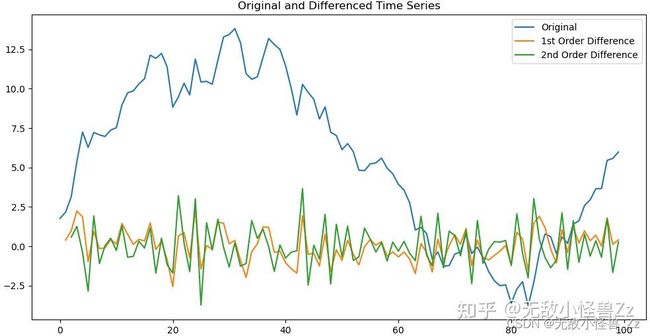
plt.title('Original and Differenced Time Series')
plt.show()

这段代码首先创建了一个不平稳的时间序列。然后，它对原始数据、一阶差分数据和二阶差分数据进行了平稳性检验。最后，它画出了原始数据以及一阶和二阶差分数据的图形。

在你运行这段代码之后，你应该会看到，原始数据不平稳，一阶差分后的数据仍然不完全平稳，而二阶差分后的数据就已经变得平稳了。

从图像上可以看出，已经成功展示了如何通过多步差分将一个非平稳时间序列转换为平稳时间序列。

我们更具体的分析，执行上述代码后，输出如下：

Results of Dickey-Fuller Test:
Test Statistic                 -1.132038
p-value                         0.702128
#Lags Used                      0.000000
Number of Observations Used    99.000000
Critical Value (1%)            -3.498198
Critical Value (5%)            -2.891208
Critical Value (10%)           -2.582596
dtype: float64
Results of Dickey-Fuller Test:
Test Statistic                -9.158402e+00
p-value                        2.572287e-15
#Lags Used                     0.000000e+00
Number of Observations Used    9.800000e+01
Critical Value (1%)           -3.498910e+00
Critical Value (5%)           -2.891516e+00
Critical Value (10%)          -2.582760e+00
dtype: float64
Results of Dickey-Fuller Test:
Test Statistic                 -5.459820
p-value                         0.000003
#Lags Used                     11.000000
Number of Observations Used    86.000000
Critical Value (1%)            -3.508783
Critical Value (5%)            -2.895784
Critical Value (10%)           -2.585038
dtype: float64

原始数据：Dickey-Fuller 检验的 p 值为 0.702128，这个值大于常用的显著性水平（例如 0.05 或 0.01）。这意味着我们无法拒绝原假设（时间序列是非平稳的）。因此，我们可以确认原始数据是非平稳的。

一阶差分数据：一阶差分后，p 值为 2.572287e-15（接近于 0），远小于 0.05 或 0.01，我们可以拒绝原假设（时间序列是非平稳的），因此我们可以认为一阶差分后的数据是平稳的。

二阶差分数据：二阶差分后，p 值为 0.000003，也是远小于 0.05 或 0.01，我们也可以拒绝原假设（时间序列是非平稳的），我们可以认为二阶差分后的数据是平稳的。

因此，从上述结果来看，一阶差分已经足够使数据平稳。这就表明了差分的作用：它可以帮助我们把一个非平稳的时间序列转换成平稳的时间序列，从而更好地进行进一步的时间序列分析或预测。

至于你的图形，可以看到：原始数据是典型的非平稳时间序列的特征。一阶差分后的数据虽然波动减小，但还是有一些非常规波动。二阶差分后的数据在 0 附近波动，看起来更像是一个平稳的时间序列。

差分运算可以消除数据中激烈的波动，因此可以消除时间序列中的季节性、周期性、节假日等影响。一般我们使用滞后为 7 的差分消除星期的影响，而使用滞后为 12 的差分来消除月份的影响（一般这种情况下每个样本所对应的时间单位是月），我们也常常使用滞后 4 来尝试消除季度所带来的影响。在统计学中，差分运算本质是一种信息提取方式，其最擅长提取的关键信息就是数据中的周期性，和其他信息提取方式一样，它会舍弃部分信息、提炼出剩下的信息供模型使用。也因此，差分最重要的意义之一就是能够让带有周期性的数据变得平稳.

3.6 概念总结

上述这么多概念，是不是有点懵？没关系，我们来总结一下：

当我们谈论时间序列分析中的 “差分”、“滞后差分” 和 “多步差分” 时，我们通常是在谈论同一种基本概念，即比较一个时间序列在不同时间点的值。然而，这些术语的具体含义可能会根据上下文有所不同。让我为你详细解释一下：

1、差分（Differencing）：这是一种预处理技术，用于使非平稳时间序列变得平稳。在时间序列中进行一阶差分，就是将每个观察值与其前一步的观察值进行比较，然后取这两个观察值之间的差异。例如，如果我们有一个时间序列 $x1,x2,x3,...,xn${x1, x2, x3, …, xn} ，那么一阶差分序列将是 $x2-x1,x3-x2,...,xn-xn-1${x2 - x1, x3 - x2, …, xn - xn-1} 。

2、滞后差分（Lagged Differencing）：这个术语和 “差分” 非常相似。当我们说 “滞后” 时，我们是在说比较一个观察值和其 “前一步” 或 “几步前” 的观察值。因此，“滞后一阶差分” 实际上就是常规的一阶差分，因为我们比较的是每个观察值与其前一步的观察值。如果我们进行的是 “滞后 k 阶差分”，那么我们比较的是每个观察值与其 k 步前的观察值。

3、n 阶差分（n-th Order Differencing）：n 阶差分是差分的一种更一般的形式。一阶差分是比较每个观察值与其前一步的观察值，二阶差分是对一阶差分序列进行再一次的差分（也就是比较一阶差分序列中的每个值与其前一步的值）。更一般地，n 阶差分就是连续进行 n 次一阶差分。

4、多步差分（Multi-step Differencing）：这个术语可能根据上下文有不同的含义。它可能指的是 n 阶差分（即进行多次连续的一阶差分）。也可能指的是滞后差分，比如比较每个观察值与其几步前的观察值。

4. ARIMA(p,d,q) 模型的参数选择

4.1 p 和 q 到底是什么

在 ARIMA(p, d, q) 模型中：

p 代表 “自回归部分 (Autoregressive)”： 这部分描述了模型中使用的观测值的滞后值（即前面 p 个期的值）。自回归模型的出发点是认为观测值是它前面的 p 个值的线性组合。具体的数学形式如下：

：

$$AR：Y_t=c+{\phi }_1{Y}_{t-1}+{\phi }_2{Y}_{t-2}+...+{\phi }_p{Y}_{t-p}+{\xi }_t\text{\hspace{1em}(14)}$$

其中， ${ϵ}_{t-1},{ϵ}_{t-2},...,{ϵ}_{t-q}$ 是模型参数，c 是常数， ${\xi }_t$是白噪声。这个方程的阶数 p 决定了模型回溯观测值的数量。

q 代表 “移动平均部分 (Moving Average)”：这部分描述了模型中使用的错误项的滞后值（即前面 q 个期的值）。移动平均模型是将当前值和过去的白噪声之间建立关系。具体的数学形式如下：

：

$$MA：Y_t=\mu +{ϵ}_t+{\theta }_1{ϵ}_{t-1}+{\theta }_2{ϵ}_{t-2}+\cdots +{\theta }_q{ϵ}_{t-q}\text{\hspace{1em}(15)}$$

其中， ${\theta }_1,{\theta }_2,...,{\theta }_q$ 是模型参数，c 是常数，$e_t$ 是当前时期的白噪声， ${ϵ}_{t-1},{ϵ}_{t-2},...,{ϵ}_{t-q}$ 是过去的白噪声。这个方程的阶数 q 决定了模型回溯白噪声的数量。

因此，ARIMA 模型将自回归模型（AR）和移动平均模型（MA）结合在一起，同时加入了差分（I）这个操作。而 p, d, q 这三个参数，分别代表了模型中的自回归部分、差分阶数、以及移动平均部分。

4.2 d 到底是什么

d 就是差分的阶数。差分的目标是将非平稳序列转变为平稳序列。具体的数学表达如下：

滞后运算是 “向后移动一个单位” 的运算，当用于时间序列时，它特指 “向过去移动一个时间单位” 的运算。大部分时候，滞后运算被简写为字母 B（Backshift）或者字母 L（Lag），我们可以对单一的时序样本或整个时间序列做滞后运算。假设有一时间序列 $y_t$ 定义滞后运算（lag operator）B，它将一个时刻的观测值转化为前一时刻的观测值：

$$B{y}_t=y_{t-1}\text{\hspace{1em}(16)}$$

我们可以扩展这个运算符的概念，使之滞后 n 个时间步长。例如：

$$B^n{y}_t=y_{t-n}\text{\hspace{1em}(17)}$$

此外，我们可以利用滞后运算来表示一阶差分和 n 阶差分。一阶差分可以看做是相邻的标签值之间的差，它可以表示为：

$$\Delta y_t=y_t-y_{t-1}=y_t-B{y}_t=(1-B)y_t\text{\hspace{1em}(18)}$$

类似的，n 阶差分就是相隔 n-1 个标签值进行相减：

$${\Delta }^n{y}_t=y_t-y_{t-n}=y_t-B^n{y}_t=(1-B^n)y_t\text{\hspace{1em}(19)}$$

这个式子告诉我们，如果我们想对一组数据进行 n 阶差分，那么我们就可以使用滞后运算。

同时，我们还可以利用滞后运算来表示高阶差分。如果我们对时间序列进行两次一阶差分，那么我们就得到了二阶差分。二阶差分可以表述为：

$${\Delta }^2{y}_t=\Delta (\Delta y_t)=(y_t-y_{t-1})-(y_{t-1}-y_{t-2})=y_t-2y_{t-1}+y_{t-2}=(1-2B+B^2)y_t=(1-B{)}^2{y}_t\text{\hspace{1em}(20)}$$

这个式子告诉我们，如果我们想对一组数据进行二阶差分，那么我们可以直接对原始数据应用滞后运算符。

以此类推，d 阶差分可以被表示为：

$$d\_order\_y=(1-B{)}^d{y}_t\text{\hspace{1em}(21)}$$

一般来说，ARIMA 模型中的 d 代表的就是这样的差分阶数。当我们在 ARIMA 模型中设定 d 等于一个特定的数值时，我们实际上是在告诉模型，我们应用了多少次滞后运算（也就是进行了多少次差分）来使数据变得平稳。这就是为什么在进行 ARIMA 模型拟合前，我们需要先通过画图或者 ADF 检验等方式，确定最小的 d 使得数据平稳。在确定了 d 之后，我们就可以将 d 阶差分后的序列代入模型进行拟合。

上面的推导，可以帮助我们理解 ARIMA(p, d, q) 中的 d 是如何通过滞后运算与差分建立起来的关系，以及它是如何影响我们的模型的。

在实际使用中，我们经常将多步差分和高阶差分混用，最典型的就是在 ARIMA 模型建模之前：一般我们会先使用多步差分令数据满足 ARIMA 模型的基础建模条件，再在 ARIMA 模型中使用低阶的差分帮助模型更好地建模。例如，先对数据进行 12 步差分、再在模型中进行 1 阶差分，这样可以令数据变得平稳的同时、又提取出数据中的周期性，极大地提升模型对数据的拟合精度。

5. ACF 与 PACF

5.1 时序数据的平稳性

当我们说一个时间序列是平稳的，基本上意味着其统计特性（如均值，方差）在时间上是常数或不会随时间变化。平稳性是 ARIMA 模型所假设的关键特性，因为模型的预测能力在很大程度上取决于这个假设。

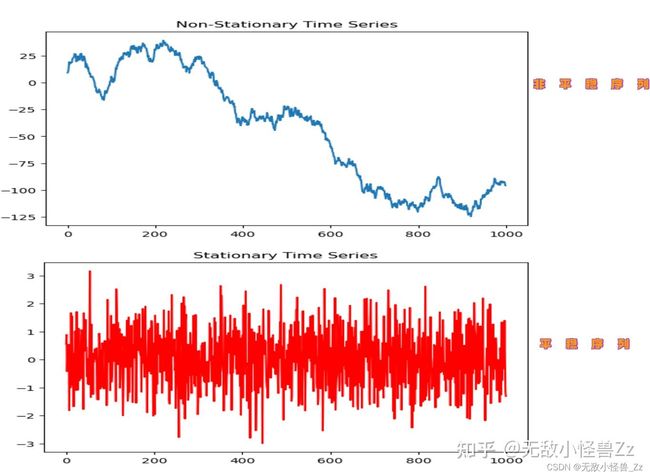
我们生成 1000 个数据点的平稳和非平稳时间序列。在非平稳序列中，我们增加了一个正弦项，以产生更明显的波动。这样，就可以看到一个具有明显周期性和变化幅度的非平稳序列

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 设置随机种子以确保结果可重复
np.random.seed(0)

# 生成平稳时间序列
stationary = np.random.normal(loc=0, scale=1.0, size=1000)
s_ts = pd.Series(stationary)
s_ts.plot()
plt.title('Stationary Time Series')
plt.show()

# 生成非平稳时间序列
non_stationary = np.cumsum(np.random.normal(loc=0, scale=2.0, size=1000)) + 10 * np.sin(np.linspace(-10, 10, 1000))
ns_ts = pd.Series(non_stationary)
ns_ts.plot()
plt.title('Non-Stationary Time Series')
plt.show()

在第一幅图中，我们看到的序列有一个明显的周期性波动模式。这个序列的均值和方差都在随时间变化。均值在随时间变化是因为我们在生成这个序列时，将随机数进行了累加；方差在随时间变化是因为我们增加了一个正弦项，使得序列在不同的时间点具有不同的波动幅度。这些性质都违反了平稳时间序列的定义，所以我们称这个序列为非平稳时间序列。

在第二幅图中，我们可以看到序列在 0 附近随机波动。这个序列的均值和方差都是常数。均值是因为我们在生成这个序列时，从均值为 0 的正态分布中抽取了随机数；方差也是常数，因为这些随机数是独立同分布的。这些性质都满足平稳时间序列的定义，所以我们称这个序列为平稳时间序列。

在时间序列分析中，我们通常需要将非平稳时间序列转化为平稳时间序列，因为许多时间序列模型（如 AR、MA 和 ARIMA 模型）都假设输入的数据是平稳的。这种转化可以通过差分或其他预处理方法来实现。

ACF (Auto-Correlation Function) 和 PACF (Partial Auto-Correlation Function) 是时间序列分析中的两个重要工具，它们可以用来检验一个时间序列是否是平稳的，以及帮助确定 ARIMA 模型的参数。

5.2 自相关函数 ACF (Auto-Correlation Function)

在深入理解 ACF 之前，我们先来理解一下 “相关性” 的基本概念。一般来说，“相关性” 用于衡量两个变量之间的线性关系。对于时间序列数据，这两个变量通常是在不同时间点的观测值。例如，假设我们有以下一组观测值：[3, 5, 4, 6, 7, 8, 7, 6, 5, 4, 3]，我们可能会问，第 t 个观测值与第 t-1 个观测值有多大的相关性？这时，我们就需要用到自相关系数（ACF）来衡量。

在实际应用中，ACF 通常被定义为当前时间点上的观测值与历史时间点观测值之间的相关性。这种相关性可以用多种方法来衡量，其中最常用的是皮尔逊相关系数。

这是一个相对宽泛的定义，而在时间序列分析中，ACF 有着更为严格的定义。对于任意的滞后（lag）k，我们都计算出在时间 t 和时间 t+k 的数据点之间的协方差，然后除以该时间序列的方差。这样得到的结果反映了时间序列自身的相关性。

数学上，自相关函数（ACF）的定义如下：

如果我们有一个时间序列 {X_t}，那么对于任意的滞后（lag）k，自相关函数 ρ(k) 可以表示为：

$$\rho (k)=Cov(X_t,X_{t+k})/Var(X_t)\text{\hspace{1em}(22)}$$

其中， $Cov(X_t,X_{t+k})$是时间点 t 和时间点 t+k 的观测值的协方差， $Var(X_t)$ 是时间序列 $X_t$ 的方差。

ACF 的取值范围是 -1 到 1。当 ACF 接近 1 时，表示两个时间点的观测值高度正相关；当 ACF 接近 -1 时，表示两个时间点的观测值高度负相关；当 ACF 接近 0 时，表示两个时间点的观测值之间的相关性较弱。

通过计算不同滞后值下的 ACF，我们可以得到一个关于滞后的函数，这就是自相关函数。我们通常使用自相关图（ACF 图）来直观地表示这个函数，这将在后面的内容中详细介绍。

5.3 偏自相关函数（Partial Auto-correlation Function， PACF）

在理解 PACF 之前，我们需要先理解什么是 “直接相关性”。直接相关性是指一个变量与另一个变量之间的相关性，而不考虑其他变量的影响。例如，假设我们有以下一组观测值：[3, 5, 4, 6, 7, 8, 7, 6, 5, 4, 3]，我们可能会问，第 t 个观测值与第 t-2 个观测值之间有多大的直接相关性，而这个直接相关性并没有考虑第 t-1 个观测值的影响。这时，我们就需要用到偏自相关系数（PACF）来衡量。

在时间序列分析中，偏自相关函数（PACF）衡量的是在其他更早期的滞后（lag）观测值已经被考虑后，当前时间点的观测值与某个滞后观测值之间的 “直接相关性”。换句话说，PACF 表示的是两个观测值之间的相关性，去掉其他滞后观测值的影响。

数学上，偏自相关函数（PACF）的定义如下：

如果我们有一个时间序列 {X_t}，那么对于任意的滞后（lag）k，偏自相关函数 φ(k) 可以表示为：

$$\phi (k)=Cov(X_t-E[X_t|X_{t-1},...,X_{t-k+1}],X_{t-k}-E[X_{t-k}|X_{t-k+1},...,X_{t-1}])/Var(X_t)\text{\hspace{1em}(23)}$$

其中，Cov 表示协方差，E 表示期望，也就是平均值，Var 表示方差。我们可以看到，PACF 的计算过程实际上是先去掉其他更早期的滞后观测值的影响，然后再计算相关性。

PACF 的取值范围也是 -1 到 1。当 PACF 接近 1 时，表示两个时间点的观测值高度正相关；当 PACF 接近 -1 时，表示两个时间点的观测值高度负相关；当 PACF 接近 0 时，表示两个时间点的观测值之间的直接相关性较弱。

通过计算不同滞后值下的 PACF，我们可以得到一个关于滞后的函数，这就是偏自相关函数。我们通常使用偏自相关图（PACF 图）来直观地表示这个函数，这将在后面的内容中详细介绍。

5.4 ACF 和 PACF 计算示例

对于自相关系数（ACF）和偏自相关系数（PACF），一开始可能会感觉有些难以理解。以下是一个更加详细的例子，希望能帮助你更好地理解。

假设我们有以下一组观测值：X = [3, 5, 4, 6, 7, 8, 7, 6, 5, 4, 3]，使用自相关系数（ACF）的计算第 t 个观测值 $X_t$ 与第 t-2 个观测值 $X_{t-2}$ 的自相关系数。这里，我们只需要关注当前观测值和滞后 2 的观测值，不需要考虑滞后 1 的观测值。所以，我们可以使用以下公式计算 ACF：

$$ACF(2)=Cov(X_t,X_{t-2})/sqrt(Var(X_t)\ast Var(X_{t-2}))\text{\hspace{1em}(24)}$$

那如果使用偏自相关系数 PACF 的计算第 t 个观测值 $X_t$与第 t-2 个观测值 $X_{t-2}$ 的偏自相关系数。与自相关系数的计算不同，这里我们需要考虑其他更早期的滞后观测值的影响。所以，我们需要使用以下公式计算 PACF：

$$PACF(2)=Cov(X_t-E[X_t|X_{t-1}],X_{t-2}-E[X_{t-2}|X_{t-1}])/sqrt(Var(X_t)\ast Var(X_{t-2}))\text{\hspace{1em}(25)}$$

其中，Cov 表示协方差，E 表示期望，也就是平均值，Var 表示方差。我们首先去掉 和对 $X_t和X_{t-2}对X_{t-1}$ 的条件期望，然后再计算剩下的部分的协方差，最后除以 $X_t$和 $X_{t-2}$的方差的乘积的平方根。

可以看到，偏自相关系数的计算过程要复杂一些，因为我们需要考虑其他更早期的滞后观测值的影响。但这也使得偏自相关系数能够更好地衡量当前观测值和滞后观测值之间的 “直接相关性”。

让我们换一种更通俗的方式来理解 ACF 和 PACF。

假设我们在观察一个湖泊的水温。假设我们每天都在固定的时间测量水温，并记录下来

1、 自相关系数（ACF）： 自相关就好比我们在考虑 “今天的水温是否会受到昨天水温的影响？” 如果昨天的水温很高，那么今天的水温可能也会偏高。这种相互影响可以用自相关系数来衡量。换句话说，自相关系数可以帮助我们理解在时间序列中，一个时间点的值如何影响另一个时间点的值。

2、偏自相关系数（PACF）： 偏自相关在这个例子中，可以被理解为 “在已知昨天水温的情况下，今天的水温还会受到前天水温的影响吗？” 也就是说，我们在计算今天和前天的水温关系时，已经考虑并剔除了昨天水温的影响。这种关系被称为 “偏自相关”。

用这种方式理解，我们可以更直观地看到 ACF 和 PACF 的区别。ACF 是直接考虑相邻两天的水温的关系，而 PACF 是在已知昨天水温的情况下，考虑今天和前天的水温的关系。

在实际应用中，我们通常使用相关的统计软件来计算 ACF 和 PACF，而不需要手动计算。所以理解就好。

5.5 ACF 和 PACF 的图形解读

ACF 和 PACF 的取值范围都是 [-1,1]，其中 1 代表两个序列完全正相关，-1 代表两个序列完全负相关，0 代表两个序列不相关。

我们生成一个 AR(1) 模型的时间序列数据，然后使用 statsmodels 库中的 plot_acf 和 plot_pacf 函数来绘制其自相关函数（ACF）和部分自相关函数（PACF）的图像。以下是 Python 代码：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import statsmodels.api as sm

# 设置随机种子以确保结果可重复
np.random.seed(0)

# 生成AR(1)时间序列数据
ar = np.array([1, -0.5])  # 我们将使用的AR模型的参数
ma = np.array([1])  # 这是MA模型的参数，在这个例子中我们不需要它
n = int(1000)  # 我们将生成的数据点的数量

arma_process = sm.tsa.ArmaProcess(ar, ma)
y = arma_process.generate_sample(nsample=n)

# 绘制ACF图像
plot_acf(y, lags=20)
plt.title('ACF of AR(1) Time Series')
plt.show()

# 绘制PACF图像
plot_pacf(y, lags=20)
plt.title('PACF of AR(1) Time Series')
plt.show()

在这个代码中，我们首先设置了随机种子以确保结果可重复，然后定义了 AR(1) 模型的参数和我们将生成的数据点的数量。接下来，我们使用 statsmodels.tsa.ArmaProcess 对象和其 generate_sample 方法来生成 AR(1) 时间序列数据。最后，我们使用 plot_acf 和 plot_pacf 函数来绘制 ACF 和 PACF 图像。

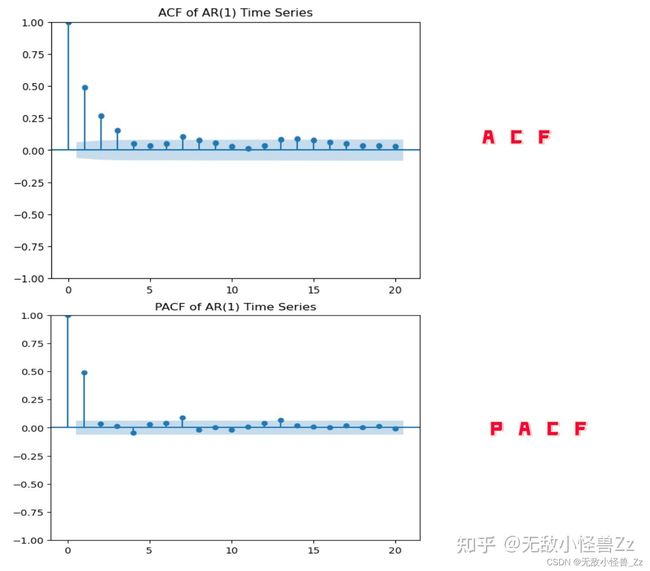
ACF 图和 PACF 图的横坐标相同，都是不同的滞后程度，纵坐标是当前滞后程度下序列的 ACF 和 PACF 值。背景为蓝色的区域代表着 95% 或 99% 的置信区间，当 ACF/PACF 值在蓝色区域之外时，我们就认为当前滞后程度下的 ACF/PACF 是统计上显著的值，即这个滞后程度下的序列之间的相关性很大程度上是信任的、不是巧合。需要注意的是，当滞后为 0 时，ACF 和 PACF 值必然为 1，因为一个序列与自己始终完全相关，因此 ACF 和 PACF 图上有意义的值是从滞后为 1 的值开始看

详细地解释一下这个过程：

AR(1) 模型是一种自回归模型，它的当前值只依赖于前一步的值。所以，对于一个 AR(1) 模型，我们有：

$$X[t]=c+\phi X[t-1]+\epsilon [t]\text{\hspace{1em}(26)}$$

其中 X[t] 是当前时间点的值，X[t-1] 是前一时间点的值，c 是常数，φ是自回归系数，ε[t] 是噪声项。

ACF 衡量的是时间序列与其自身滞后版本之间的相关性。对于 AR(1) 模型，其 ACF 应在滞后 1 时有一个峰值，然后逐渐衰减。原因是，当滞后 1 时，我们实际上在比较 X[t] 和 X[t-1]，它们是直接相关的，所以有一个峰值。而当滞后增加时，比如滞后 2 时，我们在比较 X[t] 和 X[t-2]，虽然 X[t] 和 X[t-2] 之间存在间接的关联（通过 X[t-1]），但是这种关联会随着滞后的增加而衰减。

部分自相关函数（PACF）：PACF 衡量的是时间序列与其滞后版本之间的相关性，但是要剔除中间滞后项的影响。对于 AR(1) 模型，其 PACF 应在滞后 1 时有一个峰值，然后突然降到 0。原因是，当滞后 1 时，我们实际上在比较 X[t] 和 X[t-1]，它们是直接相关的，所以有一个峰值。而当滞后增加时，比如滞后 2 时，我们在比较 X[t] 和 X[t-2]，尽管它们之间存在间接的关联，但是这种关联被 X[t-1] 的影响所剔除，所以 PACF 在滞后 2 以后的值应接近于 0。

因此，ACF 和 PACF 的图像是反映 AR(1) 模型结构的重要工具。通过它们，我们可以看出时间序列的当前值主要依赖于前一步的值，而与更早的历史值的关联性较弱。

6 实践中如何选择超参数 p、q 和 d

6.1 不同的 p、d 和 q 能决定模型类型

回顾一下：ARIMA 模型的公式可以表示为：

$$Y_t=c+{\phi }_1{Y}_{t-1}+{\phi }_2{Y}_{t-2}+...+{\phi }_p{Y}_{t-p}+{\theta }_1{ϵ}_{t-1}+{\theta }_2{ϵ}_{t-2}+...+{\theta }_q{ϵ}_{t-q}+{ϵ}_t\text{\hspace{1em}(27)}$$

上面我们已经提到过了，ARIMA 模型中的三个参数 p、q、d 分别代表的含义是：p 和 q 分别控制 ARIMA 模型中自回归和移动平均的部分，而 d 则控制输入 ARIMA 模型的数据被执行的差分的阶数。我们可以这样理解：

ARIMA(p,d,q)	模型类型	模型解释
ARIMA(0,d,0)	随机游走模型或白噪声模型	当 d=1 时，是随机游走模型；当 d=0 时，是白噪声模型
ARIMA(0,d,q)	MA 模型或 IMA 模型	当 d=0 时，是 MA(q) 模型；当 d≠0 时，是 IMA(d,q) 模型
ARIMA(p,d,0)	AR 模型或 ARIMA 模型	当 d=0 时，是 AR 模型；当 d≠0 时，是 ARIMA(p,d,0) 模型
ARIMA(p,d,q)	ARMA 模型或 ARIMA 模型	当 d=0 时，是 ARMA(p, q) 模型；当 d≠0 时，是 ARIMA(p,d,q) 模型

模型解释：

1、AR 模型（Autoregressive Model）：自回归模型，它将当前值与过去 p 个值的线性组合进行比较。

2、MA 模型（Moving Average Model）：移动平均模型，它将当前值与过去 q 个误差项的线性组合进行比较。

3、ARMA 模型（Autoregressive Moving Average Model）：自回归移动平均模型，它是 AR 模型和 MA(q) 模型的组合。

4、ARIMA 模型（Autoregressive Integrated Moving Average Model）：自回归积分移动平均模型，它是 ARMA(p, q) 模型的扩展，增加了差分的步骤，使得非平稳序列变得平稳。

5、IMA 模型（Integrated Moving Average Model）：积分移动平均模型，它是 MA(q) 模型的扩展，增加了差分的步骤，使得非平稳序列变得平稳。

6.2 超参数 p 的确定

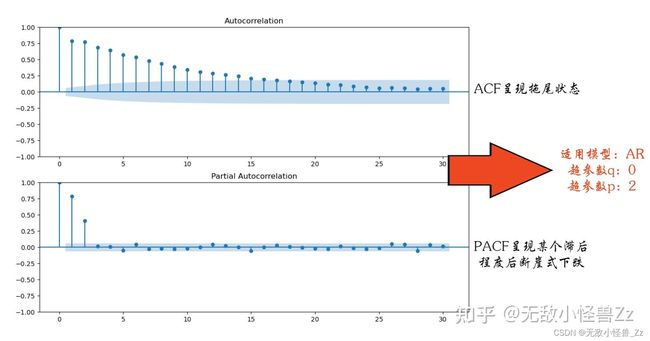
对于 AR 模型，ACF 会展现出拖尾的形式，而 PACF 则在 p 阶后突然截尾。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_process import ArmaProcess
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# 参数
ar = np.array([1, -0.5, -0.4])
ma = np.array([1])

# 生成AR(2)过程
ar2_process = ArmaProcess(ar, ma)
ar2_sample = ar2_process.generate_sample(nsample=1000)

# 绘制ACF和PACF
plt.figure(figsize=(12,8))
plt.subplot(211)
plot_acf(ar2_sample, ax=plt.gca())
plt.subplot(212)
plot_pacf(ar2_sample, ax=plt.gca())
plt.show()

对任意时间序列，当 ACF 图像呈现拖尾、且 PACF 图像呈现截尾状态时，当前时间序列适用 AR 模型，且 PACF 截尾的滞后阶数就是超参数 p 的理想值，如图：

6.3 超参数 q 的确定

对于 MA 模型，ACF 在 q 阶后突然截尾，而 PACF 则呈现拖尾的形式

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_process import ArmaProcess
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# 定义MA模型的参数
ar = np.array([1])
ma = np.array([1, 0.5, 0.7])
np.random.seed(1)

# 创建ARMA模型
arma_process = ArmaProcess(ar, ma)
sample = arma_process.generate_sample(nsample=1000)

# 绘制ACF和PACF图
plt.figure(figsize=(12,8))
plt.subplot(211)
plot_acf(sample, ax=plt.gca(), lags=30)
plt.subplot(212)
plot_pacf(sample, ax=plt.gca(), lags=30)
plt.show()

对任意时间序列，当 PACF 图像呈现拖尾、且 ACF 图像呈现截尾状态时，当前时间序列适用 MA 模型，且 ACF 截尾的滞后阶数就是超参数 q 的理想值

对于 MA 模型，PACF 的拖尾可能不会很明显，这主要是因为在实际的样本数据中，PACF 可能会受到噪声的影响。不过，在理论上，MA(q) 模型的 PACF 应该在 q 阶后展现出拖尾的特性。

6.4 一般情况下如何确定 p 和 q

如果我们有一个纯随机（也称为白噪声）序列，那么它的自相关和部分自相关应该都是接近零的。这就是所谓的 “不截尾，几乎没有显著的值” 的情况。我们可以用 numpy 来生成这样一个序列。

import numpy as np
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt

np.random.seed(0)
random_series = np.random.normal(size=1000)

plt.figure(figsize=(12,8))
plt.subplot(211)
plot_acf(random_series, ax=plt.gca())
plt.subplot(212)
plot_pacf(random_series, ax=plt.gca())
plt.show()

对任意时间序列，当 ACF 图像和 PACF 图像都呈现不呈现拖尾状态时，无论图像是否截尾，时间序列都适用于 ARIMA 模型，且此时 ACF 和 PACF 图像无法帮助我们确定 p 和 q 的具体值，但能确认 p 和 q 一定都不为 0。

总的来说，ACF 和 PACF 图像可以给我们一些关于应该使用什么类型的模型（AR、MA 还是 ARIMA）以及可能的 p 和 q 值的初步想法。然而，它们不能给我们绝对的答案，因为在实际数据中可能存在一些噪声和复杂性，这就需要我们使用一些模型选择准则（如 AIC 和 BIC）来帮助我们选择最好的模型。

更准确地说，如果 ACF 拖尾，PACF 在某阶后截尾，那么应该考虑 AR 模型，PACF 截尾的阶数可能是 AR 模型的阶数。如果 ACF 在某阶后截尾，PACF 拖尾，那么应该考虑 MA 模型，ACF 截尾的阶数可能是 MA 模型的阶数。如果 ACF 和 PACF 都拖尾，那么应该考虑 ARIMA 模型。如果 ACF 和 PACF 图像都不呈现拖尾状态，那么时间序列可能是一个白噪声序列。

关于 ARIMA 模型的 p 和 q 值的选择，如果 ACF 和 PACF 都不呈现明显的拖尾或截尾，那么 p 和 q 的值可能都不为 0，这种情况下，我们可以通过 AIC 或 BIC 来选择最优的 p 和 q。

目前实践中最好的方法依然是傻瓜式尝试。在 ARIMA 模型当中，p 和 q 的值往往取值不高，一般是 [1,5] 以内的正整数，因此实践中更常用的方法是从最小值 p=1、q=1 的方式开始进行尝试，不断改变 p 和 q 的取值，直到模型通过检验或达到我们需要的精度要求。

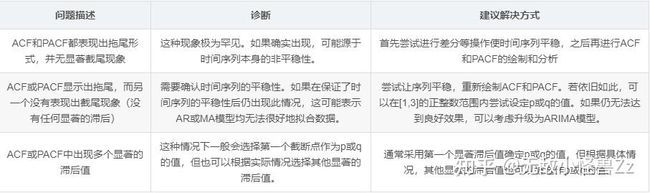
另外还有其他表现形式:

7. 评估指标

ARIMA 模型的性能通常可以使用均方误差（Mean Squared Error，MSE）、均方根误差（Root Mean Squared Error，RMSE）、平均绝对误差（Mean Absolute Error，MAE）等评估指标来 评估，当选择评估模型时，我们常使用模型评估质量指标赤池信息准则（Akaike Information Criterion，AIC） 和 贝叶斯信息准则（Bayesian Information Criterion，BIC），这两个准则都是用于模型选择的，它们考虑了模型的复杂度和拟合优度。AIC 和 BIC 越小，表示模型越好。

7.1 赤池信息准则（Akaike Information Criterion，AIC）

赤池信息准则（Akaike Information Criterion, AIC）是一个评估统计模型质量的准则，它是基于信息论的观点提出的。AIC 并非越小越好，而是应用于比较不同的模型，值越小说明模型越好。AIC 的公式如下：

$$AIC=2k-2ln(L)\text{\hspace{1em}(28)}$$

其中，k 是模型中估计参数的数量，L 是模型拟合的最大对数似然。

公式的第一部分 $2k$ 表示了模型的复杂性。参数越多（模型复杂度越高），这部分的值就越大。复杂的模型可能会导致过拟合问题，因此这部分起到了一个对模型复杂度的惩罚作用。

公式的第二部分 $-2ln(L)$表示了模型的拟合优度， $L$L 是模型的似然函数值， $ln(L)$ 就是似然函数的对数，取负数后再乘以 2。模型拟合得越好， $L$的值就越大，那么 $-2ln(L)$ 的值就越小。

因此，AIC 公式在平衡了模型的拟合优度（对数似然）和模型的复杂性（参数数量）之间的关系，寻找到既能很好地拟合数据又不会导致过拟合的模型。模型选择时，我们通常会比较不同模型的 AIC 值，选择 AIC 值最小的那个模型。

需要注意的是，AIC 只能用来比较同一数据集下的不同模型，不同数据集下计算出的 AIC 无法进行比较。此外，AIC 并不能保证选择出来的模型一定就是 “真实” 的模型，只能说在候选模型中，AIC 值最小的模型是最优的。

7.2 贝叶斯信息准则（Bayesian Information Criterion，BIC）

贝叶斯信息准则（Bayesian Information Criterion，BIC）也是用于模型选择的一种标准，它和 AIC 有很大的相似性，但在处理模型复杂性时更加严格。BIC 的公式如下：

$$BIC=ln(n)\ast k-2ln(L)\text{\hspace{1em}(29)}$$
其中，n 是观察的数据数量，k 是模型中估计参数的数量，L 是模型拟合的最大对数似然。

公式的第一部分 $ln(n)\ast k$表示了模型的复杂性。这部分与 AIC 的主要区别在于，BIC 考虑了样本数据量 n 的大小。这意味着，当数据量增加时，模型复杂性的惩罚项会增加。因此，与 AIC 相比，BIC 更倾向于选择简单的模型。

公式的第二部分 $-2ln(L)$与 AIC 公式中的这一部分相同，表示了模型的拟合优度。模型拟合得越好，L 的值就越大，那么 $-2ln(L)$的值就越小。

所以，BIC 也是在平衡模型的拟合优度和模型的复杂性，但是对于复杂模型给予了更大的惩罚。在模型选择时，我们通常会比较不同模型的 BIC 值，选择 BIC 值最小的模型。

同样的，BIC 只能用来比较同一数据集下的不同模型，不同数据集下计算出的 BIC 无法进行比较。BIC 也不能保证选择出来的模型一定就是 “真实” 的模型，只能说在候选模型中，BIC 值最小的模型是最优的。

这两个准则在实践中常常一起使用，并且可以为我们提供关于模型相对质量的有价值的信息。但是，这两个准则并不能保证我们选择的模型一定是最好的模型，还需要根据具体的业务需求和数据特性来进行选择和调整。

8. 总结

在本篇文章中，详细介绍了 ARIMA 模型的基本概念，包括 AR、I、MA 三部分的含义，以及这些概念如何组合形成 ARIMA 模型。我们也深入解释了 ARIMA 模型中的超参数 p、d 和 q 的含义，并展示了如何通过 ACF 和 PACF 图形来确定这些超参数。

最后，感谢您阅读这篇文章！如果您觉得有所收获，别忘了点赞、收藏并关注我，这是我持续创作的动力。您有任何问题或建议，都可以在评论区留言，我会尽力回答并接受您的反馈。如果您希望了解某个特定主题，也欢迎告诉我，我会乐于创作与之相关的文章。谢谢您的支持，期待与您共同成长！

期待与您在未来的学习中共同成长。