数据结构与算法——约瑟夫环

目录

一、例题引入

        # 解题思路

        #图例分析

        #代码段

        #题解小结

 二、循环链表

        分析：

        直接看代码：

 三、标记数组

        分析：

        代码：

四、递归算法 

        #沿用解释

---

一、例题引入

        设有n个人坐在圆桌周围，从第s个人开始报数，数到m时的人出列，接下来出列后的下一个人开始报数，同样是数到m的人出列，依次重复，直至所以人都出列，输出其出列的顺序。

        # 解题思路

        题解有很多种，我们这先用单链表来分析：

题目分析：本题可以先根据圆桌周围的n个人构造一个单链表，设置三个指针p、q、s，使q指向找到的第s个人对应的前驱结点，p指向第s个人对应的结点，由此进入两重for循环：第一重循环为n-1次（即要出列（输出）n-1个人，剩余一个后面再直接输出），第二重循环为寻找报数为m的人对应的结点。开始报数，使p、q依次后移（p=p->next，q=q->next）来找第m个人报数的对应的结点位置。但这会遇到一个问题：单链表的长度为n，若当s+m>n时继续查找会发生链表非法访问（NULL），所以我们必须先判断p、q的下一结点是否为空来进行处理：如果p、q两指针的下一结点都不空，即p第一遍后移还没到表尾，则p=p->next；q=q->next；若p的下一结点为NULL，即p为表尾，则让p=h->next（头结点的下一个，也是第一个结点），q=q->next；若q的下一结点为空，即指针p之前已经后移至表尾且现在已经指向头结点的下一结点，则令q=h->next；p=p->next； 此时就已经找到了报数位m的人对应的结点以及他对应的前驱结点，让r指向p（准备释放结点p），输出p->info，让p=p->next，这时能够输出第一个出列的人，但为了后面继续查找（报数）并输出下一个出列的人，还得判断p、q两指针的位置并修改它们的指向：若p->next=NULL（即p为表尾），则head->next=p；q->next=NULL；若p->next!=NULL&&q->next!=NULL（即p、q的下一结点都不为空），则q->next=p（即让q为p的前驱）；若p->next!=NULL&&q->next==NULL（即p此时已经为第二个结点，而q为表尾），则让头结点的下一个结点指向p，即head->next=p；此时p、q都找到了能够开始下一次循环的位置，释放r结点。依次重复上述操作使对应的人出列，直至链表为只剩一个结点，即为头结点的下一个结点，输出head->next->info ，结束

        #图例分析

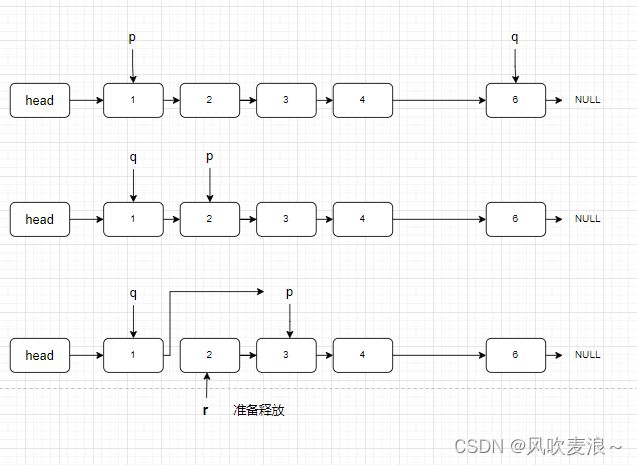
        单看思路分析可能会有点乱，让我们先根据下列图例进一步理解，我们让人数n为6，报数开始位置s为3，数数到m为2

        1.找到报数开始的位置

        2.开始报数直至m，此时找到了要出列的人对应的结点以及他的前驱结点，让p出列（输出p->info），让r指向p，准备释放，p、q仍然不为表尾，所以p=p->next；q->next=p；

        3.释放r，执行下一次出列操作。又从1开始报数，这时p为表尾，就让其指向第一个结点，即p=head->next，同时让q=q->next（q现在成了表尾），再继续报数，因为q现在为表尾，则让q=head->next；p=p->next；再一次数数到了2，令r=p；准备释放，p=p->next；q->next=p;

        4. 重复上述过程，直到n-1人出列，表中剩余最后一个结点，在循环外出列，即printf("%d",head->next->info)，结束

        #代码段

#include
#include
#include

typedef char datatype;

typedef struct _node
{
	datatype info;
	struct _node *next;
}_node;

_node* CreateLink(int n);//建立有n个结点并带头结点的链表
void joseph(int n, int s, int m);



_node* CreateLink(int n)  //建立有n个结点并带头结点的链表
{
	_node *head, *p, *q;
	if (n == 0)
	{
		return NULL;
	}

	head = (_node*)malloc(sizeof(_node));  //申请一个结点为表头
	assert(head != NULL);  //断言函数,不为空
	q = head;  //q指向头结点
	for (int i = 0; i < n; i++)
	{
		p = (_node*)malloc(sizeof(_node));
		assert(p != NULL);
		p->next = NULL;
		printf("please input element ：");
		getchar();
		scanf("%c", &p->info);
		q->next = p;
		q = p;    //q指向表尾,继续循环准备插入下一个结点
	}
	return head;  //返回头结点
}




void joseph(int n, int s, int m)//有n个人,从第s个人开始数数,报道m的人出列
{
	_node *CreateLink(int); //函数说明
	_node *p, *q, *r, *h;

	if (s > n)
	{
		return;  //找不到该结点
	}

	h = CreateLink(n);//函数调用，建立一个含有n个结点的链表
	q = h;
	for (int i = 0; i < s - 1; i++)
	{
		q = q->next;  //找到s的前驱结点
	}
	p = q->next;    //p指向s结点

	for (int i = 1; i < n; i++)   //循环n-1次,剩一个留在后面直接输出
	{
		for (int j = 1; j < m; j++)   //从当前位置开始出发找第m个结点(报数)
		{
			if (p->next != NULL&&q->next != NULL) 
			{//都为非空，即指向的下一个结点不是表尾，指针下移
				p = p->next;
				q = q->next;
			}
			else     //至少有一个是表尾
			{
				if (p->next == NULL)
				{
					p = h->next;
					q = q->next;
				}
				else  //q所指的下一个结点为表尾
				{
					q = h->next;
					p = p->next;
				}
			}
		}
		printf("%c ", p->info);//一个元素出列
		r = p;  //让r指针指向p准备释放
		if (p->next == NULL)  //p为链表尾
		{
			p = h->next;  //p指向第一个结点(即头结点的下一个)
			q->next = NULL;
		}
		else
		{
			p = p->next;//p后移一位
			if (q->next != NULL)
			{
				q->next = p;
			}
			else
			{//q为链表尾
				h->next = p;//跳过原来的第一个结点，后面释放
			}
		}
		free(r);
	}
	printf("%c", h->next->info); //输出剩余的一个人
}

int main()
{
	int n, s, m;//n个人,从s开始的第m个位置
	printf("please input n,s m：");
	scanf("%d %d %d", &n, &s, &m);
	joseph(n, s, m);

	system("pause");
	return 0;
}

        #题解小结

        基于上面的论述，我们能够用数据结构中处理单链表的方法来解决约瑟夫环的问题，通过更改p、q两指针的指向一步步的查找并出列数到m的人，但过程很繁琐，解决问题的方式不佳，所以下面我们将介绍另外几种算法，进一步优化并加深大家对该类问题的理解。

 二、循环链表

        分析：

        既然前面都能用单链表解决问题了，那对于更灵活的循环链表而言，不需要考虑单链表所谓非法访问的问题，也不需要频繁的改变指针后移的语句，只需要及时的删除出列的人对应的结点就行，那么岂不是简简单单！

        直接看代码：

#include

typedef struct _node  //重命名
{
	int data;
	struct _node* next;
}_node;

//初始化循环链表
_node* Init_List(_node *head)
{
	_node *p;
	head->data = 1;
	head->next = NULL;
	p = head;

	return p;
}

_node* push_back(_node *p, int n)//尾插
{
	for (int i = 2; i <= n; i++)
	{
		_node *r = (_node*)malloc(sizeof(_node));
		r->data = i;
		r->next = NULL;
		p->next = r;
		p = r;
	}
	return p;//返回表尾

}

int main()
{
	int n, m;//n个人,报数到m出列
	std::cin >> n >> m;

	_node *head, *p, *q, *r;
	head = q = r = (_node*)malloc(sizeof(_node));//开辟空间
	assert(head != NULL);

	p = Init_List(head);//初始化
	p= push_back(p, n);//尾插创建链表,同时构造循环链表

	p->next = head;//创建循环链表，使表尾指向表头
	p = p->next;

	while (p->next != p)//判断是否只有一个元素
	{
		for (int i = 1; i < m; i++)
		{
			q = p;//出列人的前驱结点
			p = p->next;
			r = p;//准备释放
		}
		std::cout << p->data<<" ";//出列
		q->next = p->next;
		p = p->next;//更新位置准备下一次循环
		free(r);
	}
	std::cout << p->data;
	//system("pause");
	return 0;
}

 三、标记数组

        分析：

        一开始设置一个标记数组mark[100]，让其初始化为0，0表示未出列，如若有人出列，则将其对应的位置mark[i]赋值为1，代表该人已经出列，不在需要报数，同时定义一个计数器count，判断所有人是否都已经出列，是则结束循环。

        代码：

#include

//使用mark标记数组来实现约瑟夫环问题
int main()
{
	int mark[100] = { 0 };//初始化为0代表未出列
	int m, n, count=0, i=0, j=0;  //count用来计出列人数,判断是否大于>n
	std::cin >> n >> m;//一共n个人,数到m出列（这里规定从第一人开始）

	while (count <= n)
	{
		i++;  //每个人的编号
		if (i > n)
		{
			i = 1;  //当i超出n时让其从头开始报数,即i=1
		}
		if (mark[i] == 0)//当前编号未出列，继续报数
		{
			j++;
			if (j == m)//数到m应该出列
			{
				mark[i] = 1;//出列
				std::cout << i << " ";
				j = 0;//重新报数
			}
		}
	}
	return 0;
}

四、递归算法 

        #沿用解释

        这一段比较难理解，本人水平有限，不能很好地将该递归方式的过程解释出来，所以下面我截取了他人的一部分理解，详细内容请参见博客约瑟夫环问题_小C哈哈哈的博客-CSDN博客

⭕递归方式（前提要求：学习过递归并且已经掌握递归的基本使用）— 这种方式可以不看，因为它确实较难理解不过还是要有信心学习
既然是利用递归求解，那么我们首先肯定要明确，递归函数所代表的含义，这里我暂且将递归函数命名为ysf：ysf(int N,int M,int i)：这个递归函数代表的意思为：有N个人，报到数字M时出局，求第i个人出局的编号。

比如：ysf(10,3,1)=2（假设人从0开始编号） 代表的意思就是有10个人，报到数字3时出局，第1个出局的编号为2

我们先来推：当i为1时，出局的人编号的数学公式，我们来看一个例子：假设现在总共有10个人，从0开始编号，那么就是0-9，如下图所示

现在，M=3，i=1，那么第一个出局的人就是2号，如下图，到目前为止，我们可以知道当i=1时，出局的人为：M-1

现在我们再来看另外一种情况，还是10个人，不过现在M变为11，i还是1，难道现在第一个出局的人还是M-1吗？11-1=10？，根本就不存在编号为10的这个人，此时应该出局的应该是编号为0的这个人，那怎么办呢？ 可以这样：(M-1)%N，那么不管M=3还是M=11，都可以正确得出第一个出局的人的编号。

第一个人出局的编号是完全可以通过数学公式计算而来，无需通过递归

接下来就是比较重要的了，我们还是以N=10（总人数），M=3（报的数）这个例子来说明，初始情况为：

当报数报到3，出局一个之后，变为：

此时，这些编号已经不连续了，但是3  4  5  6  7  8  9  0  1 这些数字还是紧挨着的，且下一次报数从3开始，但是，之后的报数总要考虑原编号2处空位问题

如何才能避免已经产生的空位对报数所造成的影响呢？

可以将剩下的9个连在一起的数组成一个新的环（将1、3连接），这样报数的时候就不用在意3的空位了。但是新产生的环的数字并非连续的，这就比较麻烦了。

我们需要想一种办法来解决：我们可以将组成的新的环重新编号，怎么做呢？，我们可以从刚刚出局的人的下一个人开始从0进行编号，如下图所示

但是这个时候问题又来了，怎么做才能使得在新一轮的编号中按照原规则报数得到的结果推出在旧一轮中对应的数字？，我们继续看例子，现在继续在新一轮中开始报数，那么当报数到3的时候，2号出局。此时到底怎么通过2号来推出在旧一轮中应该出局的正确编号？如何由新一轮中的2得到旧一轮中的5呢？

新一轮中的编号：（旧一轮中的编号-最大报数值M）%旧一轮中的总人数

那么，旧一轮中的编号：（新一轮的编号+最大报数值M）%旧一轮中的总人数

接下里非常重要啦！也就是说，原序列（N个人）中第二次出局的编号可以由新序列（N-1个人）第一次出局的编号通过特定的公式运算得出。

新序列（N-1个人）的编号也是从0开始的，还是这个图：

针对于这个新序列（N-1个人）第二次出局的人可以由（N-2个人）的新序列的第一次出局的人通过特定的公式推出，并且(N-1个人)这个序列第二次出局的人的编号与（N个人）这个原序列中第三次出局的人的编号是有对应关系的。

这样讲大家可能还是云里雾里的，不太明白，没有关系，接下来我们举一个例子大家就都能明白啦！，我们先来看两张图，一定要重点理解这两张图

 

我们以第一图为例子讲解：N=10，M=3

第一步：当N个人时，第一个需要出局的人为2号（编号从0开始：0-9），那么剩下的序列就是

第二步：第一步出局2号之后，剩下N-1个人，将N-1个重新编号，如下：

此时，从新一轮编号开始重新报数，报到2的时候出局，那么我们可以通过2推算出5，从而得到N个人中第二个出局的人是编号5，怎么推算呢？

旧编号=（新编号+最大报数值M）%旧一轮的人数取余（2+3）%10=5；

第三步：接下来又需要新的一轮，即N-2个人

第四步：将N-2个人重新进行编号，得到下图

第五步：N-2个人又要报数出局，而N-2个人第1个出局的人就是N-1个人时第二个出局的人，此时可以看出2号出局，如何通过2号推算出N-1个人出局时的第二个人的编号?

旧编号=（新编号+最大报数值M）%旧一轮的人数取余（2+3）%9=5；

所以N-1轮的时候第二个出局的人对应的编号是5号，而通过N-1第2个出局的人也就是5号，又可以推算出N个人时出局的第3个人

旧编号=（新编号+最大报数值M）%旧一轮的人数取余（5+3）%10=8；所以N个人时第3个出局的人的编号为8。

往后的步骤以此类推。

递归方法实现的约瑟夫环只有几行，但是理解起来却不简单，希望你们可以多花些功夫钻研，只有这样，才会成长

代码如下：

int ysf(int n, int m, int i)
{
	if (i == 1)
	{
		return (m - 1 + n) % n;//多走一圈,保证大于0
	}
	else
	{
		return ((ysf(n - 1, m, i - 1) + m) % n);
	}
}

int main()
{
	int n, m;
	std::cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		std::cout << ysf(n, m, i)<<" ";
	}

	system("pause");
	return 0;
}

原文链接：https://blog.csdn.net/xiaoxi_hahaha/article/details/113036281 

## 有关该类型的题可转至[约瑟夫环练习题](约瑟夫环练习题_leisure-pp的博客-CSDN博客)