ds图—最小生成树_学习数据结构第五章：图（图的应用）

第五章：图(图的应用)

1.最小生成树

生成树：连通图包含全部顶点的一个极小连通子图

这里需要注意的是是一个极小连通子图

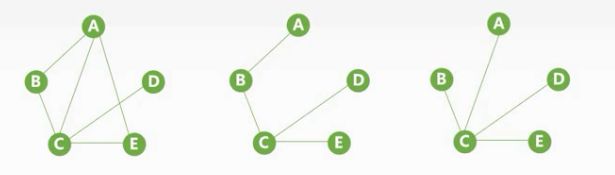
上面第一个是一个连通图，右侧两个图是它的生成树，他们包含了全部顶点且是极小连通子图，如果我们把图2中A和D链接起来他就不是一个生成树了，因为他不是极小的，如果我们把图3中的C和D中的边去掉，他也不是生成树了，因为他不是连通的。

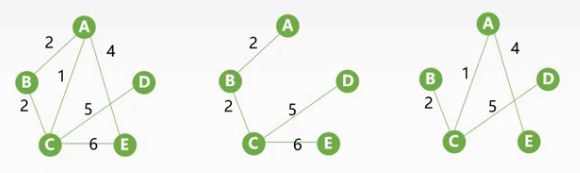
如上图，我们把图的边加上权值他就叫做网，我们找出它的两个上生成树，其中图2的所有边的权值的和为：2+2+5+6=15，图3的所有边的权值之和是：1+2+4+5=12，可以看出图3的权值之和最小，则图3就是最小生成树。

最小生成树：对于带权的无向连通图G=(V,E)，G的所有生成树当中边的权值之和最小的生成树为G的最小生成树(MST)

注意是带权的无向连通图，因为带权了才有最小的概念，只有无向连通图才有生成树

1.1性质

不一定唯一：最小生成树一定只有一种吗？

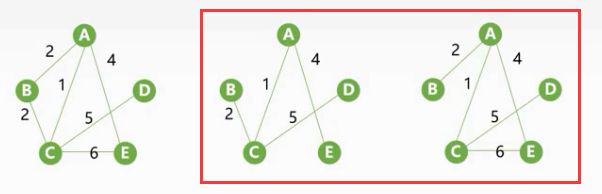
如上图中的图2和图3他们都是最小生成树，所以最下生成树不一定唯一。

这是不一定，所有也有唯一的情况，比如：

• 所有边的权重皆不相同(没有权重相同的边最小生成树必为一，可以自行尝试)
• 图中n个顶点只有n-1条边(这样的无向图【网】它的最小生成树只有一个就是他自己，所以唯一)

性质

1. 最小生成树不一定唯一,即最小生成树的树形不一定唯一。当带权无向连通图G的各边权值不等时或G只有结点数减1条边时,MST唯一

2. 最小生成树的权值是唯一的,且是最小

3. 最小生成树的边数为顶点数减1

1.2算法

我们根据贪心算法设计了如下最小生成树算法(贪心：每一步尽量做出最好的选择)

//伪代码GENRIC_MST(G){    T=NULL;    while T //未形成一棵生成树        do //找到一条最小代价边(u,v)并且加入T后不会产生回路        T=Tu(u,v);}

两种最小生成树算法：Prim、Kruskal

1.3Prim

初始化：向空的结果树T=(Vt,Et)中添加图G=(V,E)的任一顶点u0,使Vt={u0},Et为空集;

循环(直到Vt=V)：从图G中选择满足{(u,v)|u∈Vt,v∈V-Vt}且具有最小权值的边(u,v),并置Vt=VtU{v},Et=EtU{(u,v)}

{(u,v)|u∈Vt,v∈V-Vt} 相当于将已经添加到结果集中的结点和未添加进来的结点进行连接，这种方法就避免了生成的生成树出现回路

且具有最小权值的边：这个就是为了我们的最终目的啦，生成树的权值之和最小，即最小生成树

Vt=VtU{v},Et=EtU{(u,v)} 将新添加的顶点添加到结果的顶点集中，边添加到结果的边集中

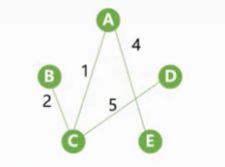
使用Prim算法生成最小生成树的过程：首先假设我们选择A作为初始顶点，然后我们从剩下的：B、C、E、D中选择一个顶点组成一条边，满足这样的边有三个：AB、AC、AE，并且我们需要选择该权值最小的那个，可以发现是AC边

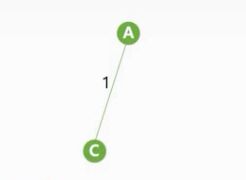
接着我们继续找，此时可以选择的顶点有三个B、E、D，可以组成的边有：AB、AE、CB、CE、CD，我们任然选择权值最小的那个CB边

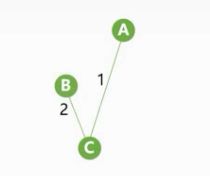
我们继续找，此时可以选择的顶点有D和E，可以组成的边有：AE、CE、CD(注意这里没有AB，因为AB边会形成通路，当然我们可选择的顶点也没有B)，任然选择权值最小的那个AE

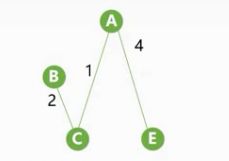
接着我们继续找，此时可以选择顶点只有D，可以组成的边只有CD

此时最小生成树构成成功，Prim算法伪代码，算法思想

void Prim(G,T){    T = 空集;//结果集    U = {w};//将w顶点加入结果的顶点集中    while((V-U)!=空集){      设(u,v)是使u∈(V-U)，且权值最小的边；         T=TuP{(u,v)};         U=Uu{V};    }}

我需要两个辅助数组将这个伪代码转成算法代码：min_weight[n],adjvex[n]

• min_weight[n] 它的数组大小是顶点的数量大小，他代表我们每次循环时，我们知道我们的边一个顶点要从结果集中选择另一个顶点要从剩下的顶点中选择，它存放了到每一个顶点：我们已经生成的顶点到我们剩下的顶点的权值最小的那条边的，数组下标是被选择的顶点的下标，例如min_weight[2]代表我们已经挑选的顶点到剩下的顶点之前权重最小的那一条边，下标2则代表结果顶点集中的顶点到剩下的顶点中下标2的顶点。
• adjvex[n] 存放该顶点由那一个顶点引入结果集中的

我们仍然使用上图作为例子，首先选A作为初始顶点，然后我们要初始化两个数组：

这里有一个无穷大的原因是A到D是没有边的，在实际算法中令这个无穷大为一个比较大的整数就可以了

接着我们同样按照上面的过程找和A顶点组成的边的权值最小的点C，接着我们此时要修改min_weight数组了

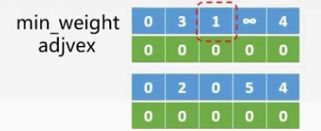
我们可以看到将3改成了2，因为在此时结果顶点集中可以存在一条从C到B的边它的权值为2比之前的AB3更小，同样修改∞为5，因为也存一条CE边，它的权值为5，因为CE的权值为6，所以4我们不需要修改，同时我们将1改成了0，因为C顶点已经被取走了，这里其中adjvex数组的值也进行修改了，我们修改adjvex[2]=0(2是c顶点的下标)，因为A顶点的下标为0，所以看不出来。

同样我们继续挑选权值最小的边BC，同样修改辅助数组此时我们已经将A、B、C三个顶点选走所数组的前三个值为0，因为B顶点是由C顶点挑选走的，所以修改adjvex=[1]=2(1代表B顶点下标，2代表C顶点下标)，由于不存在权值更小的边，所以不修改数组的值

我们继续寻找顶点，找到AE，同样我们修改此时修改min_weight=[4]=0，同时修改adjvex[4]=0,同样我们继续寻找找到CD边，我们修改min_weight[3]=0，修改adjvex[3]=2

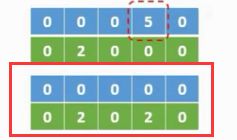
最终ming_weight数组中的值全部为0，说明所有顶点都已经被选择

代码实现，时间复杂度O(V^2) ,该算法的时间复杂度和边没有关系，所以他比较适合稠密图

void MST_Prim(Graph G){ //传入图G    int min_weight[G.vexnum];//数组大小为顶点的数量    int adjvex[G.vexnum];//数组大小为顶点的数量    for(int i=0; i        //可以看到初始顶点是下标为0的顶点，且可以看出我们的顶点这里采用的是邻接矩阵存储的        min_weight[i]=G.Edge[0][i];//存放权值        adjvex[i]=0;//初始化为0    }    int min_arc; //存放当前挑选的最小边的权重    int Min_vex; //挑选这样的一条边的另一个端点的数组下标    for(int i=1;i        min_arc=MAX;//将最小边的权重置为max，这里是为了求最小值的时候可以进行比较        for(int j=1;j            //min_weight[j]!=0不等于0代表这个顶点还没有被添加到结果集            //min_weight[j]            if(min_weight[j]!=0&&min_weight[j]                min_arc=min_weight[j];//如果小于之前的权值，修改最小的权值                min_vex=j;//同时保存最小权值结点的下标            }        }        min_weight[min_vex]=0;//表示已经该顶点已经被选择出来了        for(int j=0;j            //min_weight[j]!=0不等于0代表这个顶点还没有被添加到结果集            //G.Edge[min_arc][j]            //所以我们需要修改辅助数组的权值            if(min_weight[j]!=0&&G.Edge[min_arc][j]                min_weight[j]=G.Edge[min_arc][j];//如果加入的这条边的权值比之前的权值小则替换之前的                adjvex[j]=min_arc;//同时修改adjvex数组，因为新加入的点是通过该顶点达到的，所以修改其为对应顶点的下标            }        }    }}

1.4Kruskal

初始化：Vt=V，Et=空集，即是每个顶点构成一颗独立的树，T是一个仅含V个顶点的森林；

循环(直到T为树)：按图G的边的权值递增的顺序依次从E-Et中选择一条边，若这条边加入后不构成回路，则将其加入Et，否则舍弃。

首先将这个n个顶点放到结果集，这n个顶点构成了n棵树组成的森林，然后我们将图G的边的权值按照递增的顺序排序，接着从头挑选权值最小的那条边AC发现不构成回路，则可以加入Et中，同样我们继续挑选BC这条边不构成回路可以加入，接着是AB这条边，但是它回构成回路，不加入.......最后形成最小生成树

Kruskal主要使用了堆排序对边的权重进行排序，然后使用并查集(数组)这个数据挑选边。代码实现

代码实现，时间复杂度：O(E*logE),适用与稀疏图

typedef struct Edge{    int a,b;//改变两个端点的下标    int weight;//权重};void MST_Kruskal(Graph G,Edge *edges,int *parent){//图G、属于该图的边的集合、并查集辅助变量    heap_sort(edges);//堆排序    Initial(parent);//初始化并查集    for(int i=0;i        int a_root=Find(parent,edges[i].a);//求第一个端点所在并查集的根结点的下标        int b_root=Find(parent,edges[i].b);//求第而个端点所在并查集的根结点的下标        if(a_root!=b_root){//如果不相同            Union(parent,a_root,b_root);//并入结果集        }    }}

2.最短路径

我们之前学过无权图单源最短路径问题，那是无权图，我们找最短路径只需找出边最少的就行，但是这里我们讨论的是带权的最短路径，此时就不能只看边了。

最短路径：两个顶点之前带权路径长度最短的路径为最短路径

在带权图中，把一个顶点v到另一个顶点u所经历的权值之和称为，路径的带权路径长度

我们有两种算法：Dijkstra 、Floyd

2.1Dijkstra(迪杰斯特拉)

Dijkstra(迪杰斯特拉)：计算带权图单源最短路径。我们需要以下几个辅助数组：

• s[] 标记已经计算完成的顶点：数组中的值全部初始化为0(未计算完成)，源点下标的值初始化为1(计算完成)
• dist[] 记录从源点v0到其他各顶点当前的最短路径长度：数组中的值初始化为源点到各个顶点边的权值，即dist[i]=arcs[0][i] (我们这里源点是0，所以从第0行取值初始化，这样看源点的变化)
• path[] 记录从最短路径中顶点的前驱顶点，即path[i] 为v到vi最短路径上vi的前驱顶点(最后我们不断的求前驱系结点组成的就是一条最短路径)：数组中值的初始化，若源点v0到该顶点vi有一条有向边(无向边)，则令path[i]=0，否则path[i]=-1

实现过程：

• 初始化数组，并集合S初始化未为{0}(令源点为v0)
• 从顶点集合V-S中选出Vj，满足dist[j]=Min{dist[i],vi∈V-S}，Vj就是当前求得的最短路径的终点，并令S=S∪{j}
• 修改此时V0出发到集合V-S上任一顶点Vk的最短路径的长度：若dist[j]+arcs[j][k]则令dist[k]=dist[j]+arcs[j][k];path[k]=j;

• 重复 2、3操作n-1次，直到S中包含全部顶点

举个栗子：我们描述出下图的Dijstra的算法执行过程

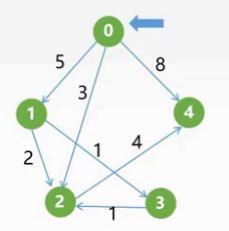
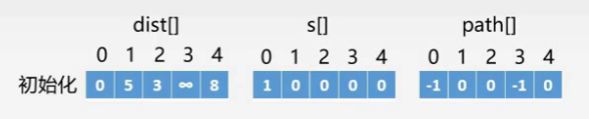
首先我们设置源点为0，接着我们初始化三个辅助数组，其中dist[]存储的是0到每一个顶点的权值因为03不存在边，所以存储∞，s[0]=1表示0这个顶点已经计算完成，path[]初始化代表如果存在顶点0到另一个顶点有一条有向边，则设置值为顶点0的下标为0，否则为-1,初始化完成，开始执行具体的执行过程

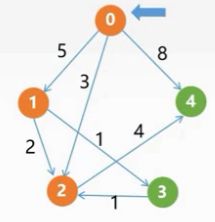
第一轮：首先我们挑选dist[]中最小的值，我们知道是3，它对应的顶点为2，所以我们挑选2这个顶点，挑选完成后我们需要修改dist[]数组，挑选2完成之后会带来新的有向边，我知道04的权值是8，但是加入2之后存在024这样的一条有向边它的权值是7，所以我们需要修改dist[4]=7，同时由于2顶点计算过了，所以我们修改s[2]=1，同时由于此时我们是通过2顶点到达的4顶点所以修改paht[4]=2

第二轮：依旧挑选最小的那个值5(0和3值对应的顶点已经计算过了)，它是1顶点对应的值，加入1顶点后带来了12和13边，对应的我们要修改dist[]的权值，这里我们只需修改从0到3的权值即可，因为从0-1-2的权值为7，而从0-2的权值为3，7>3不需要修改。同时修改s[1]=1，然后修改paht[3]=1，因为3顶点我们是通过1顶点抵达，权值为下标为1

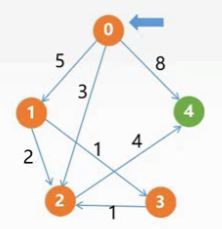
第三轮：我们挑选到3这个顶点(0、3和5值对应的顶点已经计算过了)，3这个顶点加入后会带来32这条边，所以但是2顶点已经计算完成了，所以不需要修改dist[]数组，然后我们修改s[3]=1，同样path[]数组不需要修改

image-20200620203902178

第四轮：只剩下值为7这个顶点4未被挑选了，4顶点加入后为未带来新的边，所以不修改dist[]数组，修改s[4]=1

最后遍历完成，最后我们得到s[]数组值都为1，表示所有顶点计算完成，同时dist[]数组代表顶点0到其他顶点的最短路径长度，比如5代表了0-1的最短路径长度。我们还知道path[]数组保存了最短路径经历的序列，那么我们是怎么通过path[]数组计算路径序列的呢？比如我们计算0->1路径的序列，它的长度为5，序列：首先1对应的值为0，说明它的前驱结点的下标为0，paht[0]=-1，所以结束，序列为：0->1；计算0->2路径的序列，他的长度为3，2对应的值为0，他的前驱结点为下标为0，paht[0]=-1，所以结束，序列为：0->2；计算0->3路径的序列，他的长度为6，3对应的值为1，则说明它的前驱结点的下标为1，path[1]=0，path[0]=-1，所以结束，序列为：0->1->3;......

代码实现，时间复杂度O(V^2)

注意：Dijkstra算法并不适用于含有负权值边的图

3.2Floyd(弗洛伊德算法)

Floyd(弗洛伊德算法)：计算各个顶点之间的最短路径

也就是求任意两个点之间的最短路径。这个问题这也被称为“多源最短路径”问题。

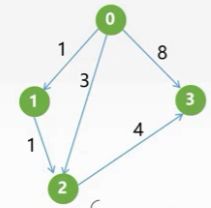
如上图，我们使用Floyd算法，进行计算各个顶点之间的最最短路径，首先进行初始化，两个顶点之间有路径的值为权值，没有路径的值为∞。

接着我们加入第一个顶点0顶点，我们随意找一个一条边比如A^(-1)[2][1],它的值为∞，表示从2顶点到1顶点没有边，然后加入0顶点后，我我们知道从2顶点到0顶点也没有边值为∞，从0顶点到1顶点有边值为1，∞+1还是∞，所以它的值A^(-1)[2][1]的值不进行更改，按照这样的方法将整个矩阵遍历一遍得到下面的矩阵：

接着我们继续加入顶点，加入顶点1，我们仍然按照上面的方法进行计算，得到A^(1)矩阵：

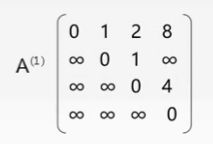
任然按照上面的方法得到A^(2)和A^(3)矩阵，其中A^(3)矩阵中的值就是各个顶点之间的最短路径

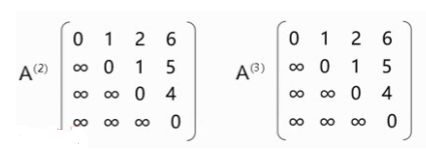
代码实现，时间复杂度：O(V^3)

整个算法的思想也可以参考整个博客 Floyd-傻子也能看懂的弗洛伊德算法(转)

3.拓扑排序

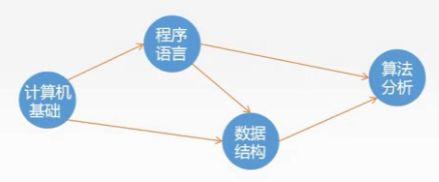
如上图，表示的就是我们只有学习了计算机基础，才能学习程序语言，然后才能学习数据结构接着才能学习算法分析，我们如果按照发生顺序对他们进行排序的话：计算机基础-程序语言-数据结构-算法分析，得到的这个序列就是拓扑排序序列。首先我们需要了解：

有向无环图：不存在环的有向图,简称DAG图。

AOV网：若用一个.AG图表示一个工程，其顶点表示活动，用有向边表示活动 vi 先于活动 vj 进行的传递关系，则将这种DAG称为顶点表示活动网络，记为AOV网。(虽然它叫网，但是它的边是没有权值的)

拓扑排序：对DAG所有顶点的一种排序，使若存在一条从顶点A到顶点B的路径，在排序中B排在A的后面

算法思想

• 1)从DAG图中选择一个没有前驱的顶点并输出

• 2)从图中删除该顶点和所有以它为起点的有向边

• 3)重复1)、2)直到当前的DAG图为空或当前图中不存在无前驱的顶点为止。后一种情况说明图中有环(则不是有向无环图)。

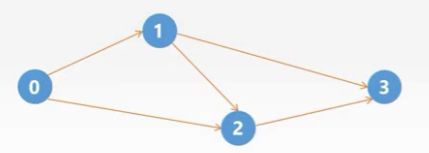
我们知道每次我们删除的是顶点入度为0的顶点，所以我们用一个辅助数组来标记当前顶点的入度，然后找出值为0的下标，我们发现是顶点0，所以我们删除顶点0，输出，并删除0顶点对应的所有的出边

然后我们要修改数组，，接着我们继续找值为0的下标，我们发现是1顶点，接着我们删除1顶点，输出，并删除1顶点对应的所有的出边

删除之后我们依旧要修改数组，，继续找值为0的下标，我们发现是2顶点，然后我们删除2顶点，输出，并删除2顶点对应的所有的出边

同样删除之后修改数组，，最后还剩3顶点，同样删除，输出。这样我们就得到这个有向无环图的拓扑排序序列：{0，1，2，3}。我们下面看一个有环的例子

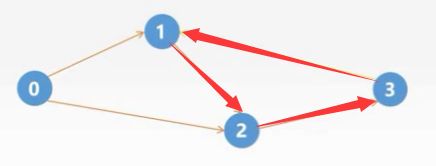
同样首先我们初始化一个数组，然后找到值为0的顶点0，接着删除顶点0，并输出，并删除顶点0对应的出边

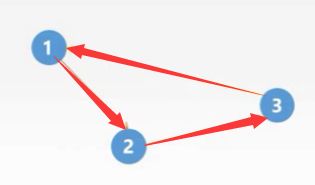
然后修改数组：，然后我们发现没有顶点的入度为0，即为算法描述中第三个步骤当前图中不存在无前驱的顶点，此时图为有环图。

即：算法结束时没有访问所有顶点，则存在以剩下顶点组成的环。

然后我们继续看一个例子：

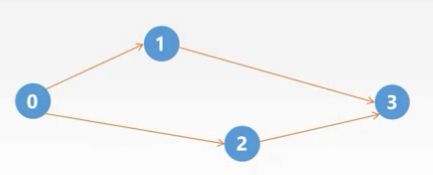
首先我们初始化一个数组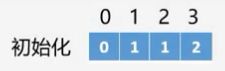：，然后找出值为0的顶点，找到了0顶点，然后删除0顶点，输出，并删除0顶点对应的出边

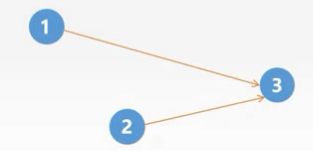
接着修改数组：，此时我们发现有两个顶点的入度都为0，此时选择那个一个顶点先开始都可以，那么到最后我们发现此有向无环图有两种拓扑排序的序列：{0，1，2，3} 或 {0，2，1，3}

即：拓扑排序的结果不一定唯一

代码实现，时间复杂度：O(V+E)

拓扑排序的特点：

• 若邻接矩阵为三角矩阵，则存在拓扑排序；反之不一定成立

例如：，上三角矩阵，它如果是某一个有向图的邻接矩阵的话，则对应在该有向图中一定满足如下条件：Vi->Vj中的i，那么在该有向图中一定不存在环状结构，那么一定存在拓扑排序的排序序列，下三角矩阵同理。

反之不一定成立因为比如：0->2，2->1，我们也可以得到一个拓扑排序序列，但是这个图对应的邻接矩阵不是一个三角矩阵。

4.关键路径

上面我们讲解了拓扑排序的AVO网这里我们讲另外一种网AOE网，使用每一个有向边表示活动，权值常常代表一个活动所需要的金钱或者时间开销等等，顶点表示的是事件

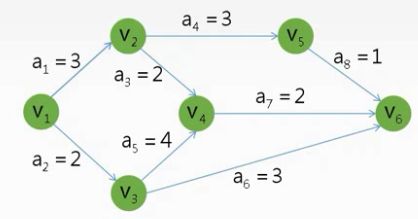
AOE网：在有向带权图中，以顶点表示事件，以有向边表示活动，以边上权值表示完成该活动的开销(如完成活动所需要的时间)，则称这种有向图为用边表示活动的网络，简称AOE网

上面讲的AOV网是没有权重的

AOE网有以下特点：

• 它始终只有一个顶点是完全没有入边的，我们称为源点，如上图的V1
• 它始终只有一个顶点是完全没有出边的，我们称为汇点，如上图的V6

顶点与入边的关系：如上图V4顶点和入边a3、a5，边代表活动，点代表事件，只有a3和a5的活动都结束才能开始V4顶点的事件(上图V2和V3事件同时开始)

顶点与出边的关系：如上图V4顶点和出边a7，表示只有V4顶点的事件完成后才能进行a7活动

关键路径：从原点到汇点最大路径长度的路径(权重和最大的路径)称为关键路径，关键路径上的活动为 关键活动

关键路径为什么关键？我们知道例如一个工程，关键路径上的关键活动直接决定的工程的完成事件，我们知道了关键路径，我们就可以进行优化关键路径，提升工程的完成效率等等

4.1关键路径的计算

1、事件Vk的最早发生时间Ve(k)

我们可以看一下图中的顶点V4，从V1到顶点V4(我们默认V1耗时为0)，有两条路径：V1->V2->V4；V1->V3->V4；路径1耗时3+2=5，路径2耗时2+4=6；那么事件V4最早发生时间是？这时可能有人会说5小时，其实答案是6，因为事件V4的发生必须满足a3和a5同时完成。

Ve(源点)=0; Ve(k)=Max{Ve(j)+Weight(Vj,Vk)}

Weight(Vj,Vk)：顶点Vj到当前顶入边的权值

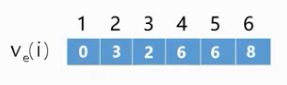
上图各个顶点的最早发生时间

2、事件Vk的最迟发生时间Vl(k)

解释：我们在不推迟整个工程的完成时间的情况下，每个事件它最迟可以什么时间开始

计算方式其实和最早发生事件是相反的，我们从汇点向源点。

Vl(汇点)=Ve(汇点);//令汇点的最迟发生时间等于汇点的最早发生时间，如果我们汇点的最迟发生时间大于汇点的最早发生时间那么我们就等于推迟了工程的结束时间，所以只能相等

Vl(j)=Min{Vl(k)-Weight(Vj,Vk)}  我们计算最早发生时间使用了入边，这里我们使用出边向源点进行逆推。

例如：Vl(2)的最迟发生时间，我们可以使用Ve(4)-a3=4和Ve(5)-a4=3进行比较找出最小值

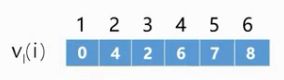上图各个顶点的最迟发生时间

上图各个顶点的最迟发发生时间

3、活动ai的最早开始时间e(i)

我们知道每一个事件所需事件为0，那么每一个活动的最早开始时间就是整个活动的弧的弧头这个事件的最早开始时间即

若存在表示活动ai，则e(i)=Ve(k)

我们只需找到每个事件的最早开始事件，然后对应每个活动即可找到每个活动的最早开始时间

4、活动ai的最迟开始时间l(j)

若存在表示活动ai，则l(i)=Vl(j)-Weight(Vk,Vj)

我们只需找到每个事件的最迟开始时间，然后依次计算每个活动的最迟开始时间：例如a1的最迟开始时间等于Vl2-a1的权重=4-3=1

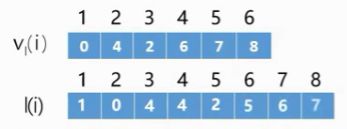
5、活动ai的差额d(i)=l(i)-e(i)

最迟发生时间减去最早发生时间等与活动的差额，我们先计算出每个活动的最迟发生时间和最早发生时间然后做个减法

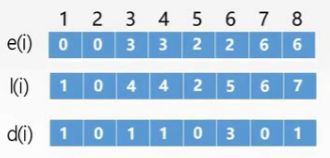
我们通过活动的差额可以找到关键活动，其中值为零的就是关键活动，值为零说明此活动的最迟发生时间和最早发生时间相同，对于这些活动我们不能早开始也不能晚开始，都会影响整个工程的时间，这些活动当然就是工程的关键活动，我们利用这些关键活动可以组成关键路径：V1->V3->V4->V6，我们如果想优化整个工程就要优化整个工程的关键路径上的关键活动。

注意：缩短关键活动时间可以加快整个工程，但缩短到一定大小时关键路径会发生改变

例子：

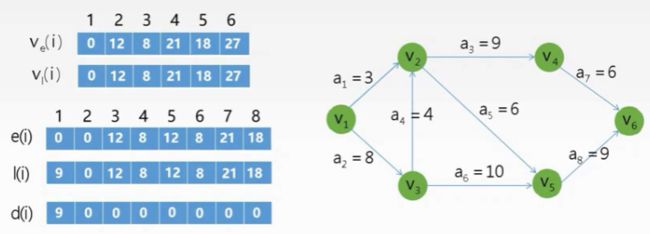
在该AOE网中有以下关键活动路径：{a2，a4，a3，a7}；{a2，a4，a5，a8}；{a2,a6,a8}

由此可以看出不是所有的AOE网只有一条关键路径，其实AOE网可能有多条关键路径。那么就出现了一个问题，如果我们想要缩减整个工程的时间的话，如果只缩减一条关键路径上的关键活动就可以吗？答案是可能可以，如果该关键活动包含在所有的关键活动中。就如上图，如果我们缩减a2即可达到缩减整个工程的目的。但是如果我们缩减a5，不能改变整个工程的时间。

即：当网中关键路径不唯一时,只有加快的关键活动或关键活动组合包括在所有的关键路径上才能缩短工期。