力扣总结之回溯算法+深度优先+广度优先
目录
回溯算法基本思想
回溯和递归的区别
深度优先算法基本思想
回溯算法和深度优先算法的区别是?
例题
1. 有效的括号组合
2.全排列
3.全排列Ⅱ
回溯算法基本思想
回溯算法是系统地搜索问题的解的方法。
某个问题的所有可能解的称为问题的解空间,若解空间是有限的,则可将解空间映射成树结构。
任何解空间可以映射成树结构的问题,都可以使用回溯法。
回溯法是能够在树结构里搜索到通往特定终点的一条或者多条特定路径。
回溯算法的基本思想是:从一条路往前走,能进则进,不能进则退回来,换-条路再试,从而搜索到抵达特定终点的一条或者多 条特定路径。
值得注意,回溯法以深度优先搜索的方式搜索解空间,诅在搜索过程中用剪枝函数避免无效搜索。
回溯和递归的区别
为了描述问题的某一状态,必须用到该状态的上一状态,而描述上一状态,又必须用到上一状态的上一状态……这种用自已来定义自己的方法,称为递归定义。形式如 f(n) = n*f(n-1), if n=0,f(n)=1.
从问题的某一种可能出发, 搜索从这种情况出发所能达到的所有可能, 当这一条路走到” 尽头 “的时候, 再倒回出发点, 从另一个可能出发, 继续搜索. 这种不断” 回溯 “寻找解的方法, 称作” 回溯法 “。
深度优先算法基本思想
深度度优先搜索的能够在图结构里搜索到通往特定终点的一条或者多条特定路径。每条路深入到不能再深入,并且每条个点只访问一次;属于盲目搜索,最糟糕的情况算法时间复杂度为O(n!)。
回溯算法和深度优先算法的区别是?
可以浅显地认为回溯=深度优先+剪枝函数
但是两者却又存在不同,就是深度优先算法适用于所有的图但是回溯只适合于树结构
例题
1. 有效的括号组合
题目描述
数字
n代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。示例:
输入:n = 3 输出:["((()))","(()())","(())()","()(())","()()()"]
解题思路
对于这题,首先我们知道他需要我们找到所有的可能;并且这里是需要得到所有的组合,那试想一下我们学数据结构的时候是不是学过一种结构----树,可以列出我们所有的可能性,那么,我们就可以使用回溯的方法进行求解了
public class Solution {
// 做减法
public List generateParenthesis(int n) {
List res = new ArrayList<>();
// 特判
if (n == 0) {
return res;
}
// 执行深度优先遍历,搜索可能的结果
dfs("", n, n, res);
return res;
}
/**
* @param curStr 当前递归得到的结果
* @param left 左括号还有几个可以使用
* @param right 右括号还有几个可以使用
* @param res 结果集
*/
private void dfs(String curStr, int left, int right, List res) {
// 因为每一次尝试,都使用新的字符串变量,所以无需回溯
// 在递归终止的时候,直接把它添加到结果集即可,注意与「力扣」第 46 题、第 39 题区分
if (left == 0 && right == 0) {
res.add(curStr);
return;
}
// 剪枝(如图,左括号可以使用的个数严格大于右括号可以使用的个数,才剪枝,注意这个细节)
if (left > right) {
return;
}
if (left > 0) {
dfs(curStr + "(", left - 1, right, res);
}
if (right > 0) {
dfs(curStr + ")", left, right - 1, res);
}
}
}
2.全排列
题目描述
给定一个不含重复数字的数组
nums,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
思路描述
在这里,全排列应该怎么求解?
首先我们要想到对于这个类型的题目,很适合使用回溯来解决,回溯的思想在于搜索到所有解并且本题使用树的结构就可以表示清楚我们想要的数据的所有可能性,当然回溯是最可靠的,然后我们本题应该怎么求解?
[1,2,3]--> [1]+[2,3]
[1,2,3]-->[2]+[1,3]
[1,2,3]-->[3]+[1,2]
然后我们就可以通过画树的方法来解决了,如下图所示:
然后有了这些之后我们就需要知道需要什么变量?
我们分析实现过程:
①我们从根节点出发
②找到一条路径,判断当前节点是否访问,如果没有被访问就加入,被访问就返回到上一个节点
那么显而易见的需要的变量有:
①判断当前节点有没有被访问 boolean []used
②存放所有结果的集合 List
然后我们继续分析还需要哪些变量?
①当前路径上的集合 List path=new ArrayList<>();
②当前所在的树的位置 int depth
代码展示
class Solution {
public List> permute(int[] nums) {
Solution solution=new Solution();
int len=nums.length;
List> res=new ArrayList<>();
//如果当前数组不存在的话,就返回空的数组
if(len==0){
return res;
}
//首先我们需要一个数组取表示当前数据有没有被读取
boolean []used=new boolean[len];
//然后我们需要一个数组来存储当前的路径,这里不写泛型是会自动补充泛型
List path=new ArrayList<>();
solution.dfs(nums,len,res,0,path,used);
return res;
}
public void dfs(int[] nums,int len,List> res,int depth,List path, boolean[] used) {
if (depth == len ){
res.add(new ArrayList(path));
return ;
}
for(int i=0;i 当然也可以使用不回溯的方法
import java.util.ArrayList;
import java.util.List;
public class Solution {
public List> permute(int[] nums) {
// 首先是特判
int len = nums.length;
// 使用一个动态数组保存所有可能的全排列
List> res = new ArrayList<>();
if (len == 0) {
return res;
}
boolean[] used = new boolean[len];
List path = new ArrayList<>();
dfs(nums, len, 0, path, used, res);
return res;
}
private void dfs(int[] nums, int len, int depth,
List path, boolean[] used,
List> res) {
if (depth == len) {
// 3、不用拷贝,因为每一层传递下来的 path 变量都是新建的
res.add(path);
return;
}
for (int i = 0; i < len; i++) {
if (!used[i]) {
// 1、每一次尝试都创建新的变量表示当前的"状态"
List newPath = new ArrayList<>(path);
newPath.add(nums[i]);
boolean[] newUsed = new boolean[len];
System.arraycopy(used, 0, newUsed, 0, len);
newUsed[i] = true;
dfs(nums, len, depth + 1, newPath, newUsed, res);
// 2、无需回溯
}
}
}
}
最后,为什么不使用广度优先?
①广度优先是一层一层的找,但是深度是一条路走到黑,那么是不是我们使用深度的时候只需要为一个变量设置有没有使用,但是对于广度需要为一层!
②如果使用广度优先遍历就得使用队列,然后编写结点类。队列中需要存储每一步的状态信息,需要存储的数据很大,真正能用到的很少 。
③使用深度优先遍历,直接使用了系统栈,系统栈帮助我们保存了每一个结点的状态信息。我们不用编写结点类,不必手动编写栈完成深度优先遍历。
3.全排列Ⅱ
题目描述
给定一个可包含重复数字的序列
nums,按任意顺序 返回所有不重复的全排列。
思路描述
本题相对于全排列那题来说,多了一个去重?那么我们怎么解决?我们可以想到回溯法的组成为深度优先+剪枝,那么我们是不是可以把不需要的地方也就是多余的地方进行剪枝,最后就可以得到我们想要的结果了!
那么怎么剪枝?
下面是详细的操作过程:
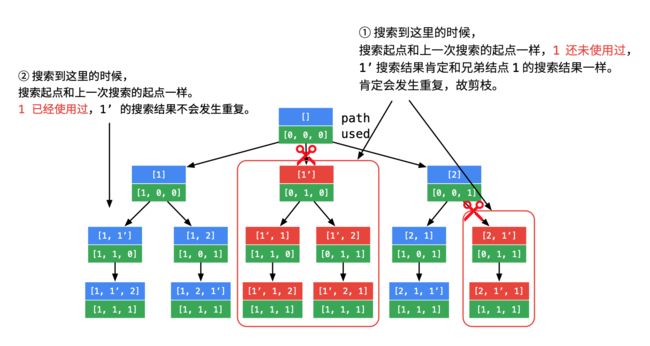
对比图中标注 ① 和 ② 的地方。相同点是:这一次搜索的起点和上一次搜索的起点一样。不同点是:
标注 ① 的地方上一次搜索的相同的数刚刚被撤销;
标注 ② 的地方上一次搜索的相同的数刚刚被使用。
产生重复结点的地方,正是图中标注了「剪刀」,且被绿色框框住的地方。
大家也可以把第 2 个 1 加上 ' ,即 [1, 1', 2] 去想象这个搜索的过程。只要遇到起点一样,就有可能产生重复。这里还有一个很细节的地方:
在图中 ② 处,搜索的数也和上一次一样,但是上一次的 1 还在使用中;
在图中 ① 处,搜索的数也和上一次一样,但是上一次的 1 刚刚被撤销,正是因为刚被撤销,下面的搜索中还会使用到,因此会产生重复,剪掉的就应该是这样的分支。
那么就需要在上一题的基础上加上如下代码:
if(i > 0 && nums[i] == nums[i - 1] && !used[i - 1]){
continue;
}代码展示
public class Solution {
public List> permuteUnique(int[] nums) {
int len = nums.length;
List> res = new ArrayList<>();
if (len == 0) {
return res;
}
// 排序(升序或者降序都可以),排序是剪枝的前提
Arrays.sort(nums);
boolean[] used = new boolean[len];
// 使用 Deque 是 Java 官方 Stack 类的建议
Deque path = new ArrayDeque<>(len);
dfs(nums, len, 0, used, path, res);
return res;
}
private void dfs(int[] nums, int len, int depth, boolean[] used, Deque path, List> res) {
if (depth == len) {
res.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < len; ++i) {
if (used[i]) {
continue;
}
// 剪枝条件:i > 0 是为了保证 nums[i - 1] 有意义
// 写 !used[i - 1] 是因为 nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
continue;
}
path.addLast(nums[i]);
used[i] = true;
dfs(nums, len, depth + 1, used, path, res);
// 回溯部分的代码,和 dfs 之前的代码是对称的
used[i] = false;
path.removeLast();
}
}
}