- Java升级版的学生成长管理系统
学生成长管理系统升级版需求为了学生管理系统书写一个登录、注册、忘记密码的功能。只有用户登录成功之后,才能进入学生管理系统中进行增删查改操作。分析登录界面System.out.println("欢迎来到学生成长管理系统");System.out.println("请选择操作1登录2注册3忘记密码");用户类属性:用户名、密码、身份证号码、手机号码注册功能用户名需求满足以下要求:验证要求:用户名唯一用
- 风险管理:从评估到分析的完整指南
""背景简介在面对日益复杂化的网络安全挑战时,有效的风险管理成为了企业和组织不可或缺的一部分。本文基于提供的章节内容,将探讨风险管理的核心过程,包括风险评估和风险分析的步骤,以及如何选择合适的方法论来应对不同的风险场景。风险管理过程的持续监控风险管理并非一成不变,它需要一个持续的监控过程来确保控制措施的有效性。章节中提到,监控(Monitor)是风险管理过程中的一个持续步骤,它负责观察控制措施,并
- 区块链技术核心组件及应用架构的全面解析
区块链技术是一套融合密码学、分布式系统与经济激励的复合型技术体系,以下是其核心组件及应用架构的全面解析:一、区块链核心技术栈1.分布式账本技术(DLT)核心原理:多节点共同维护不可篡改的数据链数据结构:哈希指针哈希指针区块N区块N+1区块N+2关键创新:默克尔树(MerkleTree)实现高效数据验证2.密码学保障技术算法示例应用场景非对称加密ECC/secp256k1,RSA数字签名(设备身份认
- 利用TCP协议,创建一个多人聊天室
在下Z.
tcp/ip网络协议网络
项目名称利用TCP协议,做一个带有登录,注册的无界面,控制版的多人聊天室。知识点循环,判断,集合,IO,多线程,网络编程准备内容在当前模块下新建txt文件,在文件中保存正确的用户名和密码zhangsan=123lisi=1234wangwu=12345页面搭建客户端连接服务器后,显示如下服务器已经连接成功==============欢迎来到小周聊天室================1登录2注册请输
- 介绍6款密码暴力破解工具
网安导师小李
程序员网络安全编程web安全网络安全tcp/ipphppythonjava
暴力破解就是通过不断穷举可能的密码,直至密码验证成功,暴力破解分为密码爆破和密码喷洒,密码爆破就是不断的去尝试不同的密码,密码喷洒就是通过已知密码不断去尝试账号。下面介绍6款常见的暴力破解工具。01hydraHydra(九头蛇)是THC组织开发的,是一款非常流行的密码破解工具,可以对多种服务的账号和密码进行爆破,包括Web登录、数据库、SSH、FTP等服务,支持Linux、Windows、Mac平
- 2024年最全kali无线渗透之用wps加密模式可破解wpa模式的密码12_kali wps,网络安全开发究竟该如何学习
2401_84558314
程序员wpsweb安全学习
一、网安学习成长路线图网安所有方向的技术点做的整理,形成各个领域的知识点汇总,它的用处就在于,你可以按照上面的知识点去找对应的学习资源,保证自己学得较为全面。二、网安视频合集观看零基础学习视频,看视频学习是最快捷也是最有效果的方式,跟着视频中老师的思路,从基础到深入,还是很容易入门的。三、精品网安学习书籍当我学到一定基础,有自己的理解能力的时候,会去阅读一些前辈整理的书籍或者手写的笔记资料,这些笔
- 《密码爆破漏洞详解》——黑客必修的入门操作( 建议收藏 )
2401_84573531
2024年程序员学习python
隔壁老张:“狗剩啊,隔壁xx村的王姐家的女娃好漂亮,我想盗她qq啊,你帮我把”狗剩:“我不会呀”村里大妈:“那个狗剩啊,盗个qq号都不会,他妈妈还好意思说他是学网络安全当黑客的”密码爆破漏洞详解密码爆破介绍密码爆破使用场景密码爆破利用思路防范密码爆破密码的复杂性密码加密登录逻辑验证码登录次数限制密码爆破介绍密码爆破又叫暴力猜解,简单来说就是将密码逐个尝试,直到找出真正的密码为止,本质上是利用了穷举
- Kali系统MSF模块暴力破解MySQL弱口令漏洞
一、实验环境1.攻击方:攻击环境使用KALI系统(使用虚拟机搭建)的Metasploit模块,msfconsole是metasploit中的一个工具,它集成了很多漏洞的利用的脚本,并且使用起来很简单的网络安全工具。这里要特别强调:被攻击的环境必须开启mysql远程登陆服务,通常MySQL开启的端口号是3306,故而一般情况下要求被攻击的服务器开启了3306端口号。2.被攻击MySQL环境:Wind
- 网络安全/Web安全/渗透测试入门/信息收集
&Sinnt&
网络安全web安全网络安全
网络安全/Web安全/渗透测试入门/信息收集本篇文章主要讲解如何进行信息收集,列举了在信息收集中常见的工具和手段。原文地址:sinblog一,whois查询WHOIS查询是一种查找域名注册信息的工具或服务。WHOIS是一个协议,允许用户查询某个域名或IP地址的域名、注册信息以及其他相关互联网的详细数据。WHOIS数据库由多个注册商提供和注册机构维护,公开提供域名注册人的信息。自己购买一个域名,配置
- 三生原理在三个关键历史断层中实现中西科学传统的创造性弥合?
葫三生
三生学派算法数学建模人工智能机器学习量子计算
AI辅助创作:三生原理通过重构科学史的叙事逻辑,在三个关键历史断层中实现了中西科学传统的创造性弥合,其核心突破如下:一、科学方法论断层:实验主义与直觉理性的融合西方实验传统的局限欧洲科学革命依赖形式逻辑与实验验证(如伽利略斜面实验),但面临复杂系统建模的瓶颈。三生原理将《周易》“阴阳动态平衡”转化为参数化递归模型(如素性塔的三级筛除结构),在密码学应用中实现效率提升40%,证明东方直觉
- 恶搞锁屏软件
梦遇苏喂
软件工程安全
这是一个打包好的锁屏程序适用于恶搞同学老师密码在软件里使用此软件使电脑发生任何问题与作者无关!!!!!下载链接-百度https://pan.baidu.com/s/16DiF-Fv8us-lBSZgh6-W-A?pwd=awer下载链接-迅雷https://pan.xunlei.com/s/VOUZN96XqftxLLdlNjbtnmX-A1?pwd=fm4a
- 网络安全概论——身份认证
陇西李氏
web安全网络安全网络安全服务器
一、身份证明身份证明可分为以下两大类身份验证——“你是否是你所声称的你?”身份识别——“我是否知道你是谁?”身份证明系统设计的三要素:安全设备的系统强度用户的可接受性系统的成本实现身份证明的基本途径所知:个人所知道的或所掌握的知识,如密码、口令等。所有:个人所具有的东西,如身份证、护照、信用卡、钥匙等。个人特征:如指纹、笔迹、声纹、视网膜、虹膜、DNA及个人一些动作方面的特征等。二、口令认证系统口
- Rust 注释
froginwe11
开发语言
Rust注释引言Rust编程语言以其内存安全、并发支持和高性能等特点在软件开发领域获得了广泛的关注。在Rust编程中,注释是一种非常重要的元素,它不仅可以帮助程序员理解代码,还可以提高代码的可维护性和可读性。本文将详细介绍Rust中的注释类型、语法及其应用场景。一、Rust注释类型Rust中的注释主要分为两种类型:单行注释和多行注释。1.单行注释单行注释用于对代码的某一小部分进行简要说明。其语法格
- 攻防对抗的工作原理和架构
hao_wujing
安全
大家读完觉得有帮助记得关注和点赞!!!**攻防对抗(CyberKillChainDefense)**是网络安全领域的动态博弈过程,攻击方通过**入侵链**突破防御,防御方则构建**纵深的检测响应体系**进行拦截反制。其本质是**攻击成本与防御效能的持续对抗升级**。以下从工作原理到架构的深度解析:---###一、攻防对抗核心工作原理####**攻击链(CyberKillChain)vs防御链(De
- 网络安全相关专业总结(非常详细)零基础入门到精通,收藏这一篇就够了
网络安全工程师教学
兼职副业黑客技术网络安全web安全安全人工智能网络运维
一、网络工程专业专业内涵网络工程是指按计划进行的以工程化的思想、方式、方法,设计、研发和解决网络系统问题的工程,一般指计算机网络系统的开发与构建。该专业培养具备计算机科学与技术学科理论基础,掌握网络技术领域专业知识和基本技能,在计算机、网络及人工智能领域的工程实践和应用方面受到良好训练,具有深厚通信背景、可持续发展、能力较强的高水平工程技术人才。学生可在计算机软硬件系统、互联网、移动互联网及新一代
- 自学黑客(网络安全),一般人我劝你还是算了吧
网络安全工程师教学
兼职副业网络安全黑客技术web安全安全网络人工智能学习
我是一名8年半的网安工程师“老司机”,要给准备入坑的同学泼盆冷水了,网络安全真的不是一般人能学的。有人会问“你一个8年的网安老司机,为什么还给大家泼冷水”?好多人说:网安基础很简单,是个人稍微认真点都能懂,给网安打上了简单、易懂的标签。然后上来就是一波言论浮夸的输出,把一些很基础很浅显的技术点拆解出来,让小白快速上手,误导新手,让他们以为网络安全就这么回事儿,可一到真正实操,哦豁,啥也不会。这导致
- 【Python】python_jwt
宅男很神经
python开发语言
1.1传统会话(Session)机制的黄金时代与黄昏在Web应用的黎明时期,身份验证的范式几乎完全由**基于服务器端会话(Session-BasedAuthentication)**的机制所主导。这是一个直观且在单体应用时代极其有效的模型,其工作流程如同一场精密的双人舞:凭证交换与“储物柜钥匙”的签发:用户在登录页面输入用户名和密码。这些凭证被发送到服务器。服务器验证其有效性后,会在自己的“储物间
- 卵生兄弟网络工作原理和架构
hao_wujing
安全
大家读完觉得有帮助记得关注和点赞!!!以下从网络安全角度解析**卵生兄弟网络**的深度技术架构与工作原理。该概念通常指**具有冗余唤醒和协同攻击能力的模块化恶意网络**(如APT组织所用),或**防御端的双生活动目录/蜜罐系统**。我们将从攻击与防御两个维度展开:---###一、攻击视角:恶意「卵生兄弟网络」架构(APT高级威胁)####**核心设计目标**-**隐蔽持久化**:主模块被清除时,备
- 【网络安全基础】第七章---无线网络安全
薄荷椰果抹茶
信息安全与网络安全web安全网络安全
仅供参考文章目录一、无线安全二、移动设备安全三、IEEE802.11四、IEEE802.11i五、习题训练一、无线安全严重威胁无线网络安全的关键因素:信道、移动性、资源、可访问性无线网络环境由三部分组成,为攻击提供了切入点:无线客户(手机等)、无线接入点(Wifi热点等)、传递无线电波无线网络安全威胁:无线安全措施:安全无线传输、安全的无线接入点、安全的无线网络无线网络安全主要通过加密和认证来实现
- 【网络安全基础】第八章---电子邮件安全
薄荷椰果抹茶
信息安全与网络安全安全web安全网络
仅供参考文章目录一、电子邮件协议二、邮件格式2.1RFC53222.2MIME2.3S/MIME(重点)三、域名系统(DNS)四、域名密钥识别邮件(DKIM)一、电子邮件协议传输邮件时使用两种协议:1)简单的邮件传输协议SMTP——把消息通过互联网从源移动到目的地2)邮件访问协议——用于在邮件服务器之间传输信息,两个最常使用:POP3(邮局协议):允许客户端从邮件服务器上下载邮件IMAP(网络邮件
- 马尔可夫链:随机过程的记忆法则与演化密码
大千AI助手
人工智能Python#OTHERpython人工智能马尔科夫链MC算法随机过程
本文由「大千AI助手」原创发布,专注用真话讲AI,回归技术本质。拒绝神话或妖魔化。搜索「大千AI助手」关注我,一起撕掉过度包装,学习真实的AI技术!一、核心定义:无记忆的随机演化马尔可夫链(MarkovChain)是一种具有马尔可夫性质的离散随机过程,其核心特征是:未来状态仅取决于当前状态,与历史路径无关数学表述:[P(Xt+1=xt+1∣Xt=xt,Xt−1=xt−1,…,X0=x0)=P(Xt
- 备份远程主机上mysql,mongodb上数据,在docker容器中导入
酒千殇
数据备份dockermongodbmysql数据备份ubuntu
将远程机器中的mysql,mongodb数据备份到Ubuntu20.04中前提:一定要明确数据库的版本。已知:远程机器ip,mysql账号,密码。说明:以下命令均在Ubuntu20.04中执行查看远程mysql的版本:用mysqlworkbench连接上远程数据库。点击Query菜单,在空白框输入selectversion();在点击菜单栏中第二个闪电符号,执行这条命令。就可以在下面的输出中看到m
- Excel 如何让某些符合特定条件的数据自动变色,以作警示?
冰糖心书房
Excelexcel
回答这个问题我们得用Excel中一个极为实用的功能——条件格式(ConditionalFormatting)。条件格式能让单元格根据其自身的值或与其他单元格的关系,自动改变外观(如背景色、字体颜色、图标等)。这就像给数据装上了一个“自动警报系统”,让关键信息和异常数据在第一时间“跳”出来。一、条件格式的核心位置在Excel菜单栏的开始(Home)选项卡中,你会找到一个非常显眼的条件格式(Condi
- vscode remote-ssh 拓展免密访问 linux虚拟机
前置步骤,在linux安装好ssh并且win可以使用密码登录linuxsudoaptinstallopenssh-server-y在win上检查密钥是否存在检查公钥和私钥cat~/.ssh/id_rsa.pubcat~/.ssh/id_rsa如果不存在,重新生成ssh-keygen-trsa-b4096重新执行cat~/.ssh/id_rsa.pub将公钥的内容粘贴到linux下~/.ssh/au
- 实验五-Flask的简易登录系统
亚力山大抵
pythonflaskpython后端
一、实验目的和任务1.掌握Flask框架的基本使用方法2.理解Web应用的会话管理机制3.实现用户认证系统的基本功能4.学习模板继承和表单处理技术要求:请将思考题的答案写在实验报告中二、实验内容1.基础环境搭建:创建项目目录结构、安装必要依赖包2.核心功能实现:用户注册(用户名、密码)、用户登录验证、会话状态管理、用户退出功能3.前端界面开发:基础模板设计、注册/登录表单实现4.系统测试验证:注册
- 0代码改动实现应用运行时数据库密码无损轮转
阿里-于怀
oracle数据库nacos
作者:柳遵飞一.敏感数据的安全风险在应用程序中,访问数据库几乎是必须的,是实现业务功能的基础普遍场景,应用程序访问数据库,需要设置数据库的地址,端口,账号及密码。密码的安全性非常重要,业界密码泄漏导致资损的事件时有发生,根据相关统计,单次泄漏事件的发生平均导致488万美元(约合人民币3542万元),每条泄漏的数据记录平均导致169美元(约合人民币1226元),除了直观的资金损失外,对企业的形象和舆
- 解读国密非对称加密算法SM2
云水木石
详解国密算法数据安全
本文先介绍非对称加密算法,然后聊一聊椭圆曲线密码算法(EllipticCurveCryptography,ECC),最后才是本文的主题国密非对称加密算法SM2。因为我的数学知识有限,对于算法涉及的一些复杂的理论知识,也是不懂,所以本文不会涉及理论,仅仅从编程的角度解读一下SM2。在进行国密算法开发的这段时间,我主要参考的书籍是《深入浅出HTTPS:从原理到实战》,微信读书上也有电子版,如果你也是进
- 2025数字经济新政策解码:这五个黄金赛道,正在改写财富分配规则
数据与人工智能律师
人工智能大数据网络算法区块链
首席数据官高鹏律师团队创作,AI辅助一、政策东风下的财富重构:当免税清单变成“造富密码”2025年的春天,数字经济领域的政策“礼包”如同春雷炸响。从跨境电商的“阳光化新政”到智慧农业的“技术普惠”,从汽车零部件的“出海红利”到工业升级的“智能改造”,再到文旅餐饮的“消费重构”,五大行业正在经历一场财富分配的底层变革。这不是普通的政策调整,而是国家战略级的资源再分配——免税+补贴的组合拳,正在为先行
- 极客开发者如何打造下一个DeepSeek:从技术颠覆到生态构建的深度思考
山顶望月川
人工智能
DeepSeek的成功首先源于其技术范式的根本性突破...1.1架构创新的三大支柱DeepSeek的技术优势建立在三大创新基础之上...1.2极客开发者的技术启示对于有志打造下一个DeepSeek的极客开发者...二、生态战略:从封闭花园到开源雨林DeepSeek的第二个成功密码在于其开放生态战略...2.1开源生态的双重价值DeepSeek的开源策略创造了双重价值...2.2构建开发者生态的关键
- reveiw of test --welcome www.1maitao.com
从0到1的技术进阶
数据结构算法出版网络生活
--welcomewww.1maitao.comA数学的复习:1.最好能在7月前开始,如果你基础不是很好,又想在数学多拿分的话。2.课本很重要,08和09的题已经充分说明了基础的重要性,最好在5——6月把两册高数书及例题过两遍,有个宏观的把握,拿到题,就知道是在考什么。3.参考书的选择:个人觉得李永乐那本复习全书更注重基础,更贴近这2年的考研风格。全书中线性代数那100多页讲得超好。4.复习进度:
- java的(PO,VO,TO,BO,DAO,POJO)
Cb123456
VOTOBOPOJODAO
转:
http://www.cnblogs.com/yxnchinahlj/archive/2012/02/24/2366110.html
-------------------------------------------------------------------
O/R Mapping 是 Object Relational Mapping(对象关系映
- spring ioc原理(看完后大家可以自己写一个spring)
aijuans
spring
最近,买了本Spring入门书:spring In Action 。大致浏览了下感觉还不错。就是入门了点。Manning的书还是不错的,我虽然不像哪些只看Manning书的人那样专注于Manning,但怀着崇敬 的心情和激情通览了一遍。又一次接受了IOC 、DI、AOP等Spring核心概念。 先就IOC和DI谈一点我的看法。IO
- MyEclipse 2014中Customize Persperctive设置无效的解决方法
Kai_Ge
MyEclipse2014
高高兴兴下载个MyEclipse2014,发现工具条上多了个手机开发的按钮,心生不爽就想弄掉他!
结果发现Customize Persperctive失效!!
有说更新下就好了,可是国内Myeclipse访问不了,何谈更新...
so~这里提供了更新后的一下jar包,给大家使用!
1、将9个jar复制到myeclipse安装目录\plugins中
2、删除和这9个jar同包名但是版本号较
- SpringMvc上传
120153216
springMVC
@RequestMapping(value = WebUrlConstant.UPLOADFILE)
@ResponseBody
public Map<String, Object> uploadFile(HttpServletRequest request,HttpServletResponse httpresponse) {
try {
//
- Javascript----HTML DOM 事件
何必如此
JavaScripthtmlWeb
HTML DOM 事件允许Javascript在HTML文档元素中注册不同事件处理程序。
事件通常与函数结合使用,函数不会在事件发生前被执行!
注:DOM: 指明使用的 DOM 属性级别。
1.鼠标事件
属性
- 动态绑定和删除onclick事件
357029540
JavaScriptjquery
因为对JQUERY和JS的动态绑定事件的不熟悉,今天花了好久的时间才把动态绑定和删除onclick事件搞定!现在分享下我的过程。
在我的查询页面,我将我的onclick事件绑定到了tr标签上同时传入当前行(this值)参数,这样可以在点击行上的任意地方时可以选中checkbox,但是在我的某一列上也有一个onclick事件是用于下载附件的,当
- HttpClient|HttpClient请求详解
7454103
apache应用服务器网络协议网络应用Security
HttpClient 是 Apache Jakarta Common 下的子项目,可以用来提供高效的、最新的、功能丰富的支持 HTTP 协议的客户端编程工具包,并且它支持 HTTP 协议最新的版本和建议。本文首先介绍 HTTPClient,然后根据作者实际工作经验给出了一些常见问题的解决方法。HTTP 协议可能是现在 Internet 上使用得最多、最重要的协议了,越来越多的 Java 应用程序需
- 递归 逐层统计树形结构数据
darkranger
数据结构
将集合递归获取树形结构:
/**
*
* 递归获取数据
* @param alist:所有分类
* @param subjname:对应统计的项目名称
* @param pk:对应项目主键
* @param reportList: 最后统计的结果集
* @param count:项目级别
*/
public void getReportVO(Arr
- 访问WEB-INF下使用frameset标签页面出错的原因
aijuans
struts2
<frameset rows="61,*,24" cols="*" framespacing="0" frameborder="no" border="0">
- MAVEN常用命令
avords
Maven库:
http://repo2.maven.org/maven2/
Maven依赖查询:
http://mvnrepository.com/
Maven常用命令: 1. 创建Maven的普通java项目: mvn archetype:create -DgroupId=packageName
- PHP如果自带一个小型的web服务器就好了
houxinyou
apache应用服务器WebPHP脚本
最近单位用PHP做网站,感觉PHP挺好的,不过有一些地方不太习惯,比如,环境搭建。PHP本身就是一个网站后台脚本,但用PHP做程序时还要下载apache,配置起来也不太很方便,虽然有好多配置好的apache+php+mysq的环境,但用起来总是心里不太舒服,因为我要的只是一个开发环境,如果是真实的运行环境,下个apahe也无所谓,但只是一个开发环境,总有一种杀鸡用牛刀的感觉。如果php自己的程序中
- NoSQL数据库之Redis数据库管理(list类型)
bijian1013
redis数据库NoSQL
3.list类型及操作
List是一个链表结构,主要功能是push、pop、获取一个范围的所有值等等,操作key理解为链表的名字。Redis的list类型其实就是一个每个子元素都是string类型的双向链表。我们可以通过push、pop操作从链表的头部或者尾部添加删除元素,这样list既可以作为栈,又可以作为队列。
&nbs
- 谁在用Hadoop?
bingyingao
hadoop数据挖掘公司应用场景
Hadoop技术的应用已经十分广泛了,而我是最近才开始对它有所了解,它在大数据领域的出色表现也让我产生了兴趣。浏览了他的官网,其中有一个页面专门介绍目前世界上有哪些公司在用Hadoop,这些公司涵盖各行各业,不乏一些大公司如alibaba,ebay,amazon,google,facebook,adobe等,主要用于日志分析、数据挖掘、机器学习、构建索引、业务报表等场景,这更加激发了学习它的热情。
- 【Spark七十六】Spark计算结果存到MySQL
bit1129
mysql
package spark.examples.db
import java.sql.{PreparedStatement, Connection, DriverManager}
import com.mysql.jdbc.Driver
import org.apache.spark.{SparkContext, SparkConf}
object SparkMySQLInteg
- Scala: JVM上的函数编程
bookjovi
scalaerlanghaskell
说Scala是JVM上的函数编程一点也不为过,Scala把面向对象和函数型编程这两种主流编程范式结合了起来,对于熟悉各种编程范式的人而言Scala并没有带来太多革新的编程思想,scala主要的有点在于Java庞大的package优势,这样也就弥补了JVM平台上函数型编程的缺失,MS家.net上已经有了F#,JVM怎么能不跟上呢?
对本人而言
- jar打成exe
bro_feng
java jar exe
今天要把jar包打成exe,jsmooth和exe4j都用了。
遇见几个问题。记录一下。
两个软件都很好使,网上都有图片教程,都挺不错。
首先肯定是要用自己的jre的,不然不能通用,其次别忘了把需要的lib放到classPath中。
困扰我很久的一个问题是,我自己打包成功后,在一个同事的没有装jdk的电脑上运行,就是不行,报错jvm.dll为无效的windows映像,如截图
最后发现
- 读《研磨设计模式》-代码笔记-策略模式-Strategy
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/*
策略模式定义了一系列的算法,并将每一个算法封装起来,而且使它们还可以相互替换。策略模式让算法独立于使用它的客户而独立变化
简单理解:
1、将不同的策略提炼出一个共同接口。这是容易的,因为不同的策略,只是算法不同,需要传递的参数
- cmd命令值cvfM命令
chenyu19891124
cmd
cmd命令还真是强大啊。今天发现jar -cvfM aa.rar @aaalist 就这行命令可以根据aaalist取出相应的文件
例如:
在d:\workspace\prpall\test.java 有这样一个文件,现在想要将这个文件打成一个包。运行如下命令即可比如在d:\wor
- OpenJWeb(1.8) Java Web应用快速开发平台
comsci
java框架Web项目管理企业应用
OpenJWeb(1.8) Java Web应用快速开发平台的作者是我们技术联盟的成员,他最近推出了新版本的快速应用开发平台 OpenJWeb(1.8),我帮他做做宣传
OpenJWeb快速开发平台以快速开发为核心,整合先进的java 开源框架,本着自主开发+应用集成相结合的原则,旨在为政府、企事业单位、软件公司等平台用户提供一个架构透
- Python 报错:IndentationError: unexpected indent
daizj
pythontab空格缩进
IndentationError: unexpected indent 是缩进的问题,也有可能是tab和空格混用啦
Python开发者有意让违反了缩进规则的程序不能通过编译,以此来强制程序员养成良好的编程习惯。并且在Python语言里,缩进而非花括号或者某种关键字,被用于表示语句块的开始和退出。增加缩进表示语句块的开
- HttpClient 超时设置
dongwei_6688
httpclient
HttpClient中的超时设置包含两个部分:
1. 建立连接超时,是指在httpclient客户端和服务器端建立连接过程中允许的最大等待时间
2. 读取数据超时,是指在建立连接后,等待读取服务器端的响应数据时允许的最大等待时间
在HttpClient 4.x中如下设置:
HttpClient httpclient = new DefaultHttpC
- 小鱼与波浪
dcj3sjt126com
一条小鱼游出水面看蓝天,偶然间遇到了波浪。 小鱼便与波浪在海面上游戏,随着波浪上下起伏、汹涌前进。 小鱼在波浪里兴奋得大叫:“你每天都过着这么刺激的生活吗?简直太棒了。” 波浪说:“岂只每天过这样的生活,几乎每一刻都这么刺激!还有更刺激的,要有潮汐变化,或者狂风暴雨,那才是兴奋得心脏都会跳出来。” 小鱼说:“真希望我也能变成一个波浪,每天随着风雨、潮汐流动,不知道有多么好!” 很快,小鱼
- Error Code: 1175 You are using safe update mode and you tried to update a table
dcj3sjt126com
mysql
快速高效用:SET SQL_SAFE_UPDATES = 0;下面的就不要看了!
今日用MySQL Workbench进行数据库的管理更新时,执行一个更新的语句碰到以下错误提示:
Error Code: 1175
You are using safe update mode and you tried to update a table without a WHERE that
- 枚举类型详细介绍及方法定义
gaomysion
enumjavaee
转发
http://developer.51cto.com/art/201107/275031.htm
枚举其实就是一种类型,跟int, char 这种差不多,就是定义变量时限制输入的,你只能够赋enum里面规定的值。建议大家可以看看,这两篇文章,《java枚举类型入门》和《C++的中的结构体和枚举》,供大家参考。
枚举类型是JDK5.0的新特征。Sun引进了一个全新的关键字enum
- Merge Sorted Array
hcx2013
array
Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array.
Note:You may assume that nums1 has enough space (size that is
- Expression Language 3.0新特性
jinnianshilongnian
el 3.0
Expression Language 3.0表达式语言规范最终版从2013-4-29发布到现在已经非常久的时间了;目前如Tomcat 8、Jetty 9、GlasshFish 4已经支持EL 3.0。新特性包括:如字符串拼接操作符、赋值、分号操作符、对象方法调用、Lambda表达式、静态字段/方法调用、构造器调用、Java8集合操作。目前Glassfish 4/Jetty实现最好,对大多数新特性
- 超越算法来看待个性化推荐
liyonghui160com
超越算法来看待个性化推荐
一提到个性化推荐,大家一般会想到协同过滤、文本相似等推荐算法,或是更高阶的模型推荐算法,百度的张栋说过,推荐40%取决于UI、30%取决于数据、20%取决于背景知识,虽然本人不是很认同这种比例,但推荐系统中,推荐算法起的作用起的作用是非常有限的。
就像任何
- 写给Javascript初学者的小小建议
pda158
JavaScript
一般初学JavaScript的时候最头痛的就是浏览器兼容问题。在Firefox下面好好的代码放到IE就不能显示了,又或者是在IE能正常显示的代码在firefox又报错了。 如果你正初学JavaScript并有着一样的处境的话建议你:初学JavaScript的时候无视DOM和BOM的兼容性,将更多的时间花在 了解语言本身(ECMAScript)。只在特定浏览器编写代码(Chrome/Fi
- Java 枚举
ShihLei
javaenum枚举
注:文章内容大量借鉴使用网上的资料,可惜没有记录参考地址,只能再传对作者说声抱歉并表示感谢!
一 基础 1)语法
枚举类型只能有私有构造器(这样做可以保证客户代码没有办法新建一个enum的实例)
枚举实例必须最先定义
2)特性
&nb
- Java SE 6 HotSpot虚拟机的垃圾回收机制
uuhorse
javaHotSpotGC垃圾回收VM
官方资料,关于Java SE 6 HotSpot虚拟机的garbage Collection,非常全,英文。
http://www.oracle.com/technetwork/java/javase/gc-tuning-6-140523.html
Java SE 6 HotSpot[tm] Virtual Machine Garbage Collection Tuning
&
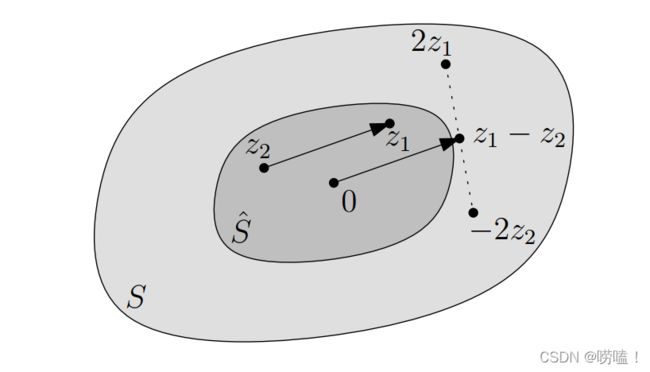
![]() 和可测量的集合
和可测量的集合![]() ,如果满足
,如果满足![]() ,那么必定存在
,那么必定存在![]() ,满足
,满足![]() 。如下图所示:
。如下图所示:![]() ,则存在重合点。具体分析思路如下:
,则存在重合点。具体分析思路如下:![]() 的格基,让x遍历所有格点
的格基,让x遍历所有格点![]() ,如下集合构成n维空间
,如下集合构成n维空间![]() 的一部分:
的一部分:![]()
![]()
![]()
![]()
![]()
![]() 以及
以及![]()
![]()
![]() ,保证
,保证![]() 。用z代表
。用z代表![]() 中的点,所以z+x一定包含在
中的点,所以z+x一定包含在![]() ,z+y包含在
,z+y包含在![]() 。所以
。所以![]() 也包含在
也包含在![]() 中。定理证明完毕。
中。定理证明完毕。![]() 时,
时,![]() ;因为是个凸体,当
;因为是个凸体,当![]() 且
且![]() ,不难推出
,不难推出![]() 。中心对称和凸体的前提条件,去掉任何一个,闵可夫斯基凸体定理就会不成立。
。中心对称和凸体的前提条件,去掉任何一个,闵可夫斯基凸体定理就会不成立。![]() 和中心对称凸集
和中心对称凸集![]() ,若
,若![]() ,则S包含非零格点。
,则S包含非零格点。![]() 。所以
。所以![]() 。根据BLICHFELD理论,一定存在两个点
。根据BLICHFELD理论,一定存在两个点![]() ,满足
,满足![]() 且不是原点。根据定义,
且不是原点。根据定义,![]() ,又因为S是中心对称的,所以
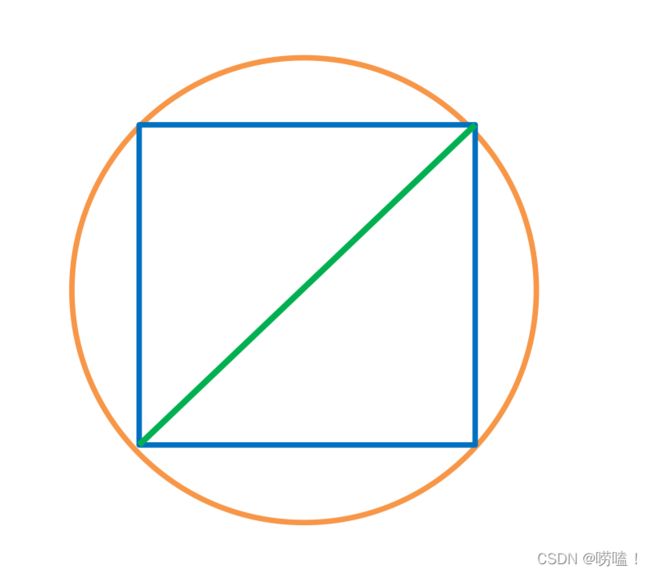
,又因为S是中心对称的,所以![]() 。另外由于S是凸体,
。另外由于S是凸体,![]() 也在空间S中。如下图所示:
也在空间S中。如下图所示:![]()
![]() 的立方体。如下图:
的立方体。如下图:![]() 。证明完毕。
。证明完毕。![]() ,其最短向量长度满足如下:
,其最短向量长度满足如下:![]()
![]() 内包含非零格点,根据以上分析可得:
内包含非零格点,根据以上分析可得:![]() 。整理此式子不难得出
。整理此式子不难得出![]() 的上界。
的上界。![]() 不含任何非零格点+闵可夫斯基凸体定理。
不含任何非零格点+闵可夫斯基凸体定理。![]() 看起来可能有些奇怪,实际上有它本身的意义:能够与空间维度联系起来。例如,将格
看起来可能有些奇怪,实际上有它本身的意义:能够与空间维度联系起来。例如,将格![]() 看成原格
看成原格![]() 扩大c倍产生。所以易得
扩大c倍产生。所以易得![]() 。另一方面,在n维度上
。另一方面,在n维度上![]() ,等式右边正如我们所理解的那样扩大c倍。由此得出结论,任意秩为n,行列式为1的格,最短向量的上界为
,等式右边正如我们所理解的那样扩大c倍。由此得出结论,任意秩为n,行列式为1的格,最短向量的上界为![]() 。
。![]() ,考虑一组格基
,考虑一组格基![]() ,此格的行列式为1,依据闵可夫斯基第一定理可得上界为
,此格的行列式为1,依据闵可夫斯基第一定理可得上界为![]() ,然而实际最短向量为
,然而实际最短向量为![]() 。实际上,已经有研究将
。实际上,已经有研究将![]() 的上界缩小到
的上界缩小到![]() 。此处讨论的二维可以拓展到多维。
。此处讨论的二维可以拓展到多维。![]() 。加强版的连续最小值问题可以由闵可夫斯基第二定理说明,以下研究的不只是
。加强版的连续最小值问题可以由闵可夫斯基第二定理说明,以下研究的不只是![]() ,考虑的是
,考虑的是![]() 的几何平均数。
的几何平均数。![]() ,其连续最小值最小值满足:
,其连续最小值最小值满足:![]()
![]() 为连续最小值代表的向量,也就是
为连续最小值代表的向量,也就是![]() 。令
。令![]() 代表对应的Gram_Schmidt正交化结果。引入一个椭球体,轴为
代表对应的Gram_Schmidt正交化结果。引入一个椭球体,轴为![]() 所在的直线,长度为
所在的直线,长度为![]() 。可得如下椭球体内部空间(不包含边界):
。可得如下椭球体内部空间(不包含边界):![]()
![]() 向量在椭圆的边界,
向量在椭圆的边界,![]() 向量在椭圆的外部,如下图:
向量在椭圆的外部,如下图:,让
使得k是对应的最大值,且满足如下不等式:
是k+1个线性独立的向量,且要求它们的长度就都小于
,显然是互相矛盾的。所以可得
。
。
![]()
![]()