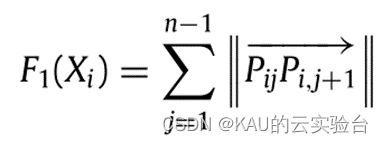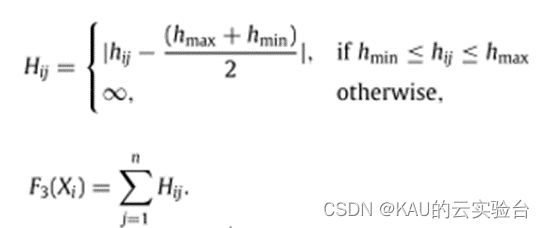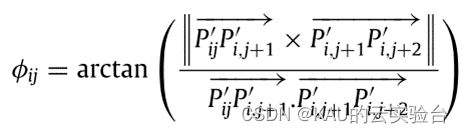UAV | 多算法在多场景下的无人机路径规划(Matlab)

近年来，无人机(unmanned aerial vehicle，UAV)由于其灵活度高、机动性强、安全风险系数小、成本低等特点，被广泛应用于搜索巡逻、侦察监视、抢险救灾、物流配送、电力巡检、农业灌溉等军用或民用任务。路径规划是无人机执行任务的关键，也是自主无人机在工程应用上的主要挑战。

现有的无人机路径规划算法主要分为经典算法和元启发式算法，经典算法包括：A*算法、快速搜索随机数RRT等，但这些算法在面对复杂环境时搜索效率较低，收敛迟缓。而元启发式算法即在启发式算法基础上改进的一种智能优化算法，路径优化问题是典型的NP-hard问题，其常带有复杂约束，一般的求解器很难找到精确解，但PSO、GA、GWO等智能优化算法能够有效求解复杂的组合优化问题，因而在无人机路径规划的研究中已经得到广泛的应用。

因此，本文将元启发式算法应用于几个不同复杂程度的地形模型，同时，考虑到一些智能优化算法容易陷入局部最优解，因此本文也引入作者的一些原创改进算法以进一步提升其全局搜索性能。

00 文章目录

1 UAV路径规划问题建模

2 智能优化算法、原创改进算法原理

3 代码目录

4 仿真实验

5 源码获取

01 UAV路径规划问题建模

在复杂的地形中，无人机按照路径规划结果从起始点飞向目标点。在飞行过程中，无人机可能面临地形障碍、火力威胁、雷达扫描区域等障碍物，同时有燃料消耗，最大爬升和最大转弯能力等约束，为保证UAV的安全协调飞行，路径规划算法需要得到连接起点和终点的最佳路径。

假设无人机保持预先给定的飞行速度。这样，路径规划问题就被简化为一个静态的折线规划问题。考虑无人机的运行要求，因此通过计算航程长度成本、飞行高度成本、威胁成本和平滑成本，定义无人机路径规划的成本函数，其数学表示如下：

其中，Xi是决策变量，为n个航站点(x,y,z)的列表，bk为各成本函数的权重，Fk为第k个成本函数。下面具体介绍一下这4个成本函数。本篇中的成本函数的参考文献为[1]。

1.1 航程长度成本

无人机的飞行路线的长度应尽可能短，以保存无人机的燃料消耗，其通过多个段的总和来计算。将两个节点之间的欧几里得距离作为每个段的长度，然后计算特定路径P的路径长度成本如下：

1.2 威胁成本

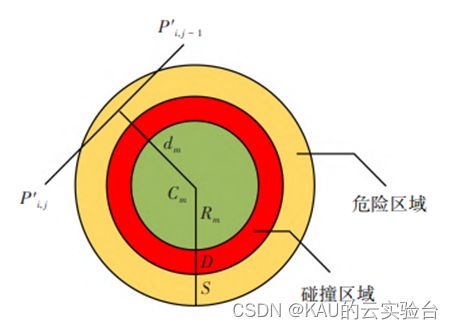
除了路径长度最优之外，路径规划中的路径还必须要确保无人机的安全运行，可能会遇到被称为威胁区域的禁飞区（例如雷达探测、防空装备攻击或天气威胁等）。考虑到威胁建模的复杂性和获取真实数据的困难性，本文对威胁环境进行了抽象化处理，将威胁区域抽象为一个半径为定值的圆柱体，威胁区域的作用半径等同于圆柱体的半径，设置威胁区域的目的是为了满足无人机的飞行环境，让无人机成功避开威胁区域以完成飞行任务。其图像如下：

设M为所有存在威胁的障碍物集合；障碍物模型为圆柱体，其投影的圆心为Cm；Rm为障碍物的半径；D为无人机的直径，相邻两个路径节点与原点的垂直距离为dm，S表示障碍物的危险区域，该值取决于无人机的定位精度与飞行环境。如果无人机处于静态环境中且 GPS 信号良好，那么 S 的值可能是几十米；如果环境中存在移动的物体或GPS信号差，那么S的值将超过百米。对于一个路径，其威胁成本计算式为：

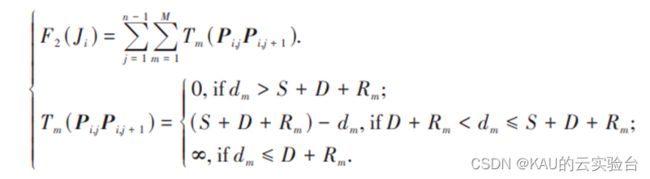
当无人机在危险区域以外的地方飞行时，不存在碰撞的风险，其威胁为零；而当无人机经过危险区域时，dm越小威胁越大；当无人机途经碰撞区域时，无人机会碰撞坠毁，此时设定该路径的威胁赋值为无穷。

1.3高度成本

UAV飞行高度通常由最小高度hmin和最大高度hmax约束，例如，对于测量和搜索时，需要由相机以特定分辨率和视角收集视觉数据。如图所示，

图源文献[1]

则高度成本计算如下：

可以看出，高度成本将保持平均高度并惩罚超出范围的值。

1.4 平滑成本

无人机的飞行角度控制参数主要包括水平转向角和垂直俯仰角，这两个参数变量必须满足无人机的实际角度约束，否则轨迹规划模型无法生成可行的飞行路径。如图所示，

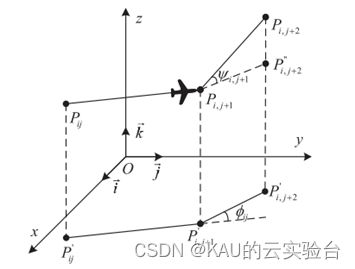
图源文献[1]

水平转向角φij是投影在水平面Oxy上的两个连续路径段之间的角度，水平转向角计算为：

垂直俯仰角ψij是投影在竖轴上的两个连续路径段之间的角度，则垂直俯仰角计算为：

则平滑成本计算如下：

式中，a1和a2分别为水平转向角和垂直俯仰角的惩罚系数。

1.5 环境建模

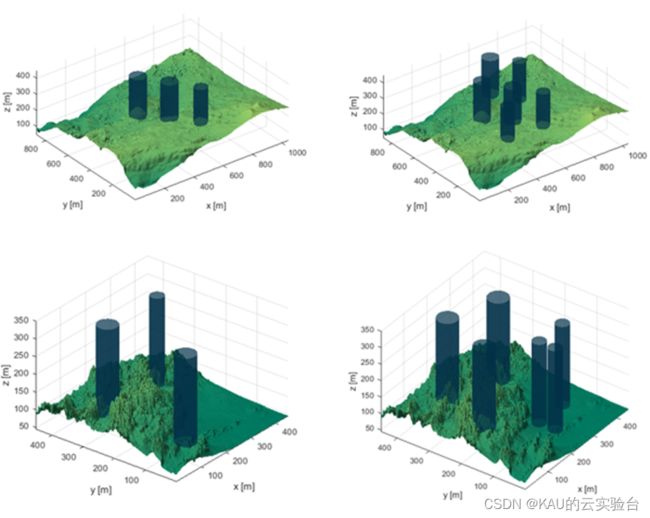
本文使用真实的数字高程模型DEM地图进行作为无人机路径规划问题中的环境。选择了一个澳大利亚圣诞岛的DEM，以及另一个具有不同地形结构的数据地图。对其增添不同的威胁物以对不同复杂度的地形进行模拟，最终共生成4个地形以供路径规划，地形环境如下：

1.6 解的编码

文献[1]中创新从地方之一就是他用的是球形矢量坐标而不是我们通常的直角坐标，球形坐标可以表示如下：

他用径向距离r，极角θ，方位角φ来表示位置，若三维直角坐标是(x,y,z)，那么球坐标就是(r,θ,φ)。这种编码方式的优点在于，若将优化算法中的解的种群按r,θ,φ编码，那么其可以描述出某个点到下一个点的运动轨迹，并且也可以完美使其运动轨迹满足于平滑成本中的转向角和俯仰角的要求，与随机产生n个直角坐标相比，这种方式产生的解质量更高、更容易产生可行解，当固定速度飞行时，可以固定其r。

举一个容易理解的例子：

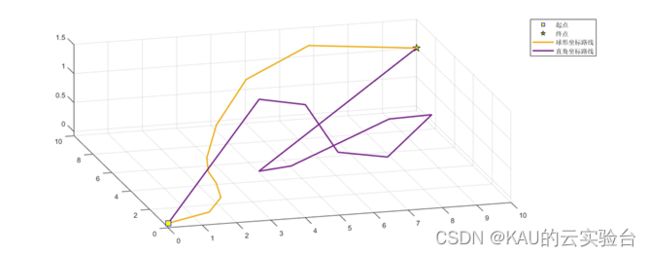
若采用直角坐标系进行初始化种群，则是下面的紫色线，其xyz都是随机产生，因此下一个节点虽然可以在空间的任何位置，但节点间没有关联，容易产生不满足于约束的解，而球形坐标能够基于上一个点进行运动，获得可行解的几率更高。

球形坐标与直角坐标的转换关系如下：

其中，ρ就是径向距离r，ψ就是极角θ，φ就是方位角φ

02智能优化算法、原创改进算法原理

本文使用了灰狼、鲸鱼、粒子群等共6种智能优化算法，并引入了作者的原创改进算法

03 代码目录

代码仅有MATLAB版本，包含乱码解决方案，若运行出现问题可联系我。

部分代码如下：

可以看到，作者已基本整理的和函数测试的代码格式一致，非常方便大家进行修改。

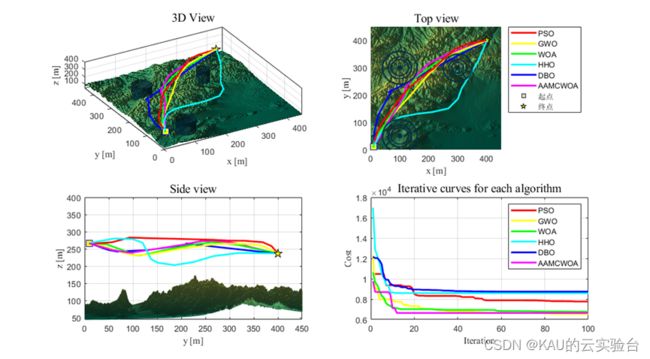
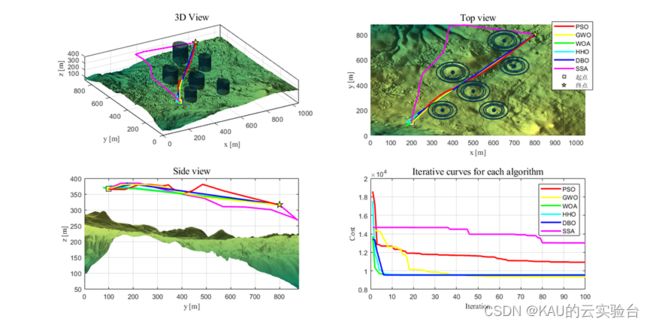
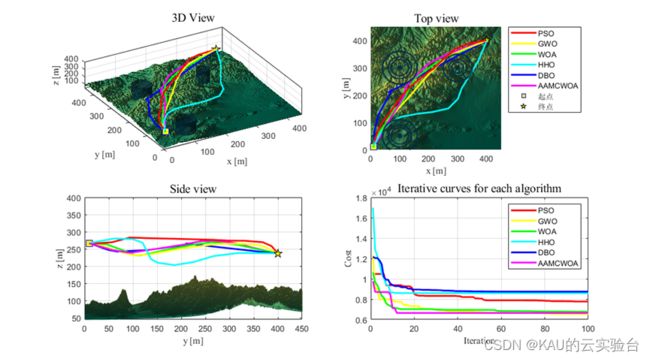
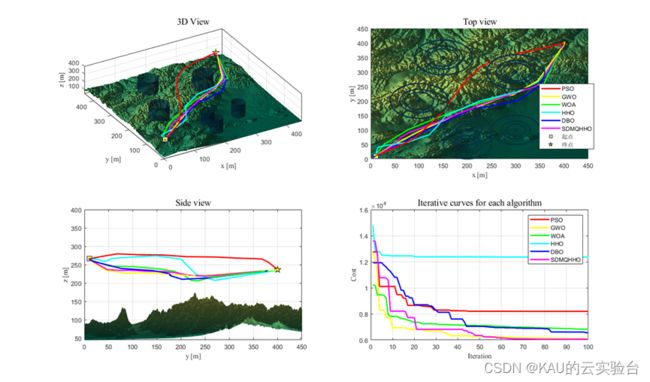
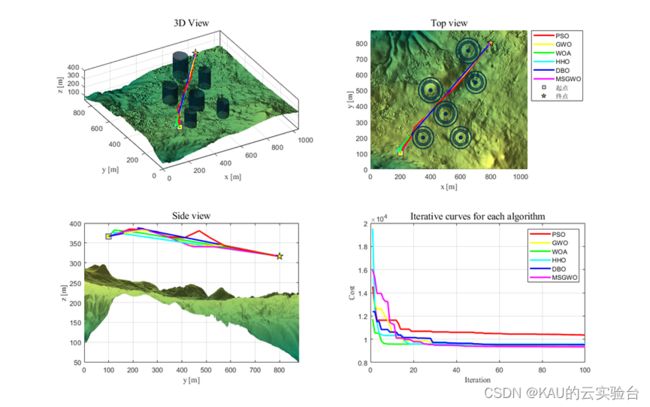
04 仿真实验

其中，绘图的结果和我在程序中设定的各成本函数的权值有关

另外，作者也引入了在往期文章中的原创改进算法，部分结果如下：

05 源码获取

1.作者的此版本的代码基础即是文献[1]中的开源代码，这份代码对UAV的编程学习有很大的帮助

大家可以 搜索该文献获取其代码 或 GZH（KAU的云实验台）后台回复：UAV2 获取其 github地址。

2.本文代码：

GZH（KAU的云实验台）后台回复：UAVB

3.包含作者原创改进算法的代码：

如改进的灰狼、鲸鱼和哈里斯鹰，但由于算法的随机性，其结果并不能每次都是算法中的最优，因此若想要该部分算法的可以和作者了解一下再决定，获取方式：

引入MSGWO的UAV —— GZH（KAU的云实验台）后台回复

UAVGWO

引入AAMCWOA的UAV —— GZH（KAU的云实验台）后台回复

UAVWOA

引入SDMQHHO的UAV —— GZH（KAU的云实验台）后台回复

​UAVHHO

参考文献

[1]PHUNG M D, HA Q P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization [J]. Ap⁃ plied Soft Computing, 2021, 107: 107376.

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞/再看 (ง •̀_•́)ง(不点也行)，若有定制需求，可私信作者。