八大算法排序@快速排序、递归版本一(C语言版本)
目录
- 快速排序版本一
-
- 概念
- 算法思想
-
- 一
- 二
- 三
- 快排步骤
- 代码实现
- 时间复杂度
- 空间复杂度
- 特性总结
快速排序版本一
概念
快速排序(Quicksort)是一种高效的排序算法,它是由英国计算机科学家 Tony Hoare 在1960年提出的。快速排序是基于分治(Divide and Conquer)策略的算法,其基本思想是通过选择一个基准元素,将数组划分为两个子数组,使得左侧子数组的元素都小于基准元素,右侧子数组的元素都大于基准元素,然后对子数组进行递归排序。
快速排序的核心算法有多种实现方法,该文章介绍的版本是。借助双指针,递归的方式实现排序功能。
算法思想
(
注:为了方便理解,下文所说的指针,并不是概念上的指针,其实就是一个变量,只是为了更加形象的表达、讲解,所以用了指针这一形象的工具。
)
原数组使用变量left 、 right 记录数组第一个和最后一个元素的下标。借助快排核心算法:
在数组中选取一个元素,作为基准值。使用 “双指针” 分别从数组的左边和右边开始往中间挪动,要求:
左边的 “指针” begin 从左到右寻找到比基准值大的数则停止,右边的 “指针” end 从右到左寻找到比基准值小的数则停止。 接着左右指针指向的数据互换。交换完成后,左边 ”指针” 继续往右边寻找,右边 “指针” 继续往左边寻找。
重复以上的动作,直到 begin“指针” 和 end “指针”相遇,交换begin 和 end所指的元素(自身交换),然后结束退出迭代过程。最后将一开始选定的基准值与左 “指针” begin指向的数据进行交换。
最终的结果:最终与begin “指针” 所指的位置交换后的基准值,基准值左边的数都比基准值小,右边的数都比基准值大。假设数组排好升序的情况下,基准值所在的位置,便是升序下所在的位置。即根据以上的步骤,我们便完成数组中的一个元素(基准值)的排序。
接着用变量div存储begin“指针”指向的下标,根据这个下标,将原数组一分为二,分别为[left , div-1] 、[div+1,right]。然后依次对这两个数组进行以上快排的核心算法,也就是递归的思想。通过每次递归一次完成一个“基准值”到达指定的位置。最终实现了整个数组的排序。
为了方便演示递归的流程,使用数组arr[] = { 6 , 2 , 3 , 9 , 4 } 进行升序过程的模拟实现。
一
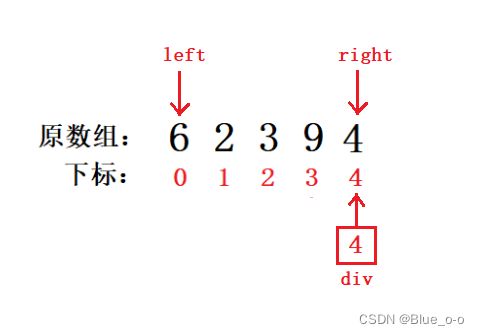
一开始用变量left、right 存储待排序数组的第一个元素下标和最后一个元素的下标。div变量用来接收快排核心算法最终返回的begin存储的下标。
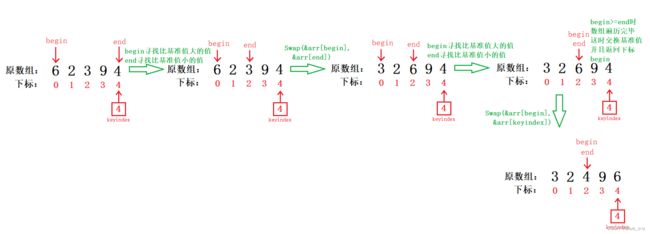
将数组的地址、待排序数组 left 和 right 传入核心算法函数,核心算法思路图解如下:
基准值一般选取待排序数组的最后一个元素的下标,如图选取元素4作为基准值。
begin指向的下标0的元素6比4大,begin“指针”停止。
end指向的下标4的元素4没比基准值小,所以接着往左边找,直到end指向下标为2的元素3满足条件,end “指针” 停止。
接着begin 和 end 指向的两个元素交换。交换后重复迭代动作。
交换后的begin指针指向的元素从原来的6变成了3,不满足条件,所以接着往右边寻找,直到指向下标为2的元素6时才满足停止的条件,但是这时begin “指针” 和 end “指针” 相遇了,因此退出迭代,最终begin “指针” 指向的元素和基准值进行交换。
最终返回begin变量存储的下标值。
退出核心排序算法函数后,如下:

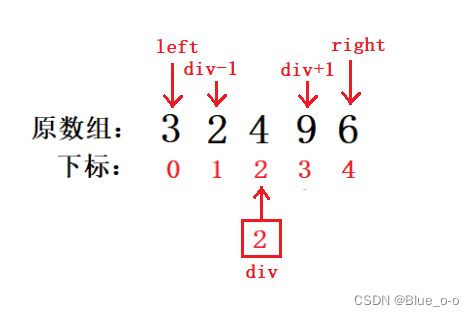
变量div接收核心排序算法函数返回的begin变量存储的下标值。这时,我们已经完成了对数组升序结果中,元素4的排序了。
接着将数组,以div所指的位置为分割点,划分为两个数组,分别为 [ left,div-1] 、[ div+1,right]。如下:
现在问题从,对数组arr[] = { 6 , 2 , 3 , 9 , 4 }的升序排序,转变为对数组 { 3 , 2 } 和 { 9 , 6 } 的升序排序了。但是对于这两个待排序的数组,排序的思路和上述的思路一致,借助 “双指针” 的方法,一步步递归下去,最终由一个个排好序的个体,返回到原数组时,形成有序的整体。
二
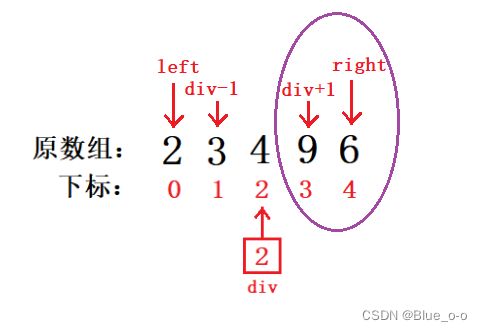
对于分割出来的数组的排序流程如下:
传入数组arr的地址,left 和 div-1给核心算法函数:
begin所在的元素比基准值2大,故停止不动;
end所在的元素没比基准值小,故向左移动,当指向下标0时,与begin “指针” 相遇,begin 和 end 所指的元素交换,而后结束、退出迭代过程。
最终begin指向的元素和基准值进行交换,然后返回begin存储的下标值。
退出核心算法函数,如下:

又实现了对于 [ left,div-1] 数组的排序。
注意:这里还需递归一次,但是可以通过边界判断直接返回。
三
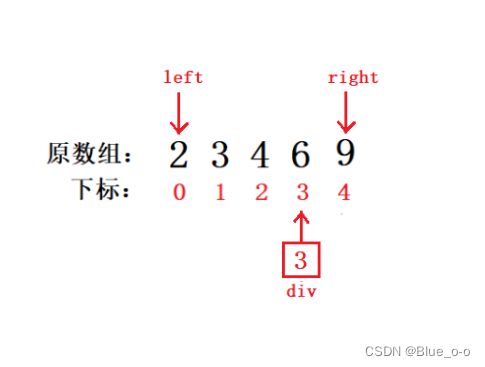
同样的思路,对 [ div+1,right ] 所处的数组进行排序:
传入数组arr的地址,div+1 和 riht 下标范围,如下:
退出核心算法后:
后续,主要为返回递归,销毁调用的栈帧,回到一开始调用的函数。结束排序。
最后,实现了整个数组的升序排序效果。以上是对于“双指针版本” 的快速排序的大体流程讲解。
具体步骤如下。
快排步骤
基本步骤:
1、选择基准元素: 从数组中选择一个元素作为基准元素。选择基准元素的方法可以有多种,常见的包括选择第一个元素、最后一个元素或随机选择一个元素。
2、划分数组: 将数组中的其他元素按照与基准元素的大小关系分为两个子数组。比基准元素小的放在左侧,比基准元素大的放在右侧。相等的元素可以放在任一侧。
3、递归排序: 对左右两个子数组进行递归排序。递归的终止条件是子数组的大小为1或0,因为一个元素或没有元素的数组是已经有序的。
4、合并结果: 将排好序的左右子数组合并成最终的有序数组。
代码实现
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
// 三数取中法,排除 key 取到最大 和 最小的数值
// 如数组: 0 1 2 3 4 5 6 7 8 9 时 中间值为4,随后将 4 和 9 互换,再进行快排,即可将最坏的情况变为最优情况
int GetMidIndex(int* a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] < a[mid])
{
if (a[mid] < a[end])
{
return mid;
}
else if (a[begin] > a[end])
{
return begin;
}
else
{
return end;
}
}
else //a[begin] > a[mid]
{
if (a[mid] > a[end])
{
return mid;
}
else if (a[begin] < a[end])
{
return begin;
}
else
{
return end;
}
}
}
// 时间复杂度:O(N)
// [begin,end] 1、左右指针法
int PartSort1(int* a, int begin, int end)
{
int midIndex = GetMidIndex(a, begin, end);
Swap(&a[midIndex], &a[end]); // 让最坏的情况不再会出现
int keyindex = end;
while (begin < end)
{
// 注意:此处 要给个‘=’,若不然当左右第一找到的数都是a[keyindex] 会一直死循环
while (begin < end && a[begin] <= a[keyindex])
{
begin++;
}
while (begin < end && a[end] >= a[keyindex])
{
end--;
}
Swap(&a[begin], &a[end]);
}
Swap(&a[begin], &a[keyindex]);
return begin;
}
/*
极端情况下,快速排序最坏的情况下,
每次选到的key都是最大的或者最小的 (有序或者接近有序)
时间复杂度:O(N^2)
最好情况下:
时间复杂度:(类似于将N个数分散到二叉树中,高度为logN,每一层时间复杂度为 N )
所以时间复杂度为:O( N*logN )
空间复杂度:O(logN)
*/
// 快速排序 单趟排序
void QuickSort(int* a, int left, int right)
{
assert(a);
if (left >= right) return;
if ((right - left + 1) > 10)
{
int div = PartSort1(a, left, right);
//PrintArr(a + left, right - left + 1);
//printf("[%d,%d]%d[%d,%d]\r\n", left, div - 1, div, div + 1, right);
QuickSort(a, left, div - 1);
QuickSort(a, div + 1, right);
}
else
{
// 小于等于10以内的数组,不再使用递归排序
// 小区间使用插入排序去排,不再使用快速排序的递归排
// 减少整体的递归次数
InsertSort(a + left, right - left + 1);
}
}
以上是关于快速排序,核心算法版本一“双指针”的演示流程和代码。可以结合这图形和代码自己演示一遍,更有利于理解。难点主要是递归的思想,需要注意是:
1、递归过程中核心思想是相同的,
2、注意递归返回的判定条件,防止出现栈溢出问题。
上述代码还有一点没讲到:
三树取中法。主要是防止,每次的基准值取到的是数组中最大/最小的元素。如升序排序时,基准值每次取到的都是最大值的话,左 “指针” begin就得一直从左找到右,begin和end相遇了才退出;若基准值每次取到的都是最小值的话,那么右 “指针” 又得一直从右找到左,知道end和begin相遇才退出。这样就会大大的拉低程序的效率。
至此,我们发现如果原数组一开始便是有序的,比如 arr = { 2 , 3 , 4 , 6 , 9 },如果没有使用三树取中法的话,那么将出现最坏的情况,快排效率为O(N^2);
但是如果使用了三树取中法,取左右两边和中间的三个数中的既不是最大也不是最小的数,作为基准值。如{ 2 , 3 , 4 , 6 , 9 }这种情况,将 4 和 9 互换,4作为基准值,那么原先最坏的情况,将变成最好的情况,时间复杂度为O(N^logN)。
除此之外,对于数组较小的排序,可以采用其他的排序方法,进行排序。因为快速排序得使用到递归,在性能上会造成栈帧上的开销。因此对于较小的数组排序时可以借助其他排序,上述代码使用的是插入排序。
时间复杂度
O( N*logN )
计算如下:

快排有点类似于将数组放到一个二叉树上,
在第一层选取1个元素排序、
在第二层选取2个元素排序、
在第三层选取4个元素排序、
…
在第n蹭选取2^(n-1)个元素排序。
每一层,都需要遍历一遍待排序的数组,大体上归纳统计,每一层时间复杂度为O(N)。
而整个“二叉树” 的高度为 logN。
所以时间复杂度为:O(N*logN)。
以上画的是理想下,每次都是均匀划分的。
空间复杂度
O(logN)
递归需要调取栈帧,递归的深度是logN,每次递归使用的空间是常数量O(1)。
所以空间上开销为:1*logN。
即空间复杂度为:O(logN)。
特性总结
1、快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
2、时间复杂度:O(N*logN)
3、 空间复杂度:O(logN)
4、稳定性:不稳定