Bellman-ford算法

目录

算法分析

有边数限制的最短路

---

算法分析

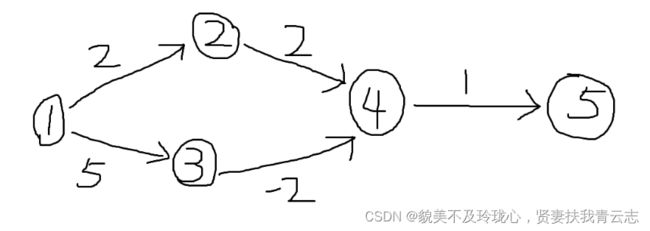
问题：为什么Dijkstra不能使用在含负权的图中？

Dijkstra算法的3个步骤

• 找到当前未标识的且离源点最近的点t
• 对t号点点进行标识
• 用t号点更新其他点的距离

反例：

结果：dijkstra算法在图中走出来的最短路径是1 -> 2 -> 4 -> 5，算出 1 号点到 5 号点的最短距离是2 + 2 + 1 = 5，然而还存在一条路径是1 -> 3 -> 4 -> 5，该路径的长度是5 + (-2) + 1 = 4，因此 dijkstra 算法失效

dijkstra详细步骤

• 初始dist[1] = 0
• 找到了未标识且离源点1最近的结点1，标记1号点，用1号点更新其他所有点的距离，2号点被更新成dist[2] = 2，3号点被更新成dist[3] = 5
• 找到了未标识且离源点1最近的结点2，标识2号点，用2号点更新其他所有点的距离，4号点被更新成dist[4] = 4
• 找到了未标识且离源点1最近的结点4，标识4号点，用4号点更新其他所有点的距离，5号点被更新成dist[5] = 5
• 找到了未标识且离源点1最近的结点3，标识3号点，用3号点更新其他所有点的距离，4号点被更新成dist[4] = 3
• 结束
• 得到1号点到5号点的最短距离是5，对应的路径是1 -> 2 -> 4 -> 5，并不是真正的最短距离

问题：什么是bellman - ford算法？

bellman - ford算法擅长解决有边数限制的最短路问题

Bellman - ford 算法是求含负权图的单源最短路径的一种算法，效率较低，代码难度较小。其原理为连续进行松弛，在每次松弛时把每条边都更新一下，若在 n-1 次松弛后还能更新，则说明图中有负环，因此无法得出结果，否则就完成。

(通俗的来讲就是：假设 1 号点到 n 号点是可达的，每一个点同时向指向的方向出发，更新相邻的点的最短距离，通过循环 n-1 次操作，若图中不存在负环，则 1 号点一定会到达 n 号点，若图中存在负环，则在 n-1 次松弛后一定还会更新)

bellman - ford算法的具体步骤

for n次
        for 所有边 a,b,w (松弛操作)
                dist[b] = min(dist[b],back[a] + w)

注意：back[] 数组是上一次迭代后 dist[] 数组的备份，由于是每个点同时向外出发，因此需要对 dist[] 数组进行备份，若不进行备份会因此发生串联效应，影响到下一个点

在下面代码中，是否能到达n号点的判断中需要进行if(dist[n] > INF/2)判断，而并非是if(dist[n] == INF)判断，原因是INF是一个确定的值，并非真正的无穷大，会随着其他数值而受到影响，dist[n]大于某个与INF相同数量级的数即可

有边数限制的最短路

板子

int n, m;       // n表示点数，m表示边数
int dist[N];        // dist[x]存储1到x的最短路距离

struct Edge     // 边，a表示出点，b表示入点，w表示边的权重
{
    int a, b, w;
}edges[M];

// 求1到n的最短路距离，如果无法从1走到n，则返回-1。
int bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    // 如果第n次迭代仍然会松弛三角不等式，就说明存在一条长度是n+1的最短路径，由抽屉原理，路径中至少存在两个相同的点，说明图中存在负权回路。
    for (int i = 0; i < n; i ++ )
    {
        for (int j = 0; j < m; j ++ )
        {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            if (dist[b] > dist[a] + w)
                dist[b] = dist[a] + w;
        }
    }

    if (dist[n] > 0x3f3f3f3f / 2) return -1;
    return dist[n];
}

void bellman_ford()
{
	memset(dist,0x3f,sizeof dist);
	dist[1]=0;
	for(迭代k)   //这个算法是用来处理有边数限制的最短路
	{
		for(迭代所有的边)//使用边来更新距离。
			memcpy(last, dist, sizeof dist);
			dist[e.b] = min(dist[e,b],last[e.a]+e.c);//a可能已经被更新了需要一个数组记录之前的状态。
	}
}

 思路：

1. 第一层for循环迭代经过最多的边数，k的每个值，dist[]的状态对应

2. 第二层for循环迭代所有的边，更新所有点的最短距离

3. 每次更新边需要k-1的个状态，也就是last数据记录的数据dist[e.b] = min(dist[e.b], last[e.a] + e.c)；

4. 1----2----3 当2----3 更新dist[3]=0x3f 此时k=1 也就说明走一次，3走不到，更新不到边但k=2 last数组记录了k=1时的dist， 此时可以由2更新3的点

这个算法for循环迭代所有的边每次使用边更新每个点到1这个点的距离，更新几次就是最小变数的dist[n]

解题代码：

#include 
#include 
#include 

using namespace std;

const int N = 510, M = 10010;

struct Edge
{
    int a, b, c;
}edges[M];

int n, m, k;
int dist[N];
int last[N];

void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);

    dist[1] = 0;
    for (int i = 0; i < k; i ++ )
    {
        memcpy(last, dist, sizeof dist);
        for (int j = 0; j < m; j ++ )
        {
            auto e = edges[j];
            dist[e.b] = min(dist[e.b], last[e.a] + e.c);
        }
    }
}

int main()
{
    scanf("%d%d%d", &n, &m, &k);

    for (int i = 0; i < m; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        edges[i] = {a, b, c};
    }

    bellman_ford();

    if (dist[n] > 0x3f3f3f3f / 2) puts("impossible");
    else printf("%d\n", dist[n]);

    return 0;
}