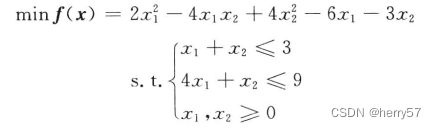优化-规划问题（数学建模）

目录

一.线性规划

1.求最小值

2.最大值

二.二次规划 

1.概念：目标函数是决策向量的二次函数，约束条件都是线性的。

2.最小值

3.最大值.

三.整数规划

 1.整数线性规划（决策变量中部分或者全部取整数，对结果值不要求）

2.0-1整数线性规划

3.非线性整数规划-模特卡罗法

 四.非线性规划

1.有约束极值问题

 2.无约束极值问题

---

 

一.线性规划

1.求最小值

clc,clear
prob=optimproblem;%默认目标函数最小化
x=optimvar('x',3,1,'LowerBound',0);%决策变量3*1
prob.Objective = -5*x(1)-4*x(2)-6*x(3);%目标函数
%约束条件
prob.Constraints.cons1 = x(1)-x(2)+x(3)<=20;
prob.Constraints.cons2 = 3*x(1)+2*x(2)+4*x(3)<=42;
prob.Constraints.cons3 = 3*x(1)+2*x(2)<=30;
[sol,fval,flag,out]=solve(prob)
sol.x

结果：

ans =

         0
   15.0000
    3.0000

fval =

   -78

out = 

  包含以下字段的 struct:

         iterations: 3
    constrviolation: 0
            message: 'Optimal solution found.'
          algorithm: 'dual-simplex'
      firstorderopt: 1.7764e-15
             solver: 'linprog'

2.最大值

clc,clear
prob=optimproblem('ObjectiveSense','max');
x=optimvar('x',3,1,'LowerBound',0);
prob.Objective = 2*x(1)+3*x(2)-5*x(3);
prob.Constraints.cons1 = x(1)+x(2)+x(3)==7;
prob.Constraints.cons2 = 2*x(1)-5*x(2)+x(3)>=10;
prob.Constraints.cons3 = x(1)+3*x(2)+x(3)<=12;
[sol,fval,flag,out]=solve(prob)
sol.x

结果：

fval =

   14.5714
ans =

    6.4286
    0.5714
         0

二.二次规划 

1.概念：目标函数是决策向量的二次函数，约束条件都是线性的。

2.最小值

clc,clear
prob=optimproblem;%默认目标函数最小化
x=optimvar('x',2,1,'LowerBound',0);%决策变量3*1
prob.Objective = 2*x(1)^2-4*x(1)*x(2)+4*x(2)^2-6*x(1)-3*x(2);%目标函数
%约束条件
prob.Constraints.cons1 = x(1)+x(2)<=3;
prob.Constraints.cons2 = 4*x(1)+x(2)<=9;
[sol,fval,flag,out]=solve(prob)
sol.x

结果:

ans =

    1.9500
    1.0500

fval =

  -11.0250

3.最大值.

max  f=-x(1)^2-0.3*x(1)*x(2)-2*x(2)^2+98*x(1)+277*x(2)

x(1)+x(2)<=100;

x(1)-2*x(2)<=0;

x(1),x(2)>=0

 clc,clear,format long g
prob=optimproblem('ObjectiveSense','max');
x=optimvar('x',2,1,'LowerBound',0);
prob.Objective = -x(1)^2-0.3*x(1)*x(2)-2*x(2)^2+98*x(1)+277*x(2);
prob.Constraints.cons1 = x(1)+x(2)<=100;
prob.Constraints.cons2 = x(1)-2*x(2)<=0;
[sol,fval,flag,out]=solve(prob)
sol.x
format short %恢复到短小数的显示格式

结果：

ans =

          35.3703703701727
          64.6296296287408

fval =

          11077.8703703618

三.整数规划

 1.整数线性规划（决策变量中部分或者全部取整数，对结果值不要求）

 clc, clear,
prob = optimproblem;
x = optimvar('x',6,'Type','integer','LowerBound',0);
prob.Objective = sum(x);
prob.Constraints.cons1 = x(1)+x(6)>=35;
prob.Constraints.cons2 = x(1)+x(2)>=40;
prob.Constraints.cons3 = x(2)+x(3)>=50;
prob.Constraints.cons4 = x(3)+x(4)>=45;
prob.Constraints.cons5 = x(4)+x(5)>=55;
prob.Constraints.cons6 = x(5)+x(6)>=30;
[sol,fval,flag,out]=solve(prob)
sol.x

结果：

ans =

    35
     5
    45
     0
    55
     0

fval =

   140

2.0-1整数线性规划

 

 clc, clear, 
c = [15 13.8 12.5 11 14.3
    14.5 14 13.2 10.5 15
    13.8 13 12.8 11.3 14.6
    14.7 13.6 13 11.6 14];
prob = optimproblem;
x = optimvar('x',4,5,'Type','integer','LowerBound',0,'UpperBound',1);
prob.Objective = sum(sum(c.*x));
prob.Constraints.con1 = sum(x,1)==1;
prob.Constraints.con2 = sum(x,2)<=2;
[sol, fval, flag] = solve(prob)
sol.x

结果：

ans =

     0     0     1     0     0
     0     0     0     1     0
     1     1     0     0     0
     0     0     0     0     1

fval =

   63.8000

3.非线性整数规划-模特卡罗法

 

clc, clear

%rng('shuffle')  %根据当前时间为随机数生成器提供种子

rng(0) %进行一致性比较，每次产生的随机数是一样的

p0=0; n=10^6; tic    %计时开始

for i=1:n

   x=randi([0,99],1,5); %产生一行五列的区间[0,99]上的随机整数

   [f,g]=mengte(x);

   if all(g<=0)

       if p0

           x0=x; p0=f; %记录下当前较好的解

       end

   end

end

x0, p0, toc    %计时结束

function [f,g]=mengte(x)  %定义目标函数和约束条件

f=x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)-8*x(1)-2*x(2)-3*x(3)-...

x(4)-2*x(5);

g=[sum(x)-400

x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800

2*x(1)+x(2)+6*x(3)-200

x(3)+x(4)+5*x(5)-200];

end

 结果：

x0 =

    46    98     1    99     3

p0 =

       50261

历时 1.391515 秒。

 四.非线性规划

1.有约束极值问题

 clc, clear, prob = optimproblem;
x = optimvar('x',3,'LowerBound',0);
prob.Objective = sum(x.^2)+8;
prob.Constraints.con1 = -x(1)^2+x(2)-x(3)^2 <= 0;
prob.Constraints.con2 = x(1)+x(2)^2+x(3)^3 <= 20;
prob.Constraints.con3 = -x(1)-x(2)^2+2 == 0;
prob.Constraints.con4 =  x(2)+2*x(3)^2 == 3;
x0.x=rand(3,1);  %非线性规划必须赋初值
[sol,fval,flag,out]= solve(prob,x0), sol.x

结果：

ans =

    0.5522
    1.2033
    0.9478

fval =

   10.6511

 2.无约束极值问题

 clc, clear, prob=optimproblem;  %最小值问题
x=optimvar('x',2); 
prob.Objective = 100*(x(2)-x(1)^2)^2+(1-x(1))^2;
x0.x=rand(2,1)  %初始值
[sol,fval,flag,out]=solve(prob,x0), sol.x

 结果：

ans =

    1.0000
    1.0000

fval =

   1.2326e-30

 clc, clear, prob1=optimproblem;  %最小值问题
x=optimvar('x','LowerBound',-3,'UpperBound',3);
y=optimvar('y','LowerBound',-4,'UpperBound',4);
prob1.Objective=x^3-y^3+3*x^2+3*y^2-9*x;
x0.x=1; x0.y=1;
[sol1,fval1,flag1,out1]=solve(prob1,x0)
prob2=optimproblem('ObjectiveSense','max')
prob2.Objective=x^3-y^3+3*x^2+3*y^2-9*x;
op=optimoptions(@fmincon,'Algorithm','active-set')
[sol2,fval2,flag2,out2]=solve(prob2,x0,'Options',op)

结果：

最小值：

 x: 1.0000
 y: 1.7072e-10

fval1 =

    -5

最大值：

 x: 1
 y: 2.0000
fval2 =

   -1.0000