每天刷两道题——第七天+第八天

力扣官网

1.1移动零

给定一个数组$nums$，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序，在不复制数组的情况下原地对数组进行操作。

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

代码

 def moveZeroea(self,nums):
        if not nums:
            return 0
        j=0
        # 将所有非零的元素依次提前，最后将剩下的全修改为0
        for i in range(len(nums)):
            if nums[i]!=0:
                nums[j]=nums[i]
                j+=1
        for i in range(j,len(nums)):
            nums[i]=0
        return nums

1.2盛最多水的容器

给定一个长度为$n$的整数数组 $height$ 。有 $n$ 条垂线，第 $i$ 条线的两个端点是 $(i,0)$ 和 $(i,height[i])$ 。找出其中的两条线，使得它们与 $x$ 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。说明：你不能倾斜容器。

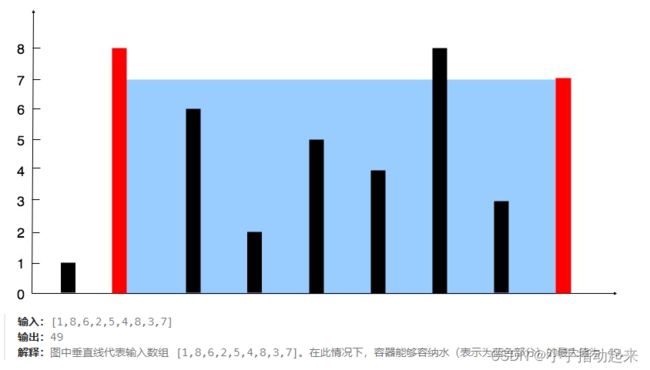
输入：[1,8,6,2,5,4,8,3,7]
输出：49

设两指针$i,j(j>i)$指向的水槽板高度分别为 $h[i],h[j]$ ，此状态下水槽面积为 S(i,j) 。由于可容纳水面积如下 ：
$S(i,j)=min(h[i],h[j])\times (j-i)$

在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽 底边宽度−1：
1.若向内 移动短板 ，水槽的短板 $min(h[i],h[j])$ 可能变大，因此下个水槽的面积 可能增大 。
2.若向内 移动长板 ，水槽的短板$min(h[i],h[j])$​ 不变或变小，因此下个水槽的面积 一定变小 。
因此，初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积。

代码

 def maxArea(self,height):
        i,j,ares=0,len(height)-1,0
        while i<j:
            if height[i]<height[j]:
                ares=max(ares,height[i]*(j-i))
                i+=1
            else:
                ares=max(ares,height[i]*(j-i))
                j-=1
        return ares

1.3三数之和

给你一个整数数组 $nums$ ，你返回所有和为 0且不重复的三元组 $[nums[i],nums[j],nums[k]]$ 满足 $i!=j、i!=k且j!=k$ ，同时还满足 $nums[i]+nums[j]+nums[k]==0$ 。

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。(和1重复了)
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。

 def treeSum(self,nums):
        res=[]
        n=len(nums)
        if (not nums or n<3): #数组为空或者长度小于3
            return []
        nums.sort()  #=升序排序 ，nums.sort(reverse=True)=降序排序
        for i in range(n):
            if nums[i]>0:#如果第一个元素超过零了，后面找不出两个和他相加等于零的数了
                return res
            if i>0 and nums[i]==nums[i-1]:
                continue
            l=i+1
            r=n-1
            while l<r:
                if nums[i]+nums[l]+nums[r]==0:
                    res.append([nums[i],nums[l],nums[r]])
                    while l<r and nums[l]==nums[l+1]:
                        l=l+1
                    while l<r and nums[r]==nums[r-1]:
                        r=r-1
                    l=l+1
                    r=r-1
                elif nums[i]+nums[l]+nums[r]>0:
                    r=r-1
                else:
                    l=l+1
        return res

1.4接雨水

给定 $n$ 个非负整数表示每个宽度为 $1$ 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

栈

类似于括号匹配，仔细观察蓝色的部分，每次匹配出一对括号（找到对应的一堵墙），就计算这两堵墙中的水。

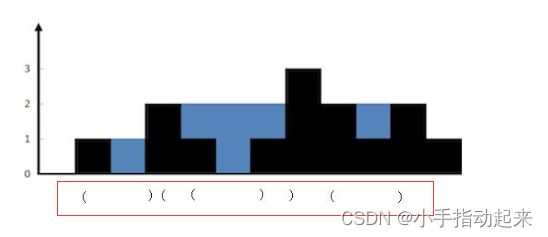
用栈保存每堵墙。当遍历墙的高度的时候，如果当前高度小于栈顶的墙高度，说明这里会有积水，我们将墙的高度的下标入栈。如果当前高度大于栈顶的墙的高度，说明之前的积水到这里停下，我们可以计算下有多少积水了。计算完，就把当前的墙继续入栈，作为新的积水的墙。

步骤为：
1.当前高度小于等于栈顶高度，入栈，指针后移。
2.当前高度大于栈顶高度，出栈，计算出当前墙和栈顶的墙之间水的多少，然后计算当前的高度和新栈的高度的关系，重复第 2 步，直到当前墙的高度不大于栈顶高度或者栈空，然后把当前墙入栈，指针后移。

代码：

class stack:
    def __init__(self,size):
       self.max=size  #栈的容量
       self.elem=[None]*self.max
       self.top=0  #栈顶
       self.base=0  #栈尾

    def push(self,num):
        if self.top-self.base==self.max:
            print("the stack is full")
        self.elem[self.top]=num
        self.top+=1

    def pop(self):
        if self.top==self.base:
            print("the stack is empty")
        self.top-=1
        e=self.elem[self.top]
        return e

    def get_pop(self):
        return self.elem[self.top-1]

    def isEmpty(self):
        if self.top==self.base:
            return True
        else:
            return False

class question:
    def trap(self,height):
        sum=0
        hstack=stack(len(height))
        i=0
        while i<len(height):
            #如果栈不为空，并且指向高度大于栈顶的高度就一直循环
            while not hstack.isEmpty() and height[i]>height[hstack.get_pop()]:
                h=height[hstack.get_pop()] #栈顶元素
                hstack.pop()
                if hstack.isEmpty():
                    break
                distance=i-hstack.get_pop()-1  #两墙之间的距离
                dmin=min(height[hstack.get_pop()],height[i])
                sum=sum+distance*(dmin-h)  #距离乘以当前元素和栈顶元素的差值
            hstack.push(i) #当前指针入栈
            i+=1  #指针后移
        return sum