【数模百科】支持向量机SVM如何处理非线性数据——非线性SVM
本篇文章摘录自 非线性SVM - 数模百科，里面有非常详细的对SVM模型以及各种延伸模型的讲解，涵盖了所有的知识点以及重点，包括代码讲解。
如果你对支持向量机SVM模型还不清楚，建议先阅读这篇文章 【数模百科】支持向量机中的线性SVM讲解以及实现办法-CSDN博客
你在玩一个分类游戏，游戏里，你面前有一大堆彩色的小球。这些小球有红的、蓝的、绿的，各种颜色都有。你的任务就是要把同一个颜色的小球聚在一起。有时候游戏很简单，比如说红球都在左边，蓝球都在右边，你可以拿根直直的棍子一挥，就能轻松把它们分开。
但有时候游戏会变得复杂，小球们像过家家一样，全都挤在一起，红蓝绿黄挨个儿搅和在一块儿，这时候你要做的就不是简单地用直棍子一分了之了。你得找到一条能把同色小球串联起来的路径，而这条路又不能擦到其他颜色的小球。这条路可能是弯弯曲曲的，就像山路十八弯，得蜿蜒曲折着穿过一片小球的海洋。
想象一下，如果这根棍子能根据需要弯曲成任意形状，它就能像个魔术师一样，变出最合适的形状，准确无误地把小球们分开。它就像有了魔法，总能找到一个完美的姿势，贴着同色小球的边缘走，同时又尽量远离其他颜色的小球。
这个游戏里的棍子，其实就像是我们数学里的一个数学模型——非线性支持向量机。它就有这样的魔法能力，在一大堆复杂混乱的数据中，找到一个最好的方法，把不同的数据分得清清楚楚、明明白白。就是说，无论情况有多复杂，它都能巧妙地解决问题，让不同类别的数据各归各位。
定义与详解
定义
非线性支持向量机，是从原始的线性支持向量机演化而来的，与线性支持向量机的主要区别在于它可以处理非线性可分的数据集。这是通过使用一种所谓的“核技巧（Kernel trick）”来实现的。
原始的线性支持向量机试图在样本的特征空间中寻找一个线性超平面，可以最大化地分隔两个类别的样本。然而，在实际情况中，我们经常会遇到一些问题，其中两个类别的样本无法通过一个线性超平面来完全分隔。
为了解决这个问题，非线性支持向量机的方法是将样本从原始的特征空间映射到一个更高维的空间，希望在这个新的高维空间中，样本可以被一个线性超平面分隔。为了避免在高维空间中进行复杂的计算，人们引入了核函数来隐式地执行这种映射操作，这就是所谓的“核技巧”。
常用的核函数包括以下：
-
齐次多项式核： 齐次多项式核的形式为：
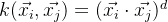，这是一个简单的多项式映射，将特征映射到 d 次多项式空间。 -
非齐次多项式核： 非齐次多项式核函数形式为：
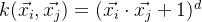。与齐次多项式核不同，非齐次多项式核在计算内积时添加了常数项1。 -
高斯径向基函数核（Radial basis function，RBF）： RBF核函数形式为：
。这是一个非线性映射，它将每一个特征向量映射到一个无限维的空间。 -
双曲正切核： 双曲正切核函数形式为：
。符合某些条件时，它也可以用于支持向量机的核函数。 -
核函数与变换（
）函数的关系： 一般而言，核函数可以写作两个变换后的特征向量的内积：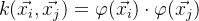
。在变换空间中的 w 可以写作
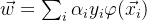。通过核技巧，我们能够将w 与 
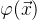的点积计算为
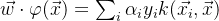，而无需显式计算变换函数。
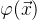它们分别对应着在不同的高维空间中寻找超平面的策略。通过灵活地选择和设计核函数，我们可以使非线性支持向量机在复杂的问题中得到良好的性能。
计算（软间隔）SVM分类器
计算软间隔SVM分类器的目标是使以下表达式最小化：
![\left[{\frac {1}{n}}\sum _{i=1}^{n}\max \left(0,1-y_{i}(\vec{w}\cdot \vec{x_{i}}+b)\right)\right]+\lambda \|w\|^{2}.](http://img.e-com-net.com/image/info8/3304930a094b499b90dc75b002f8ab7c.png){kind=small}
在上面的表达式中，如果选择足够小的 
值，那么当输入数据是可以线性分类的情况下，软间隔SVM将退化为硬间隔SVM。
接下来引入松弛变量 
，这是一个满足 
的最小非负数。将原来的目标函数转化为下面的优化问题，这叫做原型问题：
接下来，我们构造并求解拉格朗日对偶问题，得到下面简化的问题，这被称为对偶问题：
在这个对偶问题中，我们想找到变量 
，使我们的目标函数最大化。然后利用，我们可以计算出权重向量 w，
最后，对于给定的新数据点 z，其分类结果可以由决策函数
![sgn\left(\left[\sum_{i=1}^{n}c_{i}y_{i}k(x_{i},z)\right]+b\right),](http://img.e-com-net.com/image/info8/dfeb6f951bf04e7e98e36fa5ae69d4b6.png){kind=small}
得到。这里，
是核函数，将原始输入空间映射到更高维的特征空间。
这个过程中也用到了核技巧，这是因为在高维空间中直接计算可能会非常复杂，但是如果采用核函数，那么计算就大为简化，因为我们只需要计算核函数在原始输入空间中的值，而不需要直接在高维特征空间中进行操作。
优化算法
关于用于处理支持向量机（SVM）的两类优化算法：次梯度下降算法和坐标下降算法。这两种方法在处理大型稀疏数据集时，有显著的优势。
次梯度下降算法
次梯度下降方法是特别适用于存在大量训练实例的情况，该方法直接使用下面的函数进行优化：
![f(\vec{w},b) = \left[{\frac {1}{n}}\sum _{i=1}^{n}\max \left(0,1-y_{i}(w\cdot x_{i}+b)\right)\right]+\lambda \lVert w\rVert ^{2}.](http://img.e-com-net.com/image/info8/04bf8d8036c443e498aca07bdcd1ec64.png){kind=small}
这是一个凸函数，因此，我们可以使用梯度下降法或者随机梯度下降法（SGD）进行优化。但这里我们并不是在函数的梯度方向上前进，而是在次梯度中选择的方向上前进。次梯度是方向导数的上确界，比如在非可微点，梯度不存在，这时我们可以换成次梯度。该方法的优点是迭代次数不会随数据点数量的增加而增加。
坐标下降算法
该方法在处理特征空间维度高时特别有效。坐标下降法基于对偶问题，过程中会迭代更新每一个坐标，让目标函数值沿着当前坐标减少。
坐标下降方法的基本步骤如下：在每次迭代中，选择一个分量或坐标方向，然后固定其他所有坐标，只对这个坐标进行优化。这个过程会重复执行直到算法收敛。
具体来说，对于要最小化的目标函数 
，我们首先选择一个起始点 
，然后坐标下降法重复以下步骤直到收敛：
在第 k 步，选择坐标轴 j，更新 
，使得 f 在方向 j 上最小:
然后把其他的 w 保持不变。然后，我们再对一个不同的坐标轴进行相同的操作，直到满足某个收敛性的标准，或者到达了预设的最大迭代次数。
坐标下降法在处理大尺度且稀疏的, 特征维度很高的问题时，效率很高。 因为坐标下降法每次只操作一个坐标轴以降低问题的复杂性，而且可以利用稀疏性，只选择对函数值有影响的坐标进行优化。
代码
import numpy as np
from sklearn import svm, datasets
from sklearn.model_selection import train_test_split, GridSearchCV
import matplotlib.pyplot as plt
# 加载内置的鸢尾花数据
iris = datasets.load_iris()
X = iris.data[:, :2] # 只取前两个特征
y = iris.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 定义参数范围
param_grid = {'gamma': np.linspace(0.1,5,50)}
# 定义支持向量机和网格搜索
svc = svm.SVC(kernel='rbf')
grid_search = GridSearchCV(svc, param_grid, cv=5)
# 执行网格搜索
grid_search.fit(X_train, y_train)
# 输出最优参数
print('Best parameters: ', grid_search.best_params_)
# 使用最优gamma参数创建非线性SVM模型
model = svm.SVC(kernel='rbf', gamma=grid_search.best_params_['gamma'], C=1.0) # 使用高斯核
model.fit(X_train, y_train)
# 创造一个网格来画出图像
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# 在网格上进行预测
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 画图
# 详见数模百科
# 使用最优参数预测测试集
print('Accuracy of test set: ', model.score(X_test, y_test))这个代码首先对网格进行网格搜索以寻找最佳gamma参数，这个过程之后，我们使用找到的最优gamma参数创建一个SVM模型，并使用该模型来绘制决策边界图和预测测试集，最后输出预测测试集的准确率。图中不同的底色代表了SVM的训练结果的决策边界，不同颜色的点代表不同类别的训练数据点。
输出结果：
Best parameters: {'gamma': 0.2}
Accuracy of test set: 0.9
本篇文章来源于 非线性SVM - 数模百科
数模百科是一个由一群数模爱好者搭建的数学建模知识平台。我们想让大家只通过一个网站，就能解决自己在数学建模上的难题，把搜索和筛选的时间节省下来，投入到真正的学习当中。
我们团队目前正在努力为大家创建最好的信息集合，从用最简单易懂的话语和生动形象的例子帮助大家理解模型，到用科学严谨的语言讲解模型原理，再到提供参考代码。我们努力为数学建模的学习者和参赛者提供一站式学习平台，目前网站已上线，期待大家的反馈。
如果你想和我们的团队成员进行更深入的学习和交流，你可以通过公众号数模百科找到我们，我们会在这里发布更多资讯，也欢迎你来找我们唠嗑。