优化｜流形优化系列（一）

简介

流形优化是非线性优化的一个分支，它主要关注在特定的几何结构下进行优化。在流形优化中，优化问题通常是在黎曼流形上进行的，而非欧几里得空间。黎曼流形是带有黎曼度量的流形，该度量为流形上的每个点都定义了一个内积。这种内积结构提供了流形上测量长度和角度的方式，这在优化过程中非常重要，因为它允许我们定义梯度和Hessian等概念，并进行相应的优化操作。在流形优化的背景下，流形通常是解的约束集。例如，当解必须是正交矩阵、单位范数向量或其它特殊结构时，这些集合都可以被看作流形。对于连续优化，讨论多面体是考虑线性优化问题的基础，而在欧几里得空间中的微积分被用于发展非线性欧几里得优化理论。同样地，黎曼流形上的微积分，借助微分几何学（尤其是黎曼几何学）得以促进，对于黎曼流形上的优化是至关重要的。

流形优化相对于传统欧几里得空间上的优化方法，优势在于：

1. 在黎曼流形上迭代，减少建模误差，提高一些非线性问题的表示能力;
2. 充分利用目标函数的内在几何结构，通过选取合适的黎曼度量可将一些非凸优化问题转化为凸优化问题;
3. 保持最优化问题的尺度不变性。

在各个应用领域的需求牵引下，相关学者的研究工作极大地促进了黎曼流形优化理论的发展与工程应用，如Hermitian 特征值问题、自适应正则化、迹范数、相机位姿估计、经济负载分配、对称特征值问题、低秩矩阵填充等，其技术成果已成功应用于相关学科，如航空航天、理论物理、无线通信、医学成像、自动控制、计算机视觉等。

推荐感兴趣的同学阅读参考文献中的书目。

流形优化基础知识

从黎曼流形的概念开始，用 $\mathcal{M}$表示一个有限维的黎曼流形，并用 $T_p\mathcal{M}$ 表示 $\mathcal{M}$ 在点 $p$处的切平面。在 $\mathcal{M}$的每一点 $p$上，都有一个内积 $⟨\cdot ,\cdot {⟩}_p$定义在切空间 $T_p\mathcal{M}$上。黎曼度量 $⟨\cdot ,\cdot {⟩}_p$ 相关的范数记作 $\Vert \cdot {\Vert }_p$。用 $l(\gamma) $来表示分段光滑曲线 $\gamma :[a,b]\to \mathcal{M}$的长度。
流形优化的基本问题形式为：
$$\underset{x\in \mathcal{M}}{\min }f(x)$$

其中$f: \mathcal{M} \to \mathbb{R} $，$\mathcal{M}$是一个黎曼流形。

常见流形

以下是一些在流形优化中常用的流形例子：

1. 球面流形 (Sphere Manifold)：

   考虑单位球面 $S^{n-1}$ 在 ${\mathbb{R}}^n$ 中，定义为：
   $$S^{n-1}=\{x\in {\mathbb{R}}^n:\Vert x{\Vert }_2=1\}$$
   此流形上的点是具有单位范数的 ${\mathbb{R}}^n$ 中的向量。这是一个常见的约束，特别是在需要正则化或单位范数约束的优化问题中。

2. 正交流形 (Stiefel Manifold)：

   考虑所有有 $n$行和 $p$ 列的列正交矩阵的集合。它可以表示为：
   $$St(n,p)=\{X\in {\mathbb{R}}^{n\times p}:X^{T}X=I_p\}$$
   其中 $I_p$ 是 $p\times p$的单位矩阵。这种流形在子空间迭代和降维技术中很有用。

3. 正定锥流形 (Positive Definite Manifold)：

   考虑所有 $n\times n$正定矩阵的集合。这是一个在半正定编程和统计中非常重要的约束集。

4. Grassmann 流形：

   定义为 $n$ 维空间中所有 $p$ 维线性子空间的集合。与 Stiefel 流形相比，Grassmann 流形不考虑子空间的基的选取，只考虑子空间本身。

基础概念

当我们考虑流形优化问题时，特别是在黎曼流形上，优化的算法需要考虑流形的几何结构。为此，我们引入一些特定的概念，如黎曼梯度、收缩映射（retraction）和向量传输（vector transport）。以下是这些概念的定义：

1. 黎曼梯度 (Riemannian Gradient):

   对于定义在流形 $\mathcal{M}$上的实值函数 $f$，其在点$p$处的黎曼梯度，记作 ${\text{grad}}_{p}f$，是流形 $\mathcal{M}$上的一个切向量，与欧氏梯度 $\nabla f(p)$在该点的内积最大。数学上，它满足以下关系：
   $$⟨{\text{grad}}_{p}f,v{⟩}_p=D_{v}f(p),\forall v\in T_p\mathcal{M}$$

其中$D_{v}f(p)$是函数 $f$在点 $p$处沿着方向$v$的方向导数，而$⟨\cdot ,\cdot {⟩}_p$ 是点$p$处的黎曼度量。

2. 收缩 (Retraction):

   让我们从流形上的一点$p$开始，并考虑一个从该点出发的切向量$v$。收缩映射$R_p(v)$ 提供了一个近似的方法来移动到流形上另一点，从而在某种意义上对黎曼指数映射进行了近似。
   严格地说，对于给定的点$p$和切向量$v$，收缩映射$R_p:T_p\mathcal{M}\to \mathcal{M}$ 满足以下两个条件:

   -$R_p(0)=p$

   -$R_p$ 在$0$处是连续的

3. 传输 (Transport):

传输定义了如何将流形上一点的切空间中的向量“移动”到另一点的切空间中，而不改变其“方向”。设$T_p\mathcal{M}$和$T_q\mathcal{M}$ 分别是流形$\mathcal{M}$ 上点$p$和$q$的切空间，传输是一个映射：
$$T_p(v):T_p\mathcal{M}\to T_q\mathcal{M}$$
其中流形优化中两种常用的传输方式是：平行传输（parallel transport）和向量传输（vector transport）。

常见算法

有了上面提及的这些概念，类似欧式空间中的梯度下降法更新公式$x^{k+1}=x^k+t^k{d}^k$，我们可以简单的得到流形上的梯度下降算法的更新公式
$$x^{k+1}=R_x^k(-t^k{\text{grad}}_{x^k}f)$$
其中$t^k$是步长，$R_x^k$是在点$x^k$的收缩映射。

流形上的梯度下降法的关键在于如何正确地“移动”在流形上。由于流形的几何约束，我们不能简单地进行线性更新，而是需要利用流形的几何结构进行更新。黎曼梯度和收缩映射是这个过程中的核心组成部分。

近年来多种传统优化算法已成功地被扩展到流形优化领域，包括梯度下降，共轭梯度法，随机梯度下降法，牛顿法，信赖域法，内点法，BFGS和ADMM等。需要注意的区别是，流形上的梯度及Hessian矩阵信息也与流形本身有关（黎曼梯度和黎曼Hessian矩阵），同时更新过程也将依赖于收缩映射和传输，这些操作确保算法在流形的几何约束内进行迭代，并保持算法的稳定性和收敛性。因此，对流形及其相关知识的深入了解和熟悉变得尤为重要。

流形优化计算工具

Manopt

Manopt 是一个专门为研究人员和工程师设计的优化工具箱，旨在简化和推动定义在流形上的优化问题的解决过程。Manopt 提供了一系列工具和算法，帮助用户轻松地在各种流形结构上设置和解决优化问题。Manopt 的优势在于它的灵活性和易用性。它支持多种流形结构，如正定对称矩阵、Stiefel流形和球面流形等。此外，它的设计目标是为用户提供一个简单、直观的接口，使用户无需深入了解流形优化的复杂性就可以轻松应用。此外，Manopt 还拥有丰富的文档和教程，帮助新手快速上手，同时为经验丰富的研究者提供高级功能和自定义选项。

PyManopt是Manopt的Python版本，Manopt.jl是为Julia编程语言设计的Manopt版本。

实例

我们考虑Manopt官方给出的实例。计算对称矩阵 $A\in {\mathbb{R}}^{n\times n}$ 的主要特征向量。设 ${\lambda }_1\ge \cdots \ge {\lambda }_n$ 是其特征值。最大的特征值，${\lambda }_1$，是以下优化问题的最优值：
$$\underset{x\in {\mathbb{R}}^n,x\ne 0}{\max }\frac{x^{\top }Ax}{x^{\top }x}.$$
问题可以改写为：
$$\underset{x\in {\mathbb{R}}^n,\Vert x\Vert =1}{\min }-x^{\top }Ax.$$
函数及其在 ${\mathbb{R}}^n$ 中的梯度为：
$$\begin{array}{rl}f(x)& =-x^{\top }Ax,\\ \nabla f(x)& =-2Ax.\end{array}$$
向量 $x$ 的约束要求 $x$ 具有单位2-范数，即 $x$ 是球面上的一点：
$${\mathbb{S}}^{n-1}=\{x\in {\mathbb{R}}^n:x^{\top }x=1\}.$$
这是我们应用 Manopt 解决问题所需要的所有信息。

函数$f$在 ${\mathbb{S}}^{n-1}$ 上是光滑的。它在${\mathbb{S}}^{n-1}$上 $x$ 处的黎曼梯度 是 $x$ 处球的切线向量。它可以计算为从常规梯度 $\nabla f(x)$ 到该切线空间的投影，使用正交投影器 ${\mathrm{Proj}}_{x}u=(I-x{x}^{\top })u$：
$$\mathrm{grad}f(x)={\mathrm{Proj}}_x\nabla f(x)=-2(I-x{x}^{\top })Ax.$$
这是欧几里得梯度 $\nabla f$ 与黎曼梯度 $\mathrm{grad}f$ 之间的数学关系的一个示例，我们通常已经知道如何从微积分课程中计算 $\nabla f$，并且为优化需要 $\mathrm{grad}f$。在 Manopt 中，转换是在后台通过一个名为 egrad2rgrad 的函数完成的，我们只需要计算 $\nabla f$。

以下是使用Manopt 中的信赖域法解决这个优化问题的代码：

    % 生成随机问题数据
    n = 1000;
    A = randn(n);
    A = .5*(A+A.');

    % 创建问题结构
    manifold = spherefactory(n);
    problem.M = manifold;

    % 定义问题成本函数及其欧几里得梯度。
    problem.cost  = @(x) -x'*(A*x);
    problem.egrad = @(x) -2*A*x;% 注意 'e' 在 'egrad' 中代表欧几里得

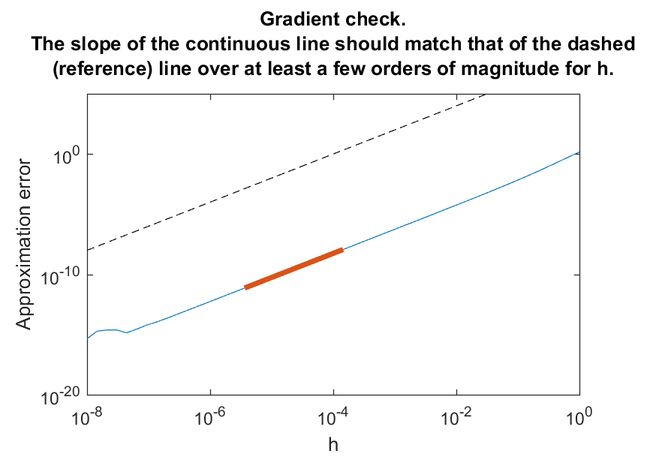
    % 数值检查梯度一致性（可选）
    checkgradient(problem);

    % 解决
    [x, xcost, info, options] = trustregions(problem);

    % 显示一些统计数据
    figure;
    semilogy([info.iter], [info.gradnorm], '.-');
    xlabel('迭代次数');
    ylabel('f 的梯度的范数');

运行结果：

在之后的系列中，我们会对上述提到的流形优化中的常见基本概念和算法进行详细的分析。

参考文献

1. Absil P A, Mahony R, Sepulchre R. Optimization algorithms on matrix manifolds[M]. Princeton University Press, 2008.
2. Boumal N. An introduction to optimization on smooth manifolds[M]. Cambridge University Press, 2023.
3. Sato H. Riemannian optimization and its applications[M]. Berlin: Springer, 2021.
4. 潘汉，黎曼流形优化及其应用, 北京, 科学出版社, 2020
5. 刘浩洋, 户将, 李勇锋，文再文，最优化：建模、算法与理论, 第二版草稿, 7.4 流形约束优化算法