代码随想录算法训练营第36天| 435. 无重叠区间 763.划分字母区间 56. 合并区间
JAVA代码编写
435. 无重叠区间
给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
示例 1:
输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: intervals = [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
提示:
1 <= intervals.length <= 105intervals[i].length == 2-5 * 104 <= starti < endi <= 5 * 104
教程:https://programmercarl.com/0435.%E6%97%A0%E9%87%8D%E5%8F%A0%E5%8C%BA%E9%97%B4.html
方法一:贪心
思路:和452. 用最少数量的箭引爆气球这一题很像,就是返回值不一样。
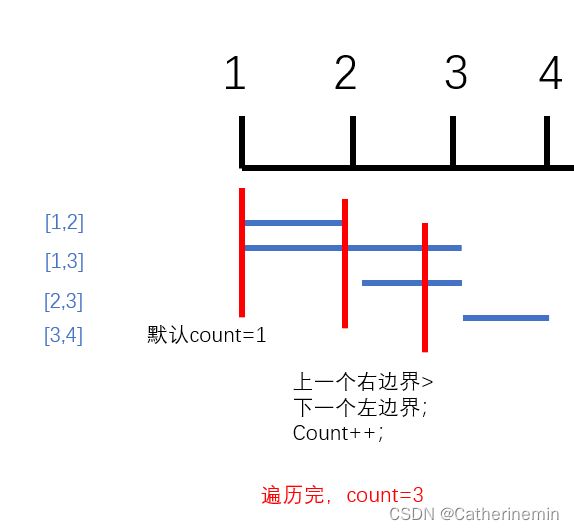
看看这个例子intervals = [[1,2],[2,3],[3,4],[1,3]]
步骤:
- 排序后是:
intervals = [[1,2],[1,3],[2,3],[3,4]] - 默认count是1(默认整个都是相交的),遍历intervals ,如果
上一个区间的右边界 大于 下一个区间的左边界,也就是上一个区间和下一个区间有交集,那就将这个两个中较小的值赋给当前区间的右边界;否则count++。 - 最后返回
intervals .length - count
复杂度分析:
- 时间复杂度:O(nlogn)
- 空间复杂度:O(n)
import java.util.Arrays;
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
// 排序方法1
// Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
// 排序方法2
Arrays.sort(intervals,(a,b)->a[0]-b[0]); // (a, b) 是传递给比较函数的两个参数,即数组中的两个元素。a[0] - b[0] 实际上是计算两个数组元素第一列值的差,如果结果为负数,则 a 应该排在 b 的前面;如果结果为正数,则 a 应该排在 b 的后面。
int count = 1;
for(int i = 1;i < intervals.length;i++){
if(intervals[i][0] < intervals[i-1][1]){
intervals[i][1] = Math.min(intervals[i - 1][1], intervals[i][1]);
continue;
}else{
count++;
}
}
return intervals.length - count;
}
public static void main(String[] args) {
int[][] intervals ={{1,2},{2,3},{3,4},{1,3}};
Solution solution = new Solution();
solution.eraseOverlapIntervals(intervals);
}
}
763.划分字母区间
给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。
注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。
返回一个表示每个字符串片段的长度的列表。
示例 1:
输入:s = "ababcbacadefegdehijhklij"
输出:[9,7,8]
解释:
划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的,因为划分的片段数较少。
示例 2:
输入:s = "eccbbbbdec"
输出:[10]
提示:
1 <= s.length <= 500s仅由小写英文字母组成
教程:
https://programmercarl.com/0763.%E5%88%92%E5%88%86%E5%AD%97%E6%AF%8D%E5%8C%BA%E9%97%B4.html
方法一:贪心
思路:题目有点难懂,
- 字符串划分为尽可能多的片段,也就是划分后的数组个数尽可能多。
- 同一字母最多出现在一个片段中,也就是相同字母要放在一起。也可以理解为划分后的没有交集。
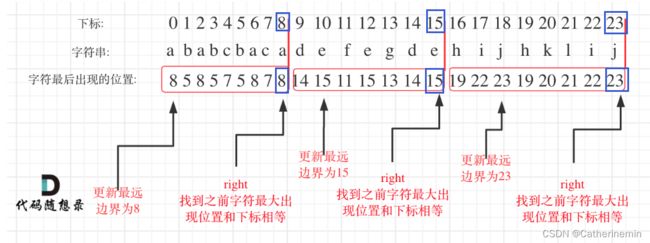
以s = "ababcbacadefegdehijhklij"为例
步骤:
- 通过
字母-‘a’获取索引,存入数组edge中。此时,edge = [8, 5, 7, 14, 15, 11, 13, 19, 22, 23, 20, 21, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]。具体来说,edge[0]表示字母a最后一次出现的索引。0表示没有出现这个字母。 - 遍历chars数组,每次要划分的索引,是max(idx,edge[char[i]-‘a’]),知道
索引==idx,就是找到了切割的点,这个条件还挺难找的。 - 通过
当前的索引-last获取切分的长度
复杂度分析:
- 时间复杂度:O(n)
- 空间复杂度:O(n)
import java.util.LinkedList;
import java.util.List;
class Solution {
public List<Integer> partitionLabels(String S) {
List<Integer> list = new LinkedList<>();
int[] edge = new int[26]; //
char[] chars = S.toCharArray(); // 转为数组
for (int i = 0; i < chars.length; i++) {
edge[chars[i] - 'a'] = i; // 存放字母a-z在数组chars中最后出现的位置,也就是最后出现的索引
}
int idx = 0;
int last = -1;
for (int i = 0; i < chars.length; i++) {
idx = Math.max(idx,edge[chars[i] - 'a']);
if (i == idx) {
list.add(i - last);
last = i;
}
}
return list;
}
public static void main(String[] args) {
Solution solution = new Solution();
solution.partitionLabels("ababcbacadefegdehijhklij");
}
}
56. 合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
教程:https://programmercarl.com/0056.%E5%90%88%E5%B9%B6%E5%8C%BA%E9%97%B4.html
方法一:贪心
思路:
以intervals = [[1,3],[2,6],[8,10],[15,18]]为例子
步骤
- 排序后:
intervals = [[1,3],[2,6],[8,10],[15,18]] - 遍历intervals ,如果
左边界大于最大右边界,就添加到结果中,此时没有交集,直接加入结果,更新左边界和右边界;否则,合并和的区间就是[上一个区间的左边界,下一个区间的右边界],更新右边界 - 遍历完还要添加到结果
细节方面不是很懂,更新边界值那里。
复杂度分析:
- 时间复杂度:O(nlogn)
- 空间复杂度:O(logn)
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
class Solution {
public int[][] merge(int[][] intervals) {
List<int[]> res = new LinkedList<>();
//按照左边界排序
Arrays.sort(intervals, (x, y) -> Integer.compare(x[0], y[0]));
//initial start 是最小左边界
int start = intervals[0][0];
int rightmostRightBound = intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
//如果左边界大于最大右边界
if (intervals[i][0] > rightmostRightBound) {
//加入区间 并且更新start
res.add(new int[]{start, rightmostRightBound});
start = intervals[i][0];
rightmostRightBound = intervals[i][1];
} else {
//更新最大右边界
rightmostRightBound = Math.max(rightmostRightBound, intervals[i][1]);
}
}
res.add(new int[]{start, rightmostRightBound});
return res.toArray(new int[res.size()][]);
}
public static void main(String[] args) {
Solution solution = new Solution();
solution.merge(new int[][] {{1,3},{2,6},{8,10},{15,18}});
}
}