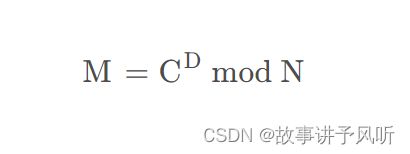对称与非对称加密（DES&RSA）

对称加密是指使用同一个密钥进行信息的加密和解密，加密和解密的过程都使用相同的密钥，因此也称为共享密钥加密。这种加密方式的优点是速度快，适合加密大量的数据，但缺点是密钥需要在通信的双方之间共享。若密钥被泄漏，则整个加密系统的安全性就会被破解。

非对称加密是指使用一对密钥，即公钥和私钥，进行信息的加解密。公钥可以任意发布，不需要保密，而私钥则必须严格保密。加密和解密的过程使用不同的密钥，因此也称为公开密钥加密。这种加密方式的优点是密钥不需要在通信的双方之间共享，安全性较高，但缺点是加解密速度较慢，适合加密少量的数据。

综合来说，对称加密和非对称加密各有其优点和缺点，可以根据不同的需求和场景来选择合适的加密方式。对称加密适用于数据传输量较大的场景，而非对称加密则对安全性要求较高的场景更为适用。实际应用中也常常将对称加密和非对称加密两种方式结合起来使用，以利用各自的优点，提高信息加密的安全性和效率。

一、数据加密标准DES

在DES算法中使用的密钥位64位，其中有效的密钥长度其实只有56位（分成8块每块长为8位，每隔8位设置左后一位为校验位，采用就奇偶校验法）。

DES的加密思想是对密钥和明文都进行一系列复杂变换处理，中间分为多个小段单独异或加密，最后再合成变换得到最终密文，在DES算法中加密的明文较长，需要对DES加密进行16轮的函数循环迭代。

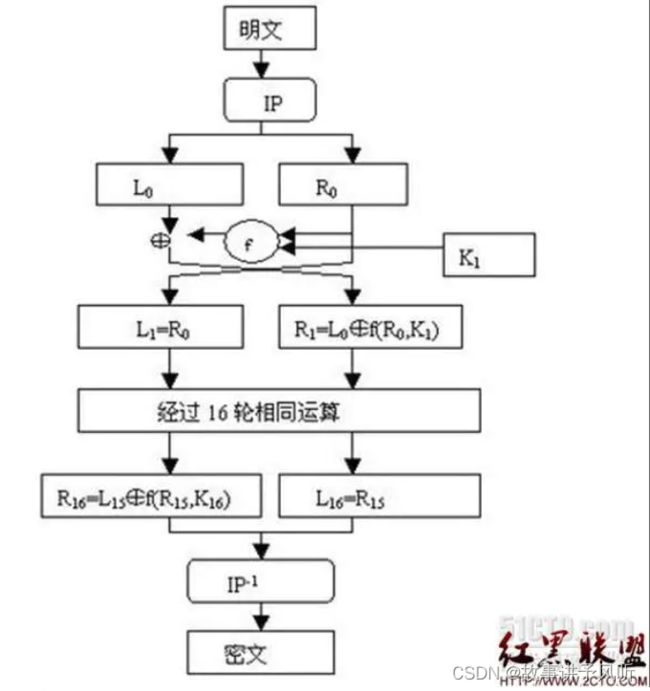
明文的加密整体过程

加密过程如下：

1. 将明文分成64位大小的块，对每个块进行初始置换（IP置换），得到置换后的明文。

2. 将置换后的明文分成左右两部分，每一部分32位。

3. 根据DES算法的规则，对左右两部分分别进行16轮加密。其中每轮加密分为四个步骤：

    (1) 将右半部分进行扩展置换，扩展成48位的数据。

    (2) 将扩展后的数据与密钥进行异或操作，得到的结果为48位的数据。

    (3) 将异或后的结果分成8个6位的数据块，分别通过S盒进行替换。

    (4) 将经过S盒替换后的8个6位数据块组合起来，得到32位的数据。将这个数据进行P盒置换，得到加密后的右半部分。

目的是在加密数据的过程中制造一些雪崩效应。

使用数据块中的1位，将在下一步操作中影响更多位，从而产生扩散效果。

4. 将左右两部分进行交换，以便下一轮加密。

5. 经过16轮加密后，将左部分和右部分进行合并。

6. 将合并后的数据进行逆置换（IP逆置换），得到加密后的密文。

解密过程和加密过程类似，但密钥需要倒序使用，即第一轮的密钥是最后一轮加密时使用的密钥，第二轮的密钥是倒数第二轮加密时使用的密钥，以此类推。

E盒扩展

E盒扩展使用的置换表是固定不变的，包含了32位的原始数据和16个8位扩展数据，它的作用是将原始的32位输入扩展成48位，以进行下一轮的加/解密。

E盒扩展的过程如下：

1. 将32位输入数据分成4段，每段8位。

2. 按照置换表进行扩展，将每个8位输入数据扩展为6位的数据。

3. 扩展后得到的48位数据则作为接下来的DES算法所使用的48位密钥。

S盒压缩

S盒（Substitution box）是DES算法中用于将6位数据块映射到4位数据块的一个固定置换表。S盒将一个6位的数据块替换为一个4位的数据块，共存在8个S盒，每个S盒有64种不同的输入输出映射方式。S盒的作用是将输入的数据块与密钥进行混淆，以增强DES算法的安全性。

S盒压缩的步骤如下：

1. 将第1个S盒的输出的4位数据块作为32位输出数据块的高4位。

2. 将第2个S盒的输出的4位数据块左移4位，与第1个S盒输出的4位数据块合并成一个8位数据块，作为32位输出数据块的下一个4位。

3. 重复上述步骤，将第3个至第8个S盒的输出的4位数据块依次合并到32位输出数据块中。

4. 最终得到的32位数据即为S盒压缩后的结果。

P盒置换

 P盒（Permutation box）是DES算法中用于将32位数据块的位顺序重新排列的一个固定置换表，用于混淆前一轮输出的数据块。P盒置换的过程是将32位数据按照P盒置换表的规则进行重新排列，得到一个新的32位数据块。

P盒置换过程如下：

1. 将置换前的32位数据分成8个组，每个组包含4位。

2. 对每个组内的4位数据，按照P盒置换表的顺序进行排列，排列后得到一个新的4位数据。

3. 将8个新的4位数据按顺序合并起来，即可得到P盒置换后的32位数据。

二、RSA算法

1. 生成公钥和私钥

（1）随意选择两个大的素数P和Q，P不等于Q；

（2）令 N = P × Q 、 T = ( P − 1 ) × ( Q − 1 ) N = P \times Q、T = (P - 1) \times (Q - 1)N=P×Q、T=(P−1)×(Q−1)；

（3）选择一个整数E作为秘钥，需要满足：gcd(E, T)=1 && E

（4）根据 ( D × E )   m o d   T = 1 (D \times E) \ mod \ T = 1(D×E) mod T=1，计算出D，作为另一个秘钥；

（5）使用PK=(N、E)作为公钥、SK=(N, D)作为私钥（当然可以反过来）。

2. 使用公钥加密信息

使用PK=(N、E)公钥加密信息。

若明文为M，则密文C可以按照如下计算得到（要求M

                                       

3. 使用私钥解密信息

使用SK=(N, D)私钥解密信息。

如密文为C，则明文M可以按照如下计算得到：

                                   

4. 例子

以下是一个RSA加密的示例：

1. 选择两个质数p=17和q=11，计算n=pq=187。

2. 计算(p-1)(q-1)=160，选择一个整数e=7，满足gcd(e, 160)=1。

3. 使用扩展欧几里得算法计算e的模反元素d=23，使得7d mod 160=1。

4. 公钥是(n=187, e=7)，私钥是(n=187, d=23)。

5. 加密者选择明文M=88，将其编码成整数m=88。

6. 加密者使用公钥(n=187, e=7)将m加密成密文C，C = 88^7 mod 187 = 27。

7. 解密者使用私钥(n=187, d=23)将密文C解密为明文m，m=C^23 mod 187=88。

这样，明文M=88就被RSA加密算法加密成了密文C=27，再使用私钥解密后可得到原文M=88，实现了加密解密过程。

5. RSA的应用：数字签名

数字签名是实现安全交易的核心技术之一，实现基础是RSA加密技术。

数字签名类似于我们生活中的手写签名，必须保证签名的人事后不能抵赖，同时不能让别人伪造我们的签名。因此数字签名需要保证：

（1）发送者事后不能抵赖对报文的签名；

（2）接受者不能伪造对报文的签名。

如果A向B发送报文M，A手中有私钥，公钥是公开的，A给M使用私钥进行加密再发给B即可。

这样即可保证上述两点：

（1）因为只有A可以对M使用私钥进行加密，A不能抵赖；

（2）B用公钥可以得到原始信息M，如果伪造成M'，则A可以证明其伪造了信息。

6. RSA的安全性

RSA算法的安全性依赖于大数分解。因此为了保证安全性，需要使得P、Q非常大。

因为数据很大，又牵涉到幂次运算，因此计算量很大。

欧拉函数

任意给定正整数n,计算在小于等于n的正整数之中，有多少个与n构成互质关系。计算这个值的方法叫做欧拉函数。以φ(n)表示。如φ(8)=4，应为在1到8之中，与8形成互质关系的有1，3，5，7。

φ(n)的计算方法并不复杂，我们就分情况分析。

第一种情况：

如果n=1，则φ(1)=1。应为1与任何(包括自己)都构成互质关系。

第二种情况：

如果n是质数，则φ(n)=n-1。应为质数与每个小于他的数都构成互质关系。

第三种情况：

如果n是质数的某一个次方，即n=p^k(p为质数，k>=1),则

如φ(8)=φ(2^3)=2^3-2^2=4。

这是应为只有当一个数不包含质数p时，才能与n互质。而包含质数p的数一共有p^(k-1)个，即是1*p、2*p、...、p^(k-1)*p。

上面的式子还可以写成：

第四种情况：

n可以分解成两个互质的整数之积。n = p1 * p2

则 φ(n)=φ(p1p2)=φ(p1)φ(p2)

即积的欧拉函数等于各个因子的欧拉函数之积。如：φ(56)=φ(7*8)=φ(7)*φ(8)=6*4=24

第五种情况：

因为任意大于1的整数，都可以写成一系列质数的积。

根据第四条结论

在根据第三条结论

也就等于

比如：

φ(1323)=φ(3^2*7^2)=1323(1-1/3)(1-1/7)=756

欧拉定理

欧拉定理是指：如果两个正整数a和n互质，则n的欧拉函数φ(n)可以让下面的式子成立：

即是a的φ(n)次方减去1，被n整除。比如，3和7互质，φ(7)=6，(3^6-1)/7=104

如果正整数a与质数p互质，应为φ(p)=p-1，所以欧拉函数可写成：

这个就是著名的费马小定理。

模反元素

如果两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除。

比如：3和11互质，那么3的模反元素是4，应为3*4-1 可以被11整除。4加减11的整数倍数都是3的模反元素。

欧拉定理可以用来证明模反元素必然存在：

可以看到，a的φ(n)-1次方，就是a的模反元素