粒子群算法PSO优化BP神经网络(PSO-BP)回归预测-Matlab代码实现

一、粒子群算法PSO（代码获取：评论区或者私信获取）

        粒子群优化算法（Particle swarm optimization，PSO）是由Kennedy等人于1995年提出的一种经典的启发式算法。PSO受启发于对鸟群捕食行为的研究，是通过群体中的个体之间的协作和信息共享，使得群体位置在解空间中从无序到有序，群体成员通过学习自己和其他成员的经验，不断改变搜索模式，从而寻得最优解。PSO由于具有调整参数少、收敛速度快的优势，目前被广泛应用于神经网络训练优化及其他函数优化等领域。

        PSO算法的基本思想是通过粒子来模拟鸟群中的个体，这些粒子都具备速度和位置属性。粒子群中的每个粒子在自己的搜索空间内单独的寻找最优解，并与其它粒子进行信息共享从而找到当前全局最优解，各个粒子再根据当前全局最优解调整速度和位置，不断迭代更新，从而获取全局最优解。PSO算法的实现步骤为：

（1）初始化最大迭代次数、种群大小、个体学习因子、社会学习因子、惯性权重等参数，初始化粒子群位置，计算初始粒子适应度获得初始最优粒子；

（2）计算种群适应度，更新当前粒子群最优粒子的位置；

（3）更新迄今全局最优粒子的位置和适应度；

（4）循环步骤（2）~（3），直至获得最优个体位置与最优适应度，跳出循环。经过有限次迭代后，粒子群中的每个粒子都会向着最优解靠近。

二、PSO-BP预测模型建

        在BP神经网络的建立过程中，连接权重的随机设置会导致预测结果存在误差，并且梯度下降训练存在速度慢和局部极小值的缺点，对神经网络的训练较难达到全局最优。利用粒子群优化算法PSO对其进行寻优，提高预测精度和泛化能力。构建流程为：

（1）数据归一化，建立BP神经网络，确定拓扑结构并初始化网络的权值和阈值；

（2）初始化PSO参数，最大迭代次数、种群大小、个体学习因子、社会学习因子、惯性权重等参数；

（3）初始化PSO的种群位置，根据BP神经网络结构，计算出需要优化的变量元素个数；

（4）PSO优化，适应度函数设置为BP网络预测的均方误差，循环PSO优化过程，不断更新最优粒子的位置直至最大迭代次数，终止PSO算法；

（5）PSO算法优化后的最优权值阈值参数赋予BP神经网络，即输出最优的PSO-BP模型，利用PSO-BP进行训练和预测并与优化前的BP网络进行对比分析。 

三、关键代码

%% 建立BP模型
net=newff(inputn,outputn,hiddennum_best,{'tansig','purelin'},'trainlm');
 
% 设置BP参数
net.trainParam.epochs=1000;        % 训练次数
net.trainParam.lr=0.01;            % 学习速率
net.trainParam.goal=0.00001;       % 训练目标最小误差
net.trainParam.show=25;            % 显示频率
net.trainParam.mc=0.01;            % 动量因子
net.trainParam.min_grad=1e-6;      % 最小性能梯度
net.trainParam.max_fail=6;         % 最高失败次数

%% 初始化PSO参数
popsize=10;   %初始种群规模
maxgen=50;   %最大进化代数
dim=inputnum*hiddennum_best+hiddennum_best*hiddennum_best+hiddennum_best+hiddennum_best*outputnum+outputnum;    %自变量个数
lb=repmat(-3,1,dim);    %自变量下限
ub=repmat(3,1,dim);   %自变量上限
c1 = 2;  % 每个粒子的个体学习因子，也称为个体加速常数
c2 = 2;  % 每个粒子的社会学习因子，也称为社会加速常数
w = 0.9;  % 惯性权重
vmax =3*ones(1,dim); % 粒子的最大速度
vmax=repmat(vmax,popsize,1);

%% 初始化粒子的位置和速度
x = zeros(popsize,dim);
for i = 1: dim
    x(:,i) = lb(i) + (ub(i)-lb(i))*rand(popsize,1);   % 随机初始化粒子所在的位置在定义域内
end
v = -vmax + 2*vmax .* rand(popsize,dim);  % 随机初始化粒子的速度

%% 计算适应度
fit = zeros(popsize,1);  % 初始化这n个粒子的适应度全为0
for i = 1:popsize  % 循环整个粒子群，计算每一个粒子的适应度
    [fit(i),NET]= fitness(x(i,:),inputnum,hiddennum_best,outputnum,net,inputn,outputn,output_train,inputn_test,outputps,output_test);   % 调用函数来计算适应度
    eval( strcat('NETA.net',int2str(i),'=NET;'))
end 
pbest = x;   % 初始化这n个粒子迄今为止找到的最佳位置
ind = find(fit == min(fit), 1);  % 找到适应度最小的那个粒子的下标
gbest = x(ind,:);  % 定义所有粒子迄今为止找到的最佳位置
fit_gbest=fit(ind);  
eval( strcat('Net=NETA.net',int2str(ind ),';'));
eval( strcat('NETT=NETA.net',int2str(ind),';'));

%% 进化过程
for d = 1:maxgen  % 开始迭代，一共迭代K次
    for i = 1:popsize   % 依次更新第i个粒子的速度与位置
        v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));  % 更新第i个粒子的速度
        for j = 1: dim
            if v(i,j) < -vmax(j)
                v(i,j) = -vmax(j);
            elseif v(i,j) > vmax(j)
                v(i,j) = vmax(j);
            end
        end
        x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
        for j = 1: dim
            if x(i,j) < lb(j)
                x(i,j) = lb(j);
            elseif x(i,j) > ub(j)
                x(i,j) = ub(j);
            end
        end
        [fit(i),NET] = fitness(x(i,:),inputnum,hiddennum_best,outputnum,net,inputn,outputn,output_train,inputn_test,outputps,output_test); 
        eval( strcat('NETA.net',int2str(i),'=NET;'))      [fit_pbest,~]=fitness(pbest(i,:),inputnum,hiddennum_best,outputnum,net,inputn,outputn,output_train,inputn_test,outputps,output_test);
        if fit(i) 

四、仿真结果

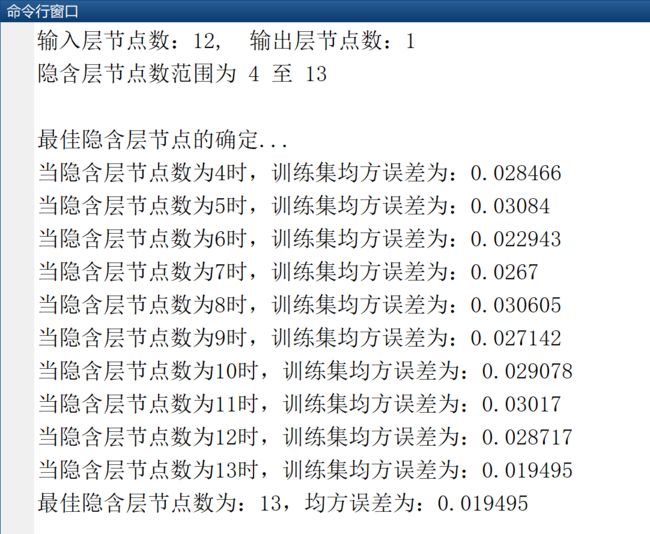
（1）根据经验公式，通过输入输出节点数量，求得最佳隐含层节点数量：

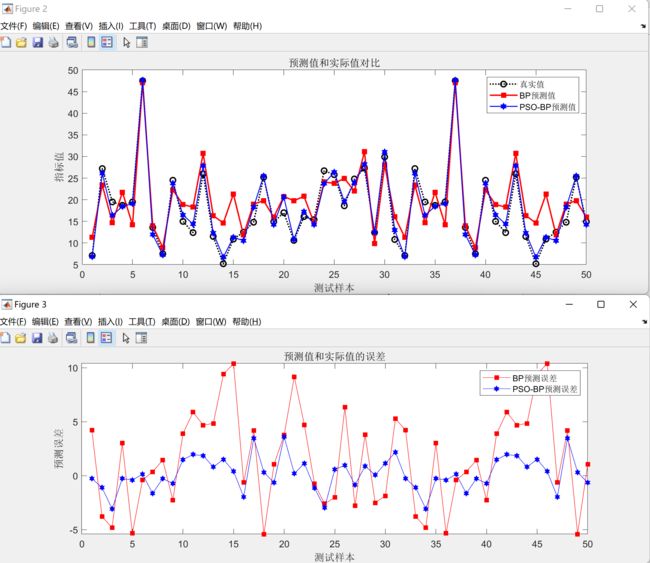
（2）PSO-BP和BP的预测对比图和误差图

  （3）BP和PSO-BP的各项误差指标，预测准确率

 （4）粒子群算法PSO适应度进化曲线

  （5）BP和PSO-BP模型的回归图

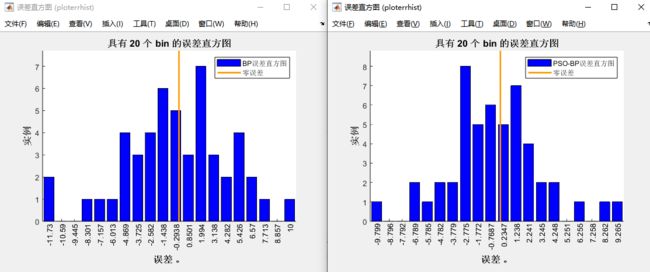
  （6）BP和PSO-BP模型的误差直方图

五、BP算法优化

BP算法优化
遗传算法  GA-BP	灰狼算法  GWO-BP
鲸鱼算法  WOA-BP	粒子群算法  PSO-BP
麻雀算法  SSA-BP	布谷鸟算法  CS-BP