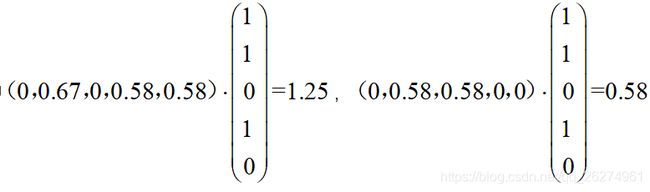协同过滤算法—推荐系统基础算法（含python代码实现以及详细例子讲解）

一、 算法简介

1.1 算法概述

协同过滤（Collaborative Filtering，简写CF）简单来说就是根据已有数据来推测未知的数据的一种算法。在推荐系统中协同过滤算法一般是指在海量用户中发掘一小部分和你品味比较类似的，在协同过滤中，这些用户成为你的邻居，从而基于这些邻居的信息为你推荐商品。基于启发式的协同过滤算法可以分为基于用户的协同过滤算法（User-Based）和基于物品的协同过滤算法（Item-Based）。

1.2 算法核心和步骤

协同过滤算法核心步骤如下：
1）收集用户偏好；
2）找到相似的用户或物品；
3）计算并推荐。

二、基于用户的协同过滤算法（User-Based）

2.1 相似度及预测值的计算

2.1.1 相似度计算

在协同过滤中，一个重要的环节就是如何选择合适的相似度计算方法，常用的相似度计算方法包括皮尔逊相关系数等。
皮尔逊相关系数的计算公式如下所示：

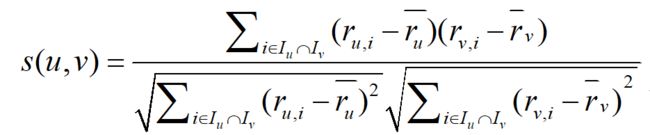
其中，i 表示项，例如商品；$I_u$ 表示用户 u 评价的项集；$I_v$ 表示用户 v 评价的项集；$r_{u，i}$ 表示用户 u 对项 i 的评分；$r_{v，i}$ 表示用户 v 对项 i 的评分； $\overline{r_u}$表示用户 u 的平均评分； $\overline{r_v}$表示用户 v 的平均评分。

2.1.2 预测值的计算

另一个重要的环节就是计算用户 u 对未评分商品的预测分值。首先根据上一步中的相
似度计算，寻找用户 u 的邻居集 N∈U，其中 N 表示邻居集，U 表示用户集。 然后，结合用户评分数据集，预测用户 u 对项 i 的评分，计算公式如下所示：

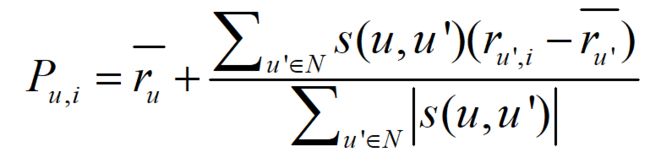
预测用户 u 对项 i 的评分
其中，s（u，u’）表示用户 u 和用户 u’的相似度。

2.2 通过例子理解

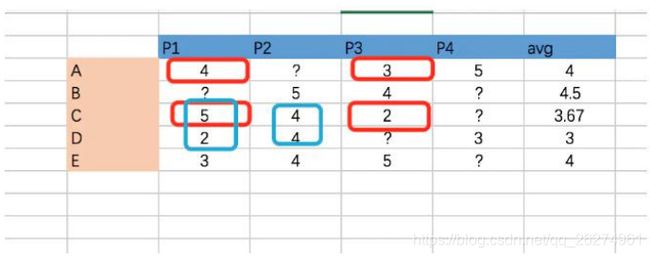
假设有如下电子商务评分数据集，预测用户 C 对商品 4 的评分。
表3-1 电子商务评分数据集

用户	商品1	商品2	商品3	商品4
用户A	4	？	3	5
用户B	？	5	4	？
用户C	5	4	2	？
用户D	2	4	？	3
用户E	3	4	5	？

表中 ？表示评分未知。根据基于用户的协同过滤算法步骤，计算用户 C 对商品 4 的评分，其步骤如下所示。
（1）寻找用户 C 的邻居 从数据集中可以发现，只有用户 A 和用户 D 对商品 4 评过分数，因此候选邻居只有 2 个，分别为用户 A 和用户 D。用户 A 的平均评分为 4，用户 C 的平均评分为 3.667，用户 D 的平均评分为 3。

（2）根据皮尔逊相关系数公式计算与用户C相关用户的相似度
红色区域计算 C 用户与 A 用户，则用户 C 和用户 A 的相似度为：
用户 C 与用户 A 的相似度
蓝色区域计算 C 用户与 D 用户，则用户 C 和用户 D 的相似度为:
用户 C 与用户 D 的相似度
（3）预测用户 C 对商品 4 的评分 根据上述评分预测公式，计算用户 C 对商品 4 的评分，如下所示： 用户 C 对商品 4 的评分为：
依此类推，可以计算出其他未知的评分。
结论：通过计算，可得s(M,N)=s(N,M)(其中M,N为用户名)

通过得到的预测值可以补全未知数据，如图表4-1所示
表4-1 电子商务评分数据集

用户	商品1	商品2	商品3	商品4
用户A	4	4.305	3	5
用户B	4.730	5	4	5
用户C	5	4	2	4.272
用户D	2	4	3.481	3
用户E	3	4	5	4.000

2.4 python代码实现

这个代码是对上面例子的实现

'''
基于用户的推荐算法
'''
from math import sqrt,pow
import operator
class UserCf():

    #获得初始化数据,计算每个用户的评分的平均值
    def __init__(self,data):
        self.data=data
        self.ave = {}
        self.max = 0
        for key,value in self.data.items():
            sum1 = 0.0
            for item,score in value.items():
                if(int(item)>self.max):
                    self.max = int(item)
                sum1 += score
            self.ave[key] = sum1/len(data[key])

        #1.获取用户待预测分数的相关用户，如找到用户C中待评分商品4的预测分数相关用户A，D
    def find_user(self,item_goal):
        user_goal = []
        for key,values in self.data.items():
            for key1,value1 in values.items():
                if(key1 == item_goal):
                    user_goal.append(key)
                    break
        return user_goal

    #2.计算待预测分数中相关用户中两个用户之间的皮尔逊相关系数
    def pearson(self,user1,item_goal):#数据格式为：商品，评分  A:{'a': 4.0, 'c': 3.0, 'd': 5.0
        user_goal = self.find_user(item_goal)
        denominator1 = 0.0 #分母1--待预测用户的分母1
        denominator2 = 0.0 #分母2--相关用户的分母2
        molecule = 0.0     #分子
        r = {}             #皮尔逊系数字典
        try:
            for user2 in user_goal:
                for item_, score_ in self.data[user2].items():
                    for item1,score1 in self.data[user1].items():
                        if(item_ == item1):
                            molecule += (float(score_)-self.ave[user2])*(float(score1)-self.ave[user1])
                            denominator1 += pow(float(score1)-self.ave[user1],2)
                            denominator2 += pow(float(score_)-self.ave[user2],2)
                r.setdefault(user1, {})
                r[user1].setdefault(user2,0)
                r[user1][user2] = (molecule)/sqrt(denominator1*denominator2)
                molecule = 0.0
                denominator1 = 0.0
                denominator2 = 0.0
        except e:
            print("异常信息:",e.message)
            return None
        return r#返回相关用户的皮尔逊系数

    #3.根据皮尔逊系数预测评分
    def prediction(self,user1, item_goal):
        ave1 = self.ave[user1]
        r = self.pearson(user1,item_goal)
        user_goal = self.find_user(item_goal)
        anw1 = 0.0
        anw2 = 0.0
        for user in user_goal:
            anw1 += r[user1][user]*((self.data[user][item_goal])-(self.ave[user]))
            anw2 += abs(r[user1][user])
        predict = ave1 + anw1/anw2
        self.data[user1][item_goal] = round(predict,2)

    #扫描数据集，收集未填充数据
    def scan(self):
        item_map = [str(i) for i in range(1,self.max+1)]
        for user,value in self.data.items():
            item_list = []
            for m,n in value.items():
                item_list.append(m)
            for item in item_map:
                if(item not in item_list):
                    self.prediction(user,item)
        for user, value in self.data.items():
            self.data[user] = sorted(self.data[user].items(),key = lambda d:d[0])
        return self.data

if __name__=='__main__':
    users = {'A': {'1': 4.0, '3': 3.0, '4': 5.0},
             'B': {'2': 5.0, '3': 4.0},
             'C': {'1': 5.0, '2': 4.0,'3': 2.0},
             'D': {'1': 2.0, '2': 4.0,'4': 3.0},
             'E': {'1': 3.0, '2': 4.0,'3': 5.0},
             }
    userCf=UserCf(data=users)
    recommandList=userCf.scan()
    print("协同过滤后的评分矩阵")
    for key,value in recommandList.items():
        print(key,value)

本算法采用简单的皮尔逊相关系数实现协同过滤

#!/usr/bin/python
#基于用户的推荐算法
from math import sqrt,pow
import operator
class UserCf():

    #获得初始化数据
    def __init__(self,data):
        self.data=data;

    #通过用户名获得电影列表，仅调试使用
    def getItems(self,username1,username2):
        return self.data[username1],self.data[username2]

    #计算两个用户的皮尔逊相关系数
    def pearson(self,user1,user2):#数据格式为：电影，评分  {'Snakes on a Plane': 4.5, 'You, Me and Dupree': 1.0, 'Superman Returns': 4.0}
        sumXY=0.0;
        n=0;
        sumX=0.0;
        sumY=0.0;
        sumX2=0.0;
        sumY2=0.0;
        try:
            for movie1,score1 in user1.items():
                if movie1 in user2.keys():#计算公共的电影的评分
                    n+=1;
                    sumXY+=score1*user2[movie1]
                    sumX+=score1;
                    sumY+=user2[movie1]
                    sumX2+=pow(score1,2)
                    sumY2+=pow(user2[movie1],2)

            molecule=sumXY-(sumX*sumY)/n;
            denominator=sqrt((sumX2-pow(sumX,2)/n)*(sumY2-pow(sumY,2)/n))
            r=molecule/denominator
        except Exception,e:
            print "异常信息:",e.message
            return None
        return r

    #计算与当前用户的距离，获得最临近的用户
    def nearstUser(self,username,n=1):
        distances={};#用户，相似度
        for otherUser,items in self.data.items():#遍历整个数据集
            if otherUser not in username:#非当前的用户
                distance=self.pearson(self.data[username],self.data[otherUser])#计算两个用户的相似度
                distances[otherUser]=distance
        sortedDistance=sorted(distances.items(),key=operator.itemgetter(1),reverse=True);#最相似的N个用户
        print "排序后的用户为：",sortedDistance
        return sortedDistance[:n]


    #给用户推荐电影
    def recomand(self,username,n=1):
        recommand={};#待推荐的电影
        for user,score in dict(self.nearstUser(username,n)).items():#最相近的n个用户
            print "推荐的用户：",(user,score)
            for movies,scores in self.data[user].items():#推荐的用户的电影列表
                if movies not in self.data[username].keys():#当前username没有看过
                    print "%s为该用户推荐的电影：%s"%(user,movies)
                    if movies not in recommand.keys():#添加到推荐列表中
                        recommand[movies]=scores

        return sorted(recommand.items(),key=operator.itemgetter(1),reverse=True);#对推荐的结果按照电影评分排序

if __name__=='__main__':
    users = {'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5,'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5,'The Night Listener': 3.0},

             'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5,'Just My Luck': 1.5, 'Superman Returns': 5.0, 'The Night Listener': 3.0,'You, Me and Dupree': 3.5},

             'Michael Phillips': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.0,'Superman Returns': 3.5, 'The Night Listener': 4.0},

             'Claudia Puig': {'Snakes on a Plane': 3.5, 'Just My Luck': 3.0,'The Night Listener': 4.5, 'Superman Returns': 4.0,'You, Me and Dupree': 2.5},

             'Mick LaSalle': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,'Just My Luck': 2.0, 'Superman Returns': 3.0, 'The Night Listener': 3.0,'You, Me and Dupree': 2.0},

             'Jack Matthews': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,'The Night Listener': 3.0, 'Superman Returns': 5.0, 'You, Me and Dupree': 3.5},

             'Toby': {'Snakes on a Plane': 4.5, 'You, Me and Dupree': 1.0, 'Superman Returns': 4.0}
             }

    userCf=UserCf(data=users)
    recommandList=userCf.recomand('Toby', 2)
    print("最终推荐：%s"%recommandList)

原文链接：https://blog.csdn.net/wickedvalley/article/details/80095007

三、基于物品的协同过滤算法（Item-Based）

基于物品的协同过滤算法通过计算不同用户对不同物品的评分获得物品间的关系，基于物品间的关系对用户进行相似物品的推荐，评分即代表用户对物品的态度和偏好。比如，用户A同时购买了物品x，y，那么说明x，y之间的相关度高，当用户B也购买了物品x时，那么可以预测B也可能买物品y。
可以看出基于用户的协同过滤是计算用户间的相似度，而基于物品的协同过滤算法是计算物品间的相似度，进而产生推荐

3.1 算法流程：

1）根据用户与物品的喜好矩阵，构建用户–>物品的倒排（即倒查表）；
2）构建物品与物品的共现矩阵；
3）计算物品之间的相似度，即计算相似矩阵；
4）根据用户的历史记录，给用户推荐物品。
（其中，2、3步实际上可以合为一步，相似矩阵为共现矩阵的改进优化。）
注：该算法也适合解决基于用户的协同过滤问题

3.2 实例

如下表，行表示用户，列表示物品，1 表示用户喜欢该物品，？表示用户是否喜欢该商品未知。
表1

用户\商品	商品a	商品b	商品c	商品d	商品e
用户A	1	1	？	1	1
用户B	？	1	1	？	1
用户C	？	？	1	1	？
用户D	？	1	1	1	？
用户E	1	？	？	1	？

3.2.1 构建用户—>物品的倒排

A ： a 、 b 、 d
B ： b 、 c 、 e
C ： c 、 d
D ： b 、 c 、 d
E ： a 、 d

3.2.2 构建物品与物品的共现矩阵

共现矩阵表示同时喜欢两个物品的用户数，是一个对称矩阵，是由用户—>物品的倒排表计算出来的。

商品	a	b	c	d	e
a	-	1	0	2	0
b	1	-	2	2	1
c	0	2	-	2	1
d	2	2	2	-	0
e	0	1	1	0	-

3.2.3 计算物品之间的相似度，即计算相似矩阵

设|N(i)| 表示喜欢物品的用户数，|N(i)∩N(j)| 表示同时喜欢物品i、j用户数，则物品i与物品j的相似度为：

但上式有一个问题，当物品j是一个很热门的物品时，人人都喜欢，那么wij就会很接近 1 ，那上式会让很多物品都和热门物品有一个很大的相似度。所以，需要改进一下公式：

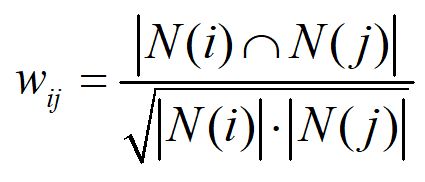
上式中，分子即为共现矩阵，矩阵 N（用于计算分母）表示喜欢某物品的用户数（是总的用户数）.

矩阵N如下：

物品	a	b	c	d	e
用户数	2	3	3	4	1

所以，物品之间的余弦相似矩阵如下（可以看到该相似度矩阵也是对阵的 ）：

3.2.4 根据用户的历史记录，给用户推荐物品

基于用户的推荐算法思路：
推荐的结果 = 改进的共现矩阵 * 评分矩阵 = 相似矩阵 * 评分矩阵
ItemCF 通过如下公式计算用户 u 对一个物品 j的兴趣度：

上式的含义是：和用户历史上感兴趣的物品越相似的物品，越有可能在用户的推荐列表中获得比较高的排名。
如：以用户 A 为例，建立用户对物品的评分矩阵（即 A对物品的兴趣度）如下：

商品	评分
a	1
b	1
c	0
d	1
e	0

用户 A 已经见过物品 a , b , d并对其进行了评分，所以我们需要选择是推荐物品c还是物品e给用户 A
推荐结果：

商品	兴趣度
c	1.25
e	0.58

根据之前的协同过滤算法可得结果，如表所示：
协同过滤算法结果

商品	a	b	c	d	e
a	-	0.41	0	0.71	0
b	0.41	-	0.67	0.58	0.58
c	0	0.67	-	0.58	0.58
d	0.71	0.58	0.58	-	0
e	0	0.58	0.58	0	-

其中对商品c与商品e的预测为 ：

则可以看出，通过计算项目与其他项目的相似度和带预测用户对项目的喜爱度的点积，可以计算出用户 A 对物品 c 的预测兴趣度（即喜爱程度）为1.25， 对物品 e 的预测兴趣度（即喜爱程度）为0.58。所以，可向 A推荐物品 c .

3.3 python 代码实现

```python
#/python/Item_CF.py
from math import sqrt
import operator

#1.构建用户-->物品的倒排
def loadData(files):
    data ={}
    for line in files:
        user,score,item=line.split(",")
        data.setdefault(user,{})
        data[user][item]=score
    print("----1.用户：物品的倒排----")
    print(data)
    return data

def loadData2(files):
    data={}
    for line in files:
        user,item,score,timestamp=line.split(",")
        data.setdefault(user,{})
        data[user][item]=score
    print("----1.用户：物品的倒排----")
    print(data)
    return data

#2.计算
#2.1 构造物品-->物品的共现矩阵
#2.2 计算物品与物品的相似矩阵
#(这里采用的是余弦相似度算法计算的物品间的相似度)
def similarity(data):
    # 2.1 构造物品：物品的共现矩阵
    N={}#喜欢物品i的总人数
    C={}#喜欢物品i也喜欢物品j的人数
    for user,item in data.items():
        for i,score in item.items():
            N.setdefault(i,0)
            N[i]+=1
            C.setdefault(i,{})
            for j,scores in item.items():
                if j not in i:
                    C[i].setdefault(j,0)
                    C[i][j]+=1
                    
    print("---2.构造的共现矩阵---")
    print ('N:',N)
    print ('C:',C)

    #2.2 计算物品与物品的相似矩阵
    W={}
    for i,item in C.items():
        W.setdefault(i,{})
        for j,item2 in item.items():
            W[i].setdefault(j,0)
            W[i][j]=C[i][j]/sqrt(N[i]*N[j])
            
    print("---3.构造的相似矩阵---")
    print(W)
    return W

#3.根据用户的历史记录，给用户推荐物品
def recommandList(data,W,user,k=3,N=10):
    rank={}
    for i,score in data[user].items():	#获得用户user历史记录，如A用户的历史记录为{'a': '1', 'b': '1', 'd': '1'}
        for j,w in sorted(W[i].items(),key=operator.itemgetter(1),reverse=True)[0:k]:	#获得与物品i相似的k个物品
            if j not in data[user].keys():	#该相似的物品不在用户user的记录里
                rank.setdefault(j,0)
                rank[j]+=float(score) * w
                
    print("---4.推荐----")
    print(sorted(rank.items(),key=operator.itemgetter(1),reverse=True)[0:N])
    return sorted(rank.items(),key=operator.itemgetter(1),reverse=True)[0:N]

if __name__=='__main__':
    # 用户，兴趣度，物品
    # 实例1
    uid_score_bid = ['A,1,a', 'A,1,b', 'A,1,d', 'B,1,b', 'B,1,c', 'B,1,e', 'C,1,c', 'C,1,d', 'D,1,b', 'D,1,c', 'D,1,d',
                     'E,1,a', 'E,1,d']
    data=loadData(uid_score_bid)	#获得数据
    W=similarity(data)	#计算物品相似矩阵
    recommandList(data,W,'A',3,10)	#推荐
    # 实例2
    users2 = []
    fp_2 = open("u.data", "r", encoding='utf-8')
    for line2 in fp_2.readlines():
        line_2=line2.replace("\t",",")
        lines2 = line_2.strip().split("\n")
        users2+=lines2
    data2 = loadData2(users2)  # 获得数据
    W2 = similarity(data2)  # 计算物品相似矩阵
	recommandList(data2, W3, '160', 3, 20)  # 推荐

原文链接：https://blog.csdn.net/qq_42851418/article/details/85265723

四、协同过滤算法总结

4.1 协同过滤算法描述

推荐系统应用数据分析技术，找出用户最可能喜欢的东西推荐给用户，现在很多电子商务网站都有这个应用。目前用的比较多、比较成熟的推荐算法是协同过滤（Collaborative Filtering，简称CF）推荐算法，CF的基本思想是根据用户之前的喜好以及其他兴趣相近的用户的选择来给用户推荐物品。

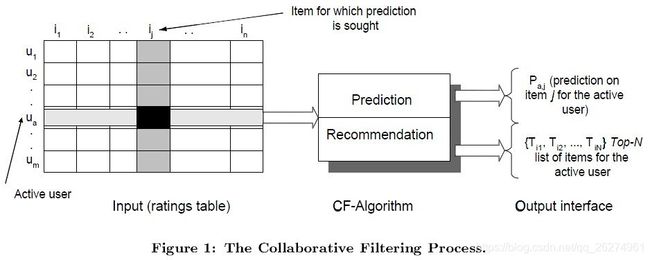
如图所示为协同过滤算法的过程，在CF中，用m×n的矩阵表示用户对物品的喜好情况评价矩阵，一般用打分表示用户对物品的喜好程度，分数越高表示越喜欢这个物品，0表示没有买过该物品。图中行表示一个活跃的用户，列表示一个寻求预测的项目， 表示用户i对物品j的打分情况。
协同过滤算法（CF-Algorithm）分为两个过程，一个为预测过程（Prediction），另一个为推荐过程(Recommendation)。输出接口（Output interface）预测过程是预测用户对没有购买过的物品的可能打分值 (prediction on item j for the active user)，推荐是根据预测阶段的结果推荐用户最可能喜欢的一个或Top-N个物品(Top-N list of items for the active user)。

4.2 User-based与Item-based算法对比

CF算法分为两大类，一类为基于memory的（Memory-based），另一类为基于Model的（Model-based），User-based和Item-based算法均属于Memory-based类型，具体细分类可以参考wikipedia的说明。
User-based的基本思想是如果用户A喜欢物品a，用户B喜欢物品a、b、c，用户C喜欢a和c，那么认为用户A与用户B和C相似，因为他们都喜欢a，而喜欢a的用户同时也喜欢c，所以把c推荐给用户A。该算法用最近邻居（nearest-neighbor）算法找出一个用户的邻居集合，该集合的用户和该用户有相似的喜好，算法根据邻居的偏好对该用户进行预测。
User-based算法存在两个重大问题：

1. 数据稀疏性。一个大型的电子商务推荐系统一般有非常多的物品，用户可能买的其中不到1%的物品，不同用户之间买的物品重叠性较低，导致算法无法找到一个用户的邻居，即偏好相似的用户。
2. 算法扩展性。最近邻居算法的计算量随着用户和物品数量的增加而增加，不适合数据量大的情况使用。

Iterm-based的基本思想是预先根据所有用户的历史偏好数据计算物品之间的相似性，然后把与用户喜欢的物品相类似的物品推荐给用户。还是以之前的例子为例，可以知道物品a和c非常相似，因为喜欢a的用户同时也喜欢c，而用户A喜欢a，所以把c推荐给用户A。
因为物品直接的相似性相对比较固定，所以可以预先在线下计算好不同物品之间的相似度，把结果存在表中，当推荐时进行查表，计算用户可能的打分值，可以同时解决上面两个问题。

原文出处：http://blog.csdn.net/huagong_adu/article/details/7362908

五、参考文章资料来源

1、https://www.bilibili.com/video/BV1WX4y1K7Xj
2、https://blog.csdn.net/m0_51132284/article/details/112793371
3、https://blog.csdn.net/wickedvalley/article/details/80095007
4、https://blog.csdn.net/qq_42851418/article/details/85265723
5、http://blog.csdn.net/huagong_adu/article/details/7362908