CINTA第六次作业

第十章习题

第一题

$运用CRT求解：x\equiv 8(mod11)x\equiv 3(mod19)$

$gcd(11,19)=1,x\equiv (8\ast 19\ast 19^{-1}+3\ast 11\ast 11^{-1})mod11\ast 19$
$19\ast 19^{-1}\equiv 1(mod11),19^{-1}=7$
$11\ast 11^{-1}\equiv 1(mod19),11^{-1}=7$
$x\equiv (8\ast 19\ast 7+3\ast 11\ast 7)mod11\ast 19\equiv 1295(mod209)\equiv 41$
$故,x=41,经验证x=41为同余方程组的解$

---

第二题

$运用CRT求解：x\equiv 1(mod5)x\equiv 2(mod7)$
$x\equiv 3(mod9)x\equiv 4(mod11)$

$5,7,9,11两两互素$
$x\equiv (1\ast (7\ast 9\ast 11)\ast a^{-1}+2\ast (5\ast 9\ast 11)\ast b^{-1}+3\ast (5\ast 7\ast 11)\ast c^{-1}+4\ast (5\ast 7\ast 9)\ast d^{-1})mod(5\ast 7\ast 9\ast 11)$
$(7\ast 9\ast 11)\ast a^{-1}\equiv 1(mod5),a^{-1}=2$
$(5\ast 9\ast 11)\ast b^{-1}\equiv 1(mod7),b^{-1}=3$
$(5\ast 7\ast 11)\ast c^{-1}\equiv 1(mod9),c^{-1}=4$
$(5\ast 7\ast 9)\ast d^{-1}\equiv 1(mod11),d^{-1}=8$
$x\equiv 1\ast 7\ast 9\ast 11\ast 2+2\ast 5\ast 9\ast 11\ast 3+3\ast 5\ast 7\ast 11\ast 4+4\ast 5\ast 9\ast 7\ast 8(mod5\ast 7\ast 9\ast 11)\equiv 1731$
$故,x=1731,经验证x=1731为同余方程组的解$

---

第三题

手动计算$2000^{2019}(mod221)$

$221=13\ast 17,gcd(13,17)=1$
$2000\leftrightarrow (11,11)$
$(11,11{)}^{2019}=([11^{2019}mod13],[11^{2019}mod17])$
$运用费马小定理，11^{2019}mod13\equiv 11^{12\ast 168+3}mod13\equiv 11^{3}mod13\equiv (-8)mod13\equiv 5$
$11^{2019}mod17\equiv 11^{16\ast 126+3}mod17\equiv 11^{3}mod17\equiv (-216)mod17\equiv 5$
$(11,11{)}^{2019}=(5,5)$
$所以，2000^{2019}(mod221)=5$
$PS:2000^{2019}(mod221)不能运用费马小定理，因为221不是素数$

---

第七题

实现一个利用CRT求解同余方程的程序

$运用拓展欧几里得算法求逆元$
$前段时间做极客大挑战2023的密码题，发现了一道拓展中国剩余定理的解法$
$了解了一下，确实exCRT和CRT可以说是没什么关系，思路大致是明白了$

def exgcd(a, b):
    if b == 0:
        return 1, 0, a
    x, y, q = exgcd(b, a % b)
    x, y = y, (x - a // b * y)
    return x, y, q


def CRT(a, n):
    sum = 0
    prod = 1
    for n_i in n:
        prod *= n_i
    for a_i, n_i in zip(a, n):
        p = prod // n_i
        sum += a_i * p * exgcd(p, n_i)[0]
    return int(sum % prod)


def exCRT(a, m, n):     # 模数m，余数a，组数n
    if n == 1:
        if m[0] > a[0]:
            return a[0]
        else:
            return -1
    for i in range(n):
        if m[i] <= a[i]:
            return -1
        x, y, d = exgcd(m[0], m[i])
        if (a[i] - a[0]) % d != 0:
            return -1
        t = m[i] // d
        x = (a[i] - a[0]) // d * x % t
        a[0] = x * m[0] + a[0]
        m[0] = m[0] * m[i] // d
        a[0] = (a[0] % m[0] + m[0]) % m[0]
    return a[0]


# x = a_i mod n_i
a0 = [1, 2, 3, 4]
n0 = [5, 7, 9, 11]
a1 = [1, 1, 4]
n1 = [3, 6, 7]
ans0 = CRT(a0, n0)
ans1 = CRT(a1, n1)
ans2 = exCRT(a0, n0, 4)
ans3 = exCRT(a1, n1, 3)
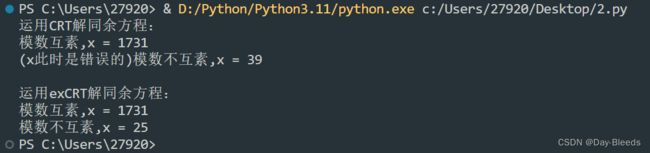
print("运用CRT解同余方程：")
print("模数互素,x =", ans0)
print("(x此时是错误的)模数不互素,x =", ans1)
print("\n运用exCRT解同余方程：")
print("模数互素,x =", ans2)
print("模数不互素,x =", ans3)

---