【二叉树】- 四种遍历方式
本文主要介绍二叉树的四种遍历方式,并实现了四种遍历方式,期间介绍了二叉树以及满二叉树和完全二叉树。
个人简介:一个全栈工程师的升级之路!
个人专栏:数据结构
CSDN主页 发狂的小花
人生秘诀:学习的本质就是极致重复!
目录
1 二叉树
2 完全二叉树和满二叉树
2.1 深度计算
3 二叉树的遍历
3.1 先序遍历
3.2 中序遍历
3.3 后序遍历
3.4 层次遍历
1 二叉树
二叉树是一种特殊的树形结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
二叉树每个节点都有一个值,并且满足从根节点到叶子节点的所有路径上的值都是递增或递减的。根据二叉树的性质,我们还可以知道,二叉树中,第 i 层最多有 ![]() 个结点,如果二叉树的深度为 K,那么此二叉树最多有
个结点,如果二叉树的深度为 K,那么此二叉树最多有 ![]() 个结点。
个结点。
此外,对于二叉树的遍历方式有三种:前序遍历、中序遍历和后序遍历。
前序遍历的顺序是首先访问根结点,然后递归地遍历左子树,最后递归地遍历右子树;
中序遍历的顺序是首先递归地遍历左子树,然后访问根结点,最后递归地遍历右子树;
后序遍历的顺序是首先递归地遍历左子树,然后递归地遍历右子树,最后访问根结点。
2 完全二叉树和满二叉树
满二叉树与完全二叉树是两种相关但具有不同特点的二叉树结构。
满二叉树是指一个二叉树的所有层都完全填满,且每层的节点数均达到最大值。
完全二叉树则是指除最后一层外,其它各层的节点数均达到最大值,最后一层从左向右连续填充。
具体来说,如果设二叉树的深度为h,那么对于满二叉树来说,每一层的结点数都达到了最大值![]() ,即每一层的节点数都是满的;而对于完全二叉树来说,除去最后一层,其它各层的节点数也都达到了最大值,但是最后一层可能并未满。
,即每一层的节点数都是满的;而对于完全二叉树来说,除去最后一层,其它各层的节点数也都达到了最大值,但是最后一层可能并未满。
满二叉树和完全二叉树的主要区别在于:满二叉树的每一层都是满的,即每一层的节点数都达到了最大值;而完全二叉树则是除了最后一层外,其它层都是满的,但最后一层可能不满。
2.1 深度计算
对于有n个节点的满二叉树和完全二叉树:
满二叉树:满二叉树的深度为![]() 。
。
完全二叉树:在完全二叉树中,具有n个结点的完全二叉树深度为![]() ,其中
,其中![]() 是向下取整。
是向下取整。
3 二叉树的遍历
二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有的节点,确保每个节点只被访问一次。
二叉树的遍历方式有以下四种:
(1)先序遍历(根左右)
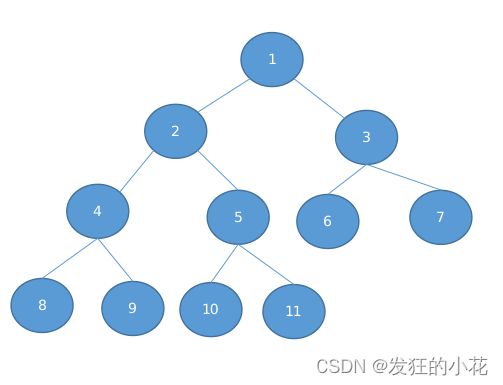
首先访问根结点,然后递归地遍历左子树,最后遍历右子树。例如对于二叉树:1 2 3 4 5 6 7 8 9 10 11,先序遍历的结果为:1->2->4->8->9->5->10->11->3->6->7。
(2)中序遍历(左根右)
首先遍历左子树,然后访问根结点,最后遍历右子树。例如对于二叉树:1 2 3 4 5 6 7 8 9 10 11,中序遍历的结果为:8->4->9->2->10->5->11->1->6->3->7。
(3)后序遍历(左右根)
首先遍历左子树,然后遍历右子树,最后访问根结点。例如对于二叉树:1 2 3 4 5 6 7 8 9 10 11,后序遍历的结果为:8->9->4->10->11->5->2->6->7->3->1。
(4)层序遍历
它是按广度优先搜索的策略,从根结点出发,依次访问每一层上的节点。这种策略在实际应用中使用较多,如在计算机图形学中用于渲染场景图等。例如对于二叉树:1 2 3 4 5 6 7 8 9 10 11,层次遍历的结果为:1->2->3->4->5->6->7->8->9->10->11
3.1 先序遍历
#include
#include
typedef struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
} TreeNode;
TreeNode* createNode(int val) {
TreeNode *newNode = (TreeNode *)malloc(sizeof(TreeNode));
newNode->val = val;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
void preorderTraversal(TreeNode *root) {
if (root == NULL) {
return;
}
printf("%d ", root->val);
preorderTraversal(root->left);
preorderTraversal(root->right);
}
int main() {
TreeNode *root = createNode(1);
root->left = createNode(2);
root->right = createNode(3);
root->left->left = createNode(4);
root->left->right = createNode(5);
root->right->left = createNode(6);
root->right->right = createNode(7);
root->left->left->left = createNode(8);
root->left->left->right = createNode(9);
root->left->right->left = createNode(10);
root->left->right->right = createNode(11);
printf("前序遍历二叉树结果:");
preorderTraversal(root);
printf("\n");
return 0;
}
运行结果:
![]()
3.2 中序遍历
#include
#include
typedef struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
} TreeNode;
TreeNode* createNode(int val) {
TreeNode *newNode = (TreeNode *)malloc(sizeof(TreeNode));
newNode->val = val;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
void inorderTraversal(TreeNode *root) {
if (root == NULL) {
return;
}
inorderTraversal(root->left);
printf("%d ", root->val);
inorderTraversal(root->right);
}
int main() {
TreeNode *root = createNode(1);
root->left = createNode(2);
root->right = createNode(3);
root->left->left = createNode(4);
root->left->right = createNode(5);
root->right->left = createNode(6);
root->right->right = createNode(7);
root->left->left->left = createNode(8);
root->left->left->right = createNode(9);
root->left->right->left = createNode(10);
root->left->right->right = createNode(11);
printf("中序遍历二叉树结果:");
inorderTraversal(root);
printf("\n");
return 0;
}
运行结果:
![]()
3.3 后序遍历
#include
#include
typedef struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
} TreeNode;
TreeNode* createNode(int val) {
TreeNode *newNode = (TreeNode *)malloc(sizeof(TreeNode));
newNode->val = val;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
void postorderTraversal(TreeNode *root) {
if (root == NULL) {
return;
}
postorderTraversal(root->left);
postorderTraversal(root->right);
printf("%d ", root->val);
}
int main() {
TreeNode *root = createNode(1);
root->left = createNode(2);
root->right = createNode(3);
root->left->left = createNode(4);
root->left->right = createNode(5);
root->right->left = createNode(6);
root->right->right = createNode(7);
root->left->left->left = createNode(8);
root->left->left->right = createNode(9);
root->left->right->left = createNode(10);
root->left->right->right = createNode(11);
printf("后序遍历二叉树结果:");
postorderTraversal(root);
printf("\n");
return 0;
}
运行结果:
![]()
3.4 层次遍历
层次遍历使用queue实现比较好,这里提供C++代码,对于C语言需要自己写一个queue的数据结构。
#include
#include
#include
#include
typedef struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
} TreeNode;
TreeNode* createNode(int val) {
TreeNode *newNode = (TreeNode *)malloc(sizeof(TreeNode));
newNode->val = val;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
void levelOrderTraversal(TreeNode *root) {
if (root == NULL) {
return;
}
std::queue q;
q.push(root);
while (!q.empty()) {
TreeNode *node = q.front();
q.pop();
printf("%d ", node->val);
if (node->left != NULL) {
q.push(node->left);
}
if (node->right != NULL) {
q.push(node->right);
}
}
}
int main() {
TreeNode *root = createNode(1);
root->left = createNode(2);
root->right = createNode(3);
root->left->left = createNode(4);
root->left->right = createNode(5);
root->right->left = createNode(6);
root->right->right = createNode(7);
root->left->left->left = createNode(8);
root->left->left->right = createNode(9);
root->left->right->left = createNode(10);
root->left->right->right = createNode(11);
printf("层次遍历二叉树结果:");
levelOrderTraversal(root);
printf("\n");
return 0;
}
![]()
我的分享也就到此结束啦
如果我的分享也能对你有帮助,那就太好了!
若有不足,还请大家多多指正,我们一起学习交流!
未来的富豪们:点赞→收藏⭐→关注,如果能评论下就太惊喜了!
感谢大家的观看和支持!最后,☺祝愿大家每天有钱赚!!!欢迎关注、关注!