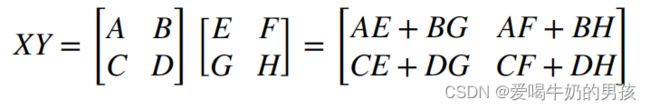【算法设计与分析】分治-第二部分

凸包 Convex Hull

输入：位于同一平面的n个点的集合。

• 假设没有两点具有相同的横坐标
• 假设没有两点具有相同的纵坐标
• 假设没有三点共线

输出：一个表示凸包的集合。可以为点集或者边集

相关题目：

• 洛谷：P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包
• LeetCode：587. 安装栅栏

基本概念

凸包的基本概念

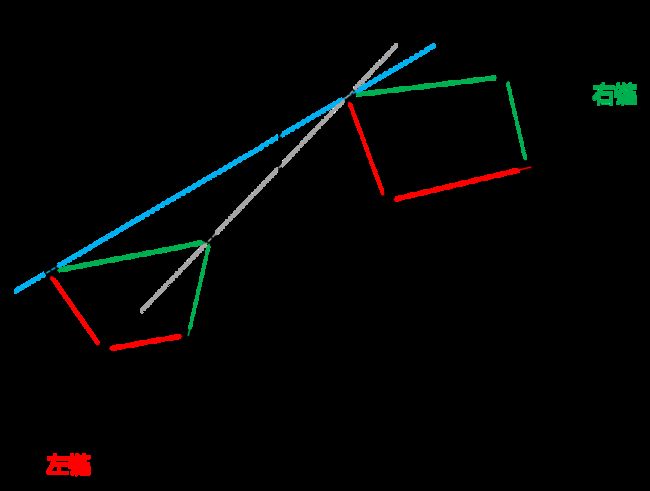
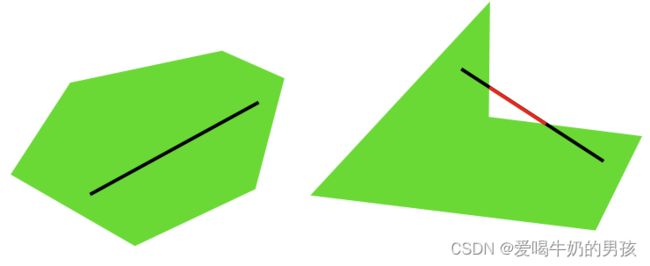
凸多边性：连接凸多边形中的任意两点，均在该凸多边形内部。
图中左边的即为凸多边形，右边的就不是凸多边形。

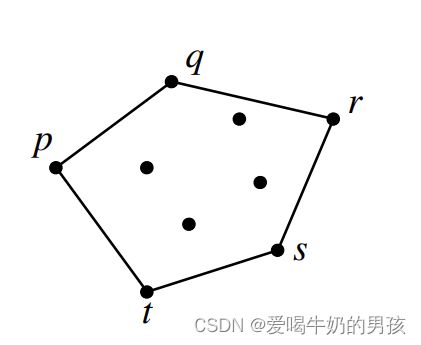
平面上某点集的凸包：包含所有点的最小凸多边形。
如下图所示，这就是一个典型的某个点集的凸包。

凸包的表示方法：一般会使用该凸包的所有的顶点来表示：

• 集合：顶点不按顺序。
• 序列：按照顺时针或者逆时针顺序的某序列。

其他相关知识

向量的叉积：向量$P_1=(x_1,y_1)$ 和 向量$P_2=(x_2,y_2)$，则$P_1\ast P_2=x_1{y}_2-x_2{y}_1$

向量叉积的运用：将向量$P_1$放在$P_2$之前，$P_2$相对$P_1$是向左转还是向右转，由他们的叉积决定：

• 大于0，左转：$P_1\ast P_2=x_1{y}_2-x_2{y}_1>0$
• 等于0，在同一直线上：$P_1\ast P_2=x_1{y}_2-x_2{y}_1=0$
• 小于0，右转：$P_1\ast P_2=x_1{y}_2-x_2{y}_1<0$

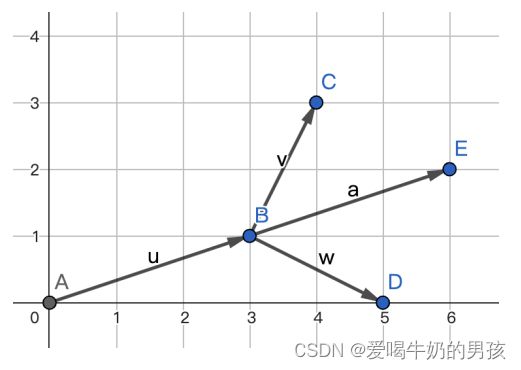
向量叉积在凸包中的运用：给定线段AB和点C，判断AB与C的位置关系。
计算叉积：$(x_B-x_A,y_B-y_A)\ast (x_C-x_B,y_C-y_B)$：

• 大于0：C在AB的左侧
• 等于0：C在AB所在的直线上
• 小于0：C在AB的右侧

就如下图的结果：

• C在AB左侧：$(x_B-x_A,y_B-y_A)\ast (x_C-x_B,y_C-y_B)>0$
• E与AB共直线：$(x_B-x_A,y_B-y_A)\ast (x_E-x_B,y_E-y_B)=0$
• D在AB右侧：$(x_B-x_A,y_B-y_A)\ast (x_D-x_B,y_D-y_B)<0$

穷举法求凸包

输入：n个坐标点，并且不存在三个点共线的情况。
输出：凸包的构成：坐标集合、边集合。

1、对点穷举

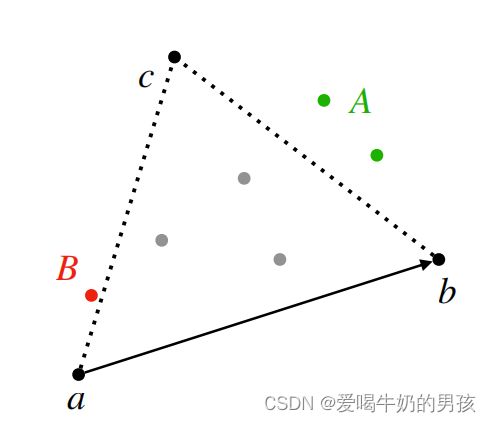
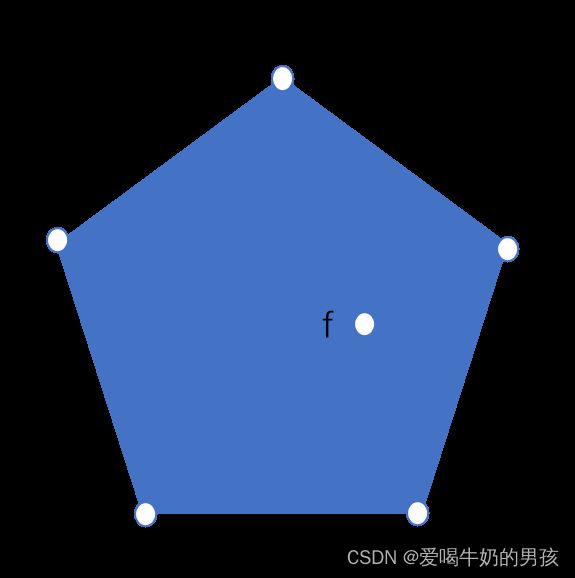
对每一个点，判断其是否在其余任意三个点构成的三角形中。

• 如果 存在 某个三角形包含该点，则说明该点不为凸包的一部分！
  • 下图中 f 点，则存在 三角形abd，包含 f
• 如果 不存在 某个三角形包含该点，则说明该点为凸包的一部分！
  • 对于 a、b、c、d、e 这五个点， 都不存在某一个三角形包含他们。

时间复杂度
穷举每个点的时间复杂度：$O(n)$、穷举除该点之外的其他三个点来构成的三角形的时间复杂度：$O(n^3)$
总的时间复杂度：$O(n^4)$

2、对边穷举

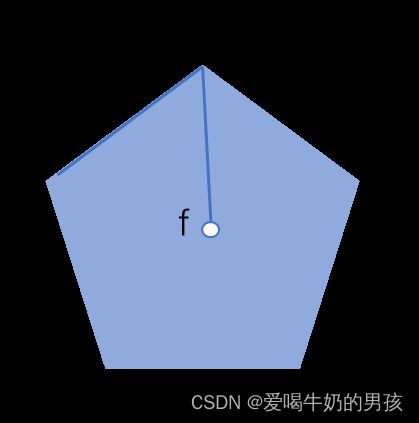
枚举所有的边，再判断剩余的点与边的位置。

• 如果剩余所有点都在边的同一侧，则该边是凸包的组成部分。
  • 下图中，ea 边不存在有两个点，位于边的两侧的情况，因此为凸包的组成部分。
• 如果存在两个点位于边的不同侧，则该边不是凸包的组成部分。
  • 下图中，af 边，存在 e 和 b 这两个点位于边的两侧，因此不为凸包的组成部分。

时间复杂度
穷举每一条边的时间复杂度：$O(n^2)$。 对于边的判断的时间复杂度：$O(n)$
总的时间复杂度：$O(n^3)$

第⼀种分治法 - 插入凸包

分解：将 n 个点分成 A 和 B 两个部分，其中 A 包含 n - 1个点， B 只包含一个点。

• 选取一个特别的点 q 放入 B ：q 是所有点中最右侧的点，该点一定是当前点集中凸包的一部分。
• 不断对 A 进行上述的分解，直至只剩下三个点。

递归过程：对 A不断进行上述的分解，直至递归到基本情况：只剩下三个点。每一次递归，都是求解点集 A 的凸包 CH(A)

递归合并：利用向量的叉积，将 CH(A) 与 B 进行合并，求解整体的凸包。

递归分解

输入如图所示的 10 个点，先将其分解成 A 和 B 两个部分。
此时 A 包含 9 个点，B 包含 1 个点。CH(A) 很明显就是图中的连线部分，但真正求解过程中我们需要不断的将其分解，直至达到基本情况。

中间部分分解过程，如下图所示：

最终，将 A 分解到基本情况：

三个点，一定都属于凸包，即为CH(A)，因此不需要再进行划分。此时不需要向下递归，开始进行递归合并 ：即CH(A) 和 B的合并。

合并凸包

凸包的支撑线：与凸包仅相交于⼀点的直线。
过凸包外一点，仅能得到两条支撑线，如图中的 $q{p}_5$ 和 $q{p}_3$。

右支撑线： 凸包剩余点及内部的点均在支撑线的下方。
左支撑线：凸包剩余点及内部的点均在支撑线的上方。
q与凸包两交点 $p_3$、$p_5$ 将凸包分成两部分
近链：靠近 $q$ 的部分
远链：远离 $q$ 的部分

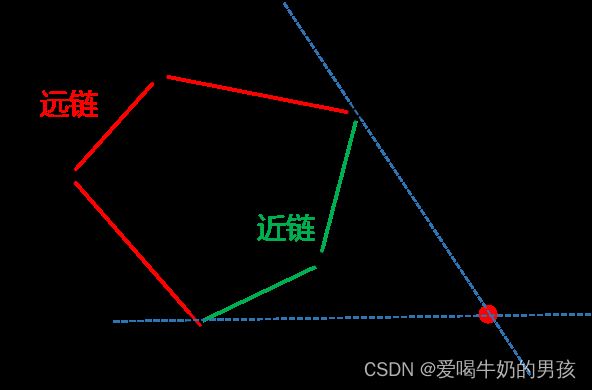
通过观察，可得到，新的凸包，是由 远链 和 左右支撑线 来决定的。
因此合并的主要过程也就是寻找 左右支撑线 。

如果直接枚举求左右支撑线，总共需要 $O(n^2)$的时间复杂度。

可以观察到：凸包上所有的点都在左支撑线的右侧（除左支撑线上的 $p_5$）。
进一步归纳，发现只需要判断凸包与左支撑线交点的相邻两个点（$p_1$、$p_4$）是否在该左支撑线的右侧即可。

寻找左支撑线：从距离q最近的$p_i$ 开始，判断 $p_{(i+1)\%n}$ 和 $p_{(i-1)\%n}$ 是否在左支撑线的右侧。
寻找右支撑线：从距离q最近的$p_i$ 开始，判断 $p_{(i+1)\%n}$ 和 $p_{(i-1)\%n}$ 是否在左支撑线的左侧。

将q 与 远链中包含的点 构成递归的返回值，即递归过程中新的凸包。

时间复杂度

总的时间复杂度 ： $$\begin{gathered} T(n)=T(n-1)+T_{merge} \\ T(n)=O(n)T_{merge} \end{gathered}$$
而 $T_{merge}$ 的主要时间花销就在寻找左右支撑线上，因此 $T_{merge}=O(n)$

所以总的时间复杂度：$T(n)=O(n^2)$

第⼆种分治法 - 归并凸包

分解 ：将 n 个点按照横坐标排序，然后将其分成 A、B两部分，每个部分均包含 n/2 个点。
递归过程：递归求解 A 和 B 的凸包 P和Q。

• 基本情况：不能只考虑 3 个点的情况，还需要考虑会出现 2 个点的情况。

递归合并：对凸包P和Q进行合并。

递归过程

输入 11 个点，第一轮递归过程如下图所示：

对 A 再次递归就会出现基本情况：
此时将 A 均分成两个部分，这两个部分分别有2和3个点，这两种情况均为基本情况，直接返回这些点集即可。

合并凸包

对于递归得到的两个凸包：P 和 Q。

上桥：两个凸包上的两点的连线，且两个凸包剩余的点及凸包内部的所有点均位于上桥的下方。如 $a_1{b}_1$
下桥：两个凸包上的两点的连线，且两个凸包剩余的点及凸包内部的所有点均位于上桥的上方。如 $a_3{b}_3$
右链：某一凸包与上桥的交点按顺时钟到该凸包与下桥的交点中间的点与线。
左链：某一凸包与上桥的交点按逆时钟到该凸包与下桥的交点中间的点与线。

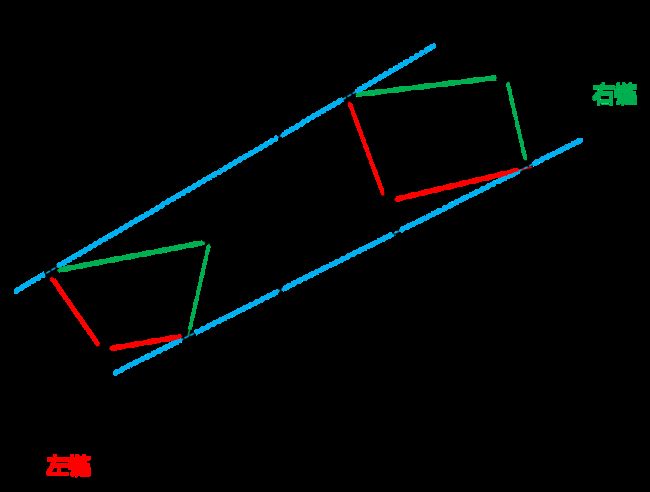
因此合并 P 和 Q 产生的新的凸包 = P的左链 + 上桥 + Q的右链 + 下桥
合并凸包的主要过程就是寻找上桥和下桥。

观察得：
上桥$a_1{b}_1$是$b_1$的右支撑线，是$a_1$的左支撑线。
下桥$a_3{b}_3$是$b_3$的左支撑线，是$a_3$的右支撑线。

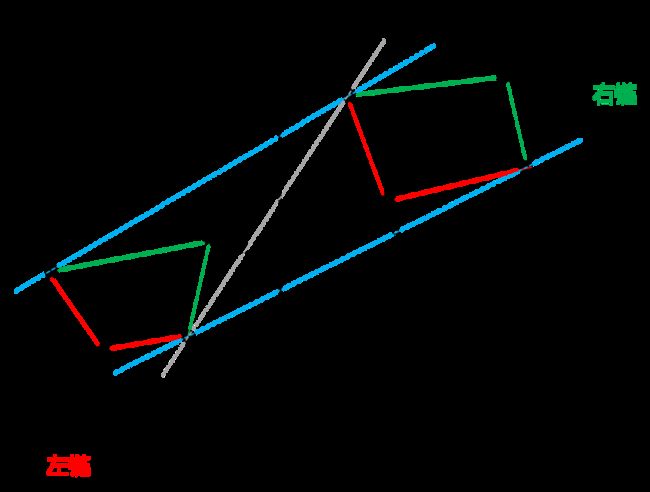
寻找上桥：
令$a_i$是 P 中距离 Q 最近的点，$b_j$是 Q 中距离 P 最近的点。

• 如果$a_i{b}_j$不是$a_i$的左支撑线，则顺时钟检查$b_j$的下一个点。
• 如果$a_i{b}_j$不是$b_j$的右支撑线，则逆时钟检查$a_i$的下一个点。

重复上述的两个步骤，直至找到上桥。
寻找下桥的方式类似，不过方向相反！

初始点为$a_2$ 和 $b_1$

• $a_2{b}_1$是$a_2$的左支撑线。
• $a_2{b}_1$不是$b_1$的右支撑线，逆时钟检查$a_1$。
• $a_1{b}_1$是$b_1$的右支撑线。
• $a_1{b}_1$是$a_1$的左支撑线。
• 满足条件，$a_1{b}_1$即为P和Q的上桥。

时间复杂度

寻找上下桥的时间复杂度，最坏情况就是遍历一遍两边节点之和：$O(n)$，因此$T_{merge}=O(n)$
总时间复杂度：$$\begin{gathered} T(n)=2T(n/2)+T_{merge} \\ T(n)=O(nlogn) \end{gathered}$$

第三种分治法 - 快速凸包

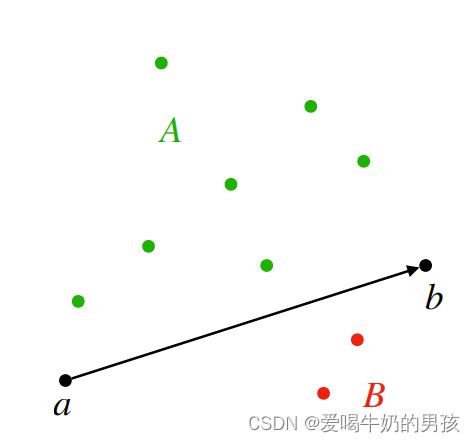
分解：选择最左和最右两点的连线 $ab$ 将其分成两个部分 A 和 B，这两点一定属于凸包。再在A和B中选择距离 $ab$ 最远的点，构成两个三角形，该两点也一定属于凸包。三角形将对应的区域再次划分，三角形内部的点一定不属于凸包，对三角形外部的点进行递归。

递归流程

首先对输入的点集进行预排序，按照x坐标进行排序。
选择最左的点 a ，最右的点 b（这两点一定属于凸包）。

此时$ab$将整个点集分成上下两个部分，A和B。

• 在 A 中选择离 $ab$ 最远的 c（一定属于凸包），连接 $bc$ 和 $ca$，此时a、b、c三点将A分成三个部分。三角形内部的点一定不属于凸包，只需要递归判断 $bc$ 右侧的点，$ca$ 右侧的点。
• B中的操作类似。

一直重复上述递归直至结束。

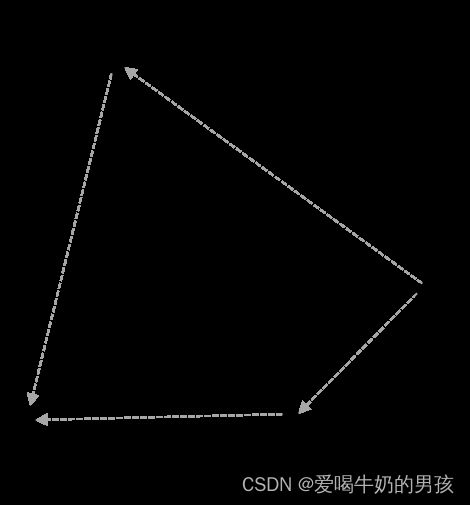
可以将整个递归流程划分成两个步骤：

1. 预排序，寻找最左以及最右的点，将整个点集划分成两个部分，并分别开启递归。 $quick\_hull()$
2. 不断寻找距离划分线右侧点中，距离最远的点。再次将点集其划分成多个部分，再次递归。$quick\_half\_hull()$

quick_hull(S):
    (a,b) <-- sorted_points(S)
    A <-- right_of(S, ba)
    B <-- right_of(S, ab)
    Qa <-- quick_half_hull(A, ba)
    Qb <-- quick_half_hull(B, ab)
    return {a} ∪ Qa ∪ {b} ∪ Qb

quick_half_hull(S, ba):
    if(S == Ø) return Ø
    c <-- furthest(S, ba)
    A <-- right_of(S, bc)
    B <-- right_of(S, ca)
    Qa <-- quick_half_hull(A, bc)
    Qb <-- quick_half_hull(B, ca)
    return Qa ∪ {c} ∪ Qb

时间复杂度

假设 |S| = n、|A|=a、|B|=b。
$quick\_half\_hull()$ 的 运行时间：$T(n)=T(a)+T(b)+O(n)$

• 最好情况 $a=b=n/2$：此时$T(n)=O(nlogn)$
• 最坏情况 $a=0$ $b=n-1$：此时$T(n)=O(n^2)$

$quick\_hull()$ 的运行时间：预排序 + 计算A和B + $quick\_half\_hull()$的递归时间

• 预排序：$O(nlogn)$
• 计算A和B：$O(n)$
• $quick\_half\_hull()$的递归时间：小于 $2T(n)$

因此总时间复杂度：

• 最好情况：$T(n)=O(nlogn)$
• 最坏情况：$T(n)=O(n^2)$

多项式乘法 Polynomial Multiplication

输入：两个n-1次多项式。输入的是从0~n-1次项的系数。
输出：一个2n-2次多项式。输出的是0~2n-2次项的系数。

相关题目：

• 洛谷：P3803 【模板】多项式乘法（FFT）

对于多项式的加法，只需要将相同次数的系数相加即可，时间复杂度：$O(n)$

直接计算

n个系数，分别和另一多项式的n个系数相乘，再对应相加。每一个系数都需要 $O(n)$ 次乘法，$O(n)$次加法。
总体时间复杂度：$O(n^2)$

递归计算

递归关系构建

按照 $x$ 的次数的高低，将 $A$ 和 $B$ 分成两个部分：
$A={\sum }_{i=1}^{n-1}{a}_i{x}^i=A_1+A_2{x}^{n/2}$，其中$A_1={\sum }_{i=0}^{n/2-1}{a}_i{x}^i$，$A_2={\sum }_{i=0}^{n/2-1}{a}_{i+n/2}{x}^i$
$B={\sum }_{i=1}^{n-1}{b}_i{x}^i=B_1+B_2{x}^{n/2}$，其中$B_1={\sum }_{i=0}^{n/2-1}{b}_i{x}^i$，$B_2={\sum }_{i=0}^{n/2-1}{b}_{i+n/2}{x}^i$

此时 $AB=(A_1+A_2{x}^{n/2})\ast (B_1+B_2{x}^{n/2})=A_1{B}_1+(A_1{B}_2+A_2{B}_1)x^{n/2}+A_2{B}_2{x}^n$

$AB$ 是两个 n-1 次多项式的相乘
$A_i{B}_j$ 则是两个 n/2 -1 次多项式相乘

时间复杂度

因此总的时间复杂度：$T(n)=4T(n/2)+O(n)$
令 $T(n/2^k)=O(1)$ 即 $k=lo{g}_{2}n$
所以$$\begin{gathered} T(n)=4^{lo{g}_{2}n}+kO(n) \\ T(n)=O(n^2) \end{gathered}$$

与直接计算的时间复杂度相同，因此不够优。

递归优化

$AB=(A_1+A_2{x}^{n/2})\ast (B_1+B_2{x}^{n/2})=A_1{B}_1+(A_1{B}_2+A_2{B}_1)x^{n/2}+A_2{B}_2{x}^n$

令$A_1{B}_1=P$、$A_1{B}_2=R$、$A_2{B}_1=Q$、$A_2{B}_2=S$
即$AB=P+(R+Q)x^{n/2}+S{x}^n$

再令 $U=(A_1+A_2)(B_1+B_2)=P+R+Q+S$
所以 $R+Q=U-P-S$
因此 $AB=P+(U-P-S)x^{n/2}+S$

相比于计算 $A_1{B}_1$、$A_1{B}_2$ 、$A_2{B}_1$、$A_2{B}_2$这四个不同的值，计算$P$、$U-P-S$、$S$ 只需要得到$P$、$U$、$S$这三个不同的值。
此时 4 次递归，减少到了 3 次递归。

时间复杂度
因此总的时间复杂度：$T(n)=3T(n/2)+O(n)$
令 $T(n/2^k)=O(1)$ 即 $k=lo{g}_{2}n$
所以$$\begin{gathered} T(n)=3^{lo{g}_{2}n}+kO(n) \\ T(n)=O(n^{lo{g}_{2}3})=O(n^{1.585}) \end{gathered}$$

矩阵乘法 Matrix Multiplication

输入：两个 n*n 的矩阵 X与Y
输出：输出两个矩阵的乘积 Z=XY

相关题目：

• 洛谷：B2105 矩阵乘法

直接计算

根据矩阵乘法的定义：$z_{ij}={\sum }_{k=1}^n{x}_{ik}{y}_{kj}$
枚举i、j、k，计算对应的$z_{ij}$。
因此总的时间复杂度：$$T(n)=O(n^3)$$

递归计算

递归关系建立

将矩阵分块，将一个 n*n 的矩阵划分成 4 个 n/2 * n/2 的矩阵。

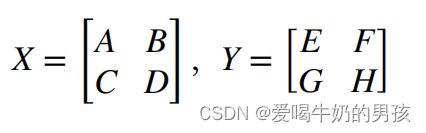
原矩阵的乘法可以基于分块矩阵的乘法来完成。

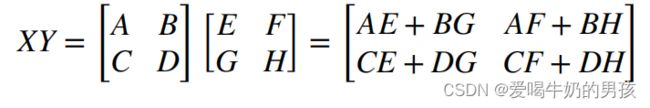
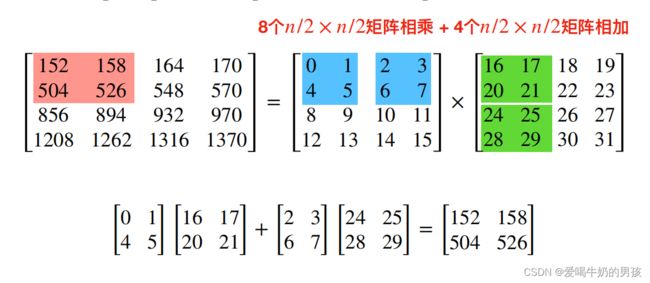
例如：两个 4*4 的矩阵相乘，将这两个 4*4 的矩阵划分成四个 2*2 的分块矩阵，再分别相乘。
计算结果如下图所示：

时间复杂度
n*n的计算过程如图：

n*n 的矩阵划分成 4 个 n/2*n/2 的矩阵，矩阵相乘则有 8 个 n/2*n/2的矩阵相乘 + 4个 n/2*n/2 的矩阵相加。

时间复杂度：$$\begin{gathered} T(n)=8T(n/2)+O(n^2) \\ T(n)=O(n^3) \end{gathered}$$

改进递归关系 - Strassen的技巧

将8个 n/2*n/2的矩阵相乘 + 4个 n/2*n/2 的矩阵相加，优化成7个 n/2*n/2的矩阵相乘 + 11个n/2*n/2 的矩阵相加 + 7个n/2*n/2 的矩阵相减。

定义十个中间矩阵：

• $S_1=F-H$
• $S_2=A+B$
• $S_3=C+D$
• $S_4=G-E$
• $S_5=A+D$
• $S_6=E+H$
• $S_7=B-D$
• $S_8=G+H$
• $S_9=A-C$
• $S_{10}=E+F$

再定义七次矩阵乘法：

• $P_1=A{S}_1=A(F-H)$
• $P_2=S_{2}H=(A+B)H$
• $P_3=S_{3}E=(C+D)E$
• $P_4=D{S}_4=D(G-E)$
• $P_5=S_5{S}_6=(A+D)(E+H)$
• $P_6=S_7{S}_8=(B-D)(G+H)$
• $P_7=S_9{S}_{10}=(A-C)(E+F)$

最终：
$$Z=\begin{array}{cc}{Z}_{11}& Z_{12}\\ Z_{21}& Z_{22}\end{array}=XY$$
因此:

• $Z_{11}=P_5+P_4-P_2+P_6$
• $Z_{12}=P_1+P_2$
• $Z_{21}=P_3+P_4$
• $Z_{22}=P_5+P_1-P_3-P_7$

总共7个 n/2*n/2的矩阵相乘 + 11个n/2*n/2 的矩阵相加 + 7个n/2*n/2 的矩阵相减。

时间复杂度
$$\begin{gathered} T(n)=7\ast T(n/2)+O(n^2) \\ T(n)=O(n^{lo{g}_{2}7})=O{n}^{2.81}) \end{gathered}$$