第6章 密码学和对称密钥算法

6.1 密码学基本知识

6.1.1 密码学的目标

安全从业者可借助密码系统实现4个基本目标：保密性、完整性、身份认证和不可否认性。

其中每个目标的实现都需要满足诸多设计要求，而且并非所有密码系统都是为达到所有4个目标而设计的。

下面的小节将详细讲解这4个目标并简要描述实现目标所必须满足的技术条件。

1. 保密性(confidentiality)

保密性确保数据在静态、传输中和使用中等三种不同状态下始终保持私密。

保密性是指为存储的信息或个人和群体之间的通信保守秘密，它或许是被提得最多的一个密码系统目标。

有两大类密码系统专用于实现保密性。

•对称密码系统(symmetric cryptosystem)，使用一个共享秘密密钥，提供给密码系统的所有用户。

•非对称密码系统(asymmetric cryptosystem)，使用为系统每个用户单独组合的公钥和私钥。

如果你开发的密码系统将用于提供保密性，你必须考虑第5章讨论过的3种不同类型的数据。

•静态数据(data at rest)，或被存储的数据，是指驻留在一个永久位置上等待被访问的数据。

保存在硬盘、备份磁带、云存储服务、USB装置和其他存储介质中的数据都属于静态数据。

•动态数据(data in motion)，或线路上的数据，是指正在两个系统之间通过网络传送的数据。

动态数据可能通过公司网络、无线网络或互联网传送。

•使用中的数据{data in use)，是指保存在计算机系统活跃内存中，可供系统中运行的进程访问的数据。

以上每种情况将带来不同类型的保密性风险，可通过密码抵御这些风险。

例如，动态数据易受窃听的影响，而静态数据则更容易受物理设各盗窃的影响。

如果操作系统没有适当隔离不同进程使用中的数据有可能被未经授权的进程访问。

2. 完整性(integrity)

完整性确保数据没有在未经授权的情况下被更改。

如果完整性机制正常运行，消息的接收者可确定，他收到的消息与发出的消息相同。

同样，完整性检查可确保被存储数据自创建起到被访问时不曾有过更改。

完整性控制抵御所有形式的更改，其中包括第三方试图插入假信息时进行的有意篡改、有意删除部分数据和因传输过程中的故障而发生的无意更改。

消息完整性可通过使用加密的消息摘要来实现；

这个摘要被称为数字签名(digital signature)，是在消息传输时创建的。

消息接收者只需要验证消息的数字签名是否有效，就能确保消息在传输过程中未被改动。

完整性保障由公钥和秘密密钥密码系统提供。

3. 身份认证(authentication)

身份认证用于验证系统用户自称的身份，是密码系统的一项主要功能。

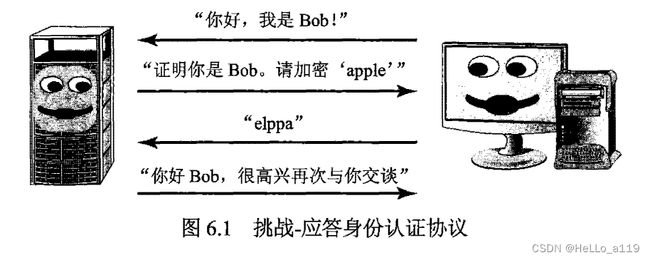
举例来说，假设Bob要与Alice建立一个通信会话，而他俩都是某共享秘密通信系统的参与者。

Alice或许会用一种挑战－应答身份认证技术来确保Bob就是他声称的那个人。

图6.1 展示了这个挑战应答协议在实践中是如何工作的。

在这个例子里，Alice和Bob使用的共享秘密代码相当简单——只是把一个单词的字母颠倒了而已。

Bob首先联系Alice并表明自己的身份。

Alice随后向Bob发这条挑战消息，请Bob用只有Alice和Bob知道的秘密代码加密一条短消息。

Bob回复加密后的消息。Alice证实被加密消息后，确信连接的另一端确实是Bob本人。

4. 不可否认性(non-repudiation)

不可否认性向接收者保证：消息发自发送者，而且没有人冒充发送者。

不可否认性还防止发送者声称自己绝对没有发送过消息（也叫否认消息）。

秘密密钥或对称密钥密码系统（例如简单的替代密码）不提供不可否认性保障。

如果Jim和Bob是同一个秘密密钥通信系统的参与者，那么他们都能用自己的共享秘密密钥生成相同的加密消息。

不可否认性由公钥或非对称密钥密码系统提供，这一主题将在第7章详细讨论。

6.1.2 密码学的概念

与学习任何学科一样，在开始学习密码学之前，你首先必须熟悉某些术语。

下面先来看几个用来描述代码和密码的关键术语。

一条消息在进入编码形式之前被称作明文(plaintext)消息，描述加密功能时用字母P表示。

一条消息的发送者用一种密码算法给明文消息加密(encrypt)，生成一条密文(cipher text)消息，用字母C表示。

这条消息以某种物理或电子方式传送给接收者。

接收者随后用一种预定算法来解密(decrypt)密文消息并恢复明文版本（有关这一流程的演示，请见后面的图6.4) 。

所有密码算法都靠密钥(key)维持安全。

多数情况下，密钥无非是一个数。它通常是一个极大的二进制数，但尽管如此，它也仅是一个数而已。

每种算法都有一个特定密钥空间(key space)。

密钥空间是一个特定的数值范围，而某一特定算法的密钥在这个范闱内才有效。

密钥空间由位大小(bit size)决定。位的大小其实也就是密钥内二进制位(0和1)的数量。

密钥空间指的是从全0密钥到全1密钥的范围。

换句话说，密钥空间是从0到2^n的数范围，其中n是密钥的位大小。

因此，一个128位密钥的值的范围是0到2^128一大致是3.40282367X10^38，这是一个无比庞大的数！

密钥空间对于保护秘密密钥的安全至关重要。

事实上，你从密码得到的安全保护完全取决于你为所用密钥保守秘密的能力。

你会在本章和下一章的学习过程中发现，不同类型的算法会要求使用不同类型的密钥。

在私钥（也叫秘密密钥）密码系统下，所有参与者都使用一个共享密钥。

在公钥密码系统中，每个参与者各有一个密钥对。

密码密钥有时是指密码变量(crypto variable)，美国政府的应用尤其如此。

创建和执行秘密代码和密码的技艺叫密码术(cryptography)。

而与这套实践规范并行的另一项技艺叫密码分析(cryptanalysis), 它研究的是如何打败代码和密码。

密码术和密码分析合在一起，就是我们通常所说的密码学(cryptology)。

一种代码或密码在硬件和软件中的具体实现叫密码系统(cryptosystem)。

联邦信息处理标准(FIPS)140-2“密码模块安全要求“定义了可供联邦政府使用的密码模块的硬件和软件要求。

6.1.3 密码数学

密码学与大多数计算机科学学科一样，能从数学科学中找到它的根基。

要想全面了解密码学，你首先必须了解二进制数学的基本原理以及用来操控二进制值的逻辑运算。

下面将简要描述你应该掌握的一些最基本的概念。

1. 布尔数学(Boolean mathematics)

布尔数学为用于构成任何计算机神经系统的位和字节定义了规则。

你可能非常熟悉十进制系统。这是一个逢十进位的系统，其中的每个位上都有一个整数（从0到9) ，每个位值都是10的倍数。

我们对十进制系统的依赖极可能起源于生物学方面的原因——人类用十根手指头来数数。

同样，计算机对布尔系统的依赖起源于电学方面的原因。

一个电路只会有两种可能的状态——“开”和“关“，前者代表有电流存在，后者代表不存在电流。

电气设备的所有计算都必须用这两个词来表达，因而导致了布尔计算在现代电子学中的使用。

一般来说，计算机科学家把“开”状态称作真(true)值，把“关”状态称作假(false)值。

2. 逻辑运算

密码学涉及的布尔数学利用各种逻辑函数来操控数据。

下面简单介绍其中的几种运算。

AND（与）

''AND”运算（用符号“^”表示）检查两个值是否都真。

表6.1 显示了AND函数的全部4个可能输出的真值表。

在这个真值表中，头两列“X" 和“Y" 展示的是给AND函数的输入值。

请记住，AND函数只取两个变量作为输入。

在布尔数学中，这些变量的每一个都只有两个可能的值(0=FALSE和1=TRUE) ，因此AND函数会有4个可能的输入。

而“X^Y”列则显示了前面两个相邻列所示输入值的AND函数输出。

这种有限数量的可能性使计算机能极其容易地在硬件中执行逻辑函数。

请注意表6.1, 其中只有一种输入组合（即两个输入全为真）产生一个真值输出。

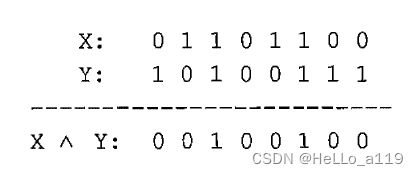
逻辑运算往往在整个布尔词（而非单个值）上进行。请看下面这个例子：

请注意，AND函数是通过比较每列中X和Y的值算出的。只有当列中的X和Y都为真时，输出值才为真。

OR（或）

“OR”运算（用符号“⋁”表示）检查输入值中是否至少有一个为真。

如表6.2所示，该真值表展示了OR函数的所有可能值。

请注意，只有当两个值都为假时，OR函数才返回一个假值。

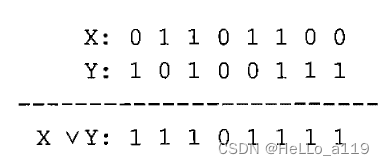
下面还用前面小节的那个例子来展示，如果把X和Y输入OR函数（而不是AND函数）中，会得到什么输出：

NOT（非）

"NOT”运算（用符号”∼”表示）只是颠倒一个输入变量的值。

这个函数一次只在一个变量上运算。表6.3是NOT函数的真值表。

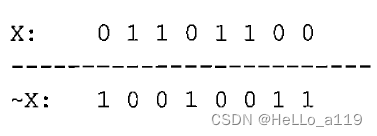
在这个例子中，你可以从前面的例子里取X 值，然后对它运行NOT 函数：

Exclusive OR（异或）

本章介绍的最后一个逻辑函数在密码学应用中或许是最重要和最常用的——“Exclusive OR"（异或）函数。

数学文献把它写成XOR函数，通常用符号”⊕” 表示。

只有当一个输入值为真的时候，XOR函数才返回一个真值。

如果两个值都为假或两个值都为真，则XOR函数的输出为假。

表6.4是XOR运算的真值表。

以下运算显示了将X 和Y 用作XOR 函数的输入时的情况：

3. 模函数(modulo)

模函数在密码学领域极其重要。

不妨回顾一下你小时候初学除法时的情景。

那会儿你还没学过小数，每次做除法题时都要把除不尽的余数写出来。

计算机其实也不懂除法，而这些余数会在计算机运算许多数学函数的过程中发挥关键作用。

模函数非常简单，它是一次除法运算之后留下的余数。

模函数在等式中通常用其缩写“mod" 表示，不过有时也用运算符"%”表示。

下面列举几个模函数的输入和输出：

8 mod 6 = 2

6 mod 8 = 6

10 mod 3 = 1

10 mod 2 = 0

32 mod 8 = 0

32 mod 26 = 6

第7章将探讨RSA公钥加密算法（以发明者Rivest、Shamir 和Adleman 的姓氏命名），届时将再次论及这个函数。

4. 单向函数(one-way function)

单向函数是能方便地为输入的每种可能组合生成输出值的—种数学运算，但这一运算会导致无法恢复输入值。

公钥密码系统全都建立在某种单向函数的基础之上。

但是实践从来没有证明，任何具体的已知函数确实是单向的。

密码学家依赖一些函数，他们相信这些函数是单向的，但是它们被未来的密码分析者破解的可能性始终存在。

下面举一个例子。假设你有一个由三个数相乘得出的函数。

如果你把输入值限制为个位数，则可轻易地逆向还原这个函数并通过查看数字输出来确定可能的输入值。

例如，用输入值1、3、5创建输出值15。但是，假设你把输入值限制为5位素数。

虽然用一台计算机或性能好些的计算器依然可以相当容易地得到输出值，但是逆向还原就没有刚才那么简单了。

对于输出值10 718 488 075 259，你能算出组成它的三个素数吗？没那么容易了，对不对？

原来，这个数是三个素数(17 093、22441和27 943) 的乘积。

由于5位素数总共才有8 363个，所以用一台计算机或一种暴力破解算法或许就能将这道题成功破解，但若想靠心算算出来，这绝

非易事。

5. nonce

密码常通过给加密过程添加随机性来获得强度。实现这一点的方法之一就是使用nonce。

nonce是一个随机数，可在数学函数中充当占位符变量。

每当函数执行时，nonce都会被一个在开始处理时生成的一次性随机数替换。

nonce每次被使用时都必须是一个唯一的数。

比较有名的nonce例子之一是初始化向量(IV)，这是一个随机位串，长度与块大小相同，针对消息执行XOR操作。

当同一条消息每次用同个密钥加密时，IV 用于创建唯一的密文。

零知识证明(zero-knowledge proof)

你向某个第三方证明，你确实知道一个事实，但不把这个事实本身披露给该第三方——这样的机制借助密码学形成，通常通过口令和其他秘密鉴别符实现。

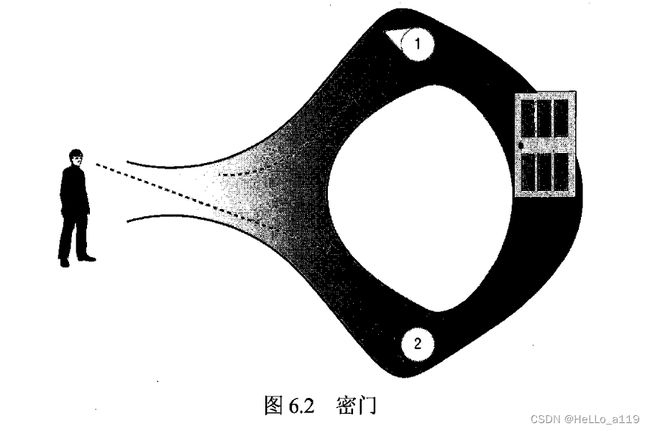
下面用Peggy和Victor这两个人物来说明零知识证明(zero-knowledge proof) 的经典例子。

如图6.2 所示，Peggy知道一个环形岩洞里一道密门的口令。

Victor想从Peggy手里买这个口令，但是他在付钱之前要求Peggy证明自已确实知道这个口令。

而Peggy不愿提前把口令告诉Victor, 担心他知道口令后赖账。零知识证明可以帮助他们走出这个困境。

Victor站在入口处看着Peggy沿通道1出发。Peggy到达密门后用口令打开密门，然后穿过密门沿通道2返回。

Victor目睹Peggy沿通道1出发又从通道2返回的全过程，这证明Peggy必定知道打开密门的正确口令。

在密码学中，零知识证明出现在这样的情况下：

一个人想要证明自已知道一个事实（如口令或密钥），但又不想把这个事实向另外一个人公开。

这可以通过复杂的数学运算实现，如离散对数和图论。

分割知识(split knowledge)

当执行某项操作所要求的信息或权限被分散到多名用户手中时，任何一个人都不会具有足够的权限来破坏环境的安全。

这种把职责分离和双人控制融于一个解决方案的做法叫分割知识(split knowledge)。

密钥托管(key escrow)概念是体现分割知识的最佳例子。

采用密钥托管后，密码密钥会被交给一个第三方妥善保存。

当满足某些条件时，第三方可以用托管密钥来恢复授权用户的访问权限或自行解密资料。

这个第三方叫恢复代理(recovery agent)。

在只使用一个恢复代理的密钥托管安排中，存在着欺诈和滥用这一权限的机会，因为单个恢复代理有可能单方面决定解密信息。

N之取M控制(M of N Control)要求代理总数（N）中至少有M个代理同时在场时才能执行高安全级任务。

因此，执行八之取三控制时，在被指派执行密钥托管恢复任务的八个代理中，只有当三个代理同时在场时才能从密钥托管数据库中

提取一个密钥（其中M总是小于或等于N) 。

代价函数(work function)

你可以用代价函数(work function)或代价因子从耗费成本和/或时间的角度测算破解一个密码系统时需要付出的努力，从而衡量密码系统的强度。

对一个加密系统实施一次完整暴力破解攻击时需要付出的时间和精力，通常是代价函数所代表的内容。

密码系统提供的安全和保护与代价函数/因子的值呈正比例关系。代价函数的大小应与受保护资产的价值匹配。

代价函数略大于该资产的时间值即可。换言之，包括密码保护在内的所有安全措施都应该是有成本效益和成本效率的。

为保护一个资产所付出的努力不应超出它的需求，同时要保证所提供的保护是充分的。

因此，如果信息随时间的推移而逐渐贬值，那么代价函数只要足够为它提供安全保障即可，直到数据完全丧失价值。

挑选密码系统的安全专业人员除了了解数据具有价值的时间长度外，还必须知道新涌现的技术可能对破解密码的努力产生什么影响。

例如，可能会有研究者在第二年发现一种密码算法的一个缺陷，使该算法保护的信息变得不再安全。

同样，基于云的平行计算和量子计算技术在经过一段时间的发展之后，可能会令暴力破解攻击的可行性大增。

6.1.4 密码

密码系统已被力求保护通信保密性的个人和政府使用了很长时间。

下面各节将介绍密码的定义，同时探索构成现代密码基础的几种常用密码类型。

务必记住，这些概念看起来属于基本概念，但若把它们组合在一起，将给密码分析者带来可怕的对手，使他们长时间陷于挫败之中。

1. 代码与密码

人们往往交替使用代码(code)和密码(cipher)这两个词，但从技术角度看，不能将这两个词混为一谈。

二者在概念上有重要区别。代码是由代表单词和矩语的符号构成的密码系统；

尽管代码有时是保密的，但它们并不一定提供保密性保护。执法机关采用的“10号通信系统”是代码的一个常见例子。

在这套系统下，＂我收到你的通信且已知晓其中内容”这句话用代码短语“10-4" 表示。

旗语和莫尔斯电码也是代码的例子。这些代码人尽皆知，也确实给通信带来了方便。

有些代码是保密的。它们通过一个秘密代码簿传递机密信息，而对于代码簿上的代码，只有发送者和接收者知道它们的含义。

例如，一个间谍用“老鹰已着陆”这句话来报告敌军派来一架飞机这一消息。

而密码则始终要隐藏消息的真实含义。密码通过各种技术手段更改和重新排列消息的字符或位，以实现保密性。

密码以位（即一个个位二进制代码）、字符（即ASCH消息的单个字符）或块（即消息的一个固定片段，通常以位数表示）为单位将消息从明文转变成密文。

以下各节将介绍当今使用的几种常见密码。

2. 移位密码(transposition cipher)

移位密码(transposition cipher)通过一种加密算法重新排列明文消息的字母，形成密文消息。

解密算法只需要逆向执行加密位移便可恢复原始消息。

本章中图6.1列举的那个挑战-应答协议例子用一个简单的移位密码颠倒了消息的字母顺序，使“apple" 变成“elppa”。

移位密码的实际应用比这复杂得多。例如，你可以用一个关键词进行列移位(columnar transposition)。

下面这个例子尝试用秘密密钥“attacker“ 给消息“The fighters will strike the enemy bases at noon" 加密。

首先提取关键词字母，然后按字母表顺序给它们标注数字。

第一个出现的字母A接受的值为1, 字母表上第二靠前的字母被赋值2。

按字母表顺序出现的下一个字母C被标注为3, 以此类推。下面是由这个顺序得出的结果：

接下来，在关键词的字母下面按顺序把消息的字母逐个写出。

最后，发送者以每列逐字母往下读的方式给消息加密；各列读出的顺序与第一步分配的数字对应，产生的密文如下：

在另一端，接收者用密文和相同的密钥重建8列矩阵，逐行读出明文消息。

3. 替换密码(substitution cipher)

替换密码(substitution cipher)通过加密算法用一个不同的字符替换明文消息的每个字符或位。

被古罗马时代征战欧洲的朱利叶斯·凯撒用来与身在罗马的西塞罗传递消息的密码，便是最早成名的替换密码之一。

凯撒对送信途中存在的各种风险心知肚明——没准哪个送信人就是敌人的奸细，而且说不定哪个送信人会在路上遭遇敌人的埋伏。

出于这方面的考虑，凯撒开发了一个密码系统，被后人称作凯撒密码(Caesar cipher)。

这个系统非常简单。加密一条消息时，将字母表上的每个字母向右移3位即可。例如，A变成D, B变成E。

如果你在这个过程中到达字母表的末尾，则返回来从头开始使用字母表即可，即X变成A,Y变成B,Z变成C。

出于这一原因，凯撒密码还被称作ROT3（或Rotate 3, 轮转3)密码。

凯撒密码是一种采用单一字母替换法的替换密码。

这里举一个实际使用凯撒密码的例子。

下面第一行是原始语句，第二行则是用凯撒密码加密后看上去像句子的东西。

你只需要将每个字母向左移3位，便可解密这条消息。

可将每个字母逐个转换成它的十进制等同物（其中A为0, z为25) ，从而以数学方式表述ROT3密码。

这时，可通过给每个明文字母加3来形成密文。

不妨用“密码数学”小节讨论的模函数来说明这个环绕。凯撒密码的最终加密函数如下所示：

C = (P + 3) mod 26

与之对应的解密函数如下：

P = (C - 3) mod 26

与移位密码的情况一样，目前存在许多比本章所举例子更复杂的替换密码。

多表替换密码在同一条消息中使用多个字母表，以此给破解制造障碍。

多表替换密码系统的最著名例子之一是Vigenere 密码系统。

Vigenere密码使用一个加密/解密图，如图6.3所示：

请注意，这张图在报头下重复写出26个字母（共26遍），每遍移动一个字母。

使用Vigenere系统时需要一个密钥。譬如，这个密钥是MILES。接下来，可以执行以下加密流程：

(1) 写出明文。

(2) 在明文下面写出加密密钥，按需要重复这个密钥，直到形成一行与明文长度相同的文本。

(3) 把每个字母位置从明文转变成密文。

①定位以第一个明文字符开头的列(A) 。

②定位以第一个密钥字符开头的行(S) 。

③定位这两项的交叉处，在这里写下所出现的那个字母(S) 。这就是该字母位置的密文。

(4) 在明文中为每个字母重复步骤(1)至步骤(3) 。

多表替换虽然可以抵御直接频率分析，但是当遇到名为周期分析(period analysis)的二阶式须率分析时就显得无能为力了——周期分析根据密钥的重复使用情况进行频率分析。

4. 单次密本(one-time pad)

单次密本(one-time pad)是极其强力的一种替换密码。

单次密本为明文消息中的每个字母使用一个不同的替换字母表。

它们可用以下加密函数表示，其中K是用于将明文字母P加密成密文字母C加密密钥：

C = (P + K) mod 26

单次密本通常被写成很长的一系列数字以插入函数。

单次密本的优势在于，如果使用得当，它将是不可破解的。

字母表替换中不存在任何重复模式，这使密码分析成了无用功。

不过，必须满足几点要求才能保证算法的完整性。

•单次密本必须随机生成。若使用从一本书中摘取的短语或段落，将使密码分析者有机会破解代码。

•单次密本必须处于物理保护之下，以防泄露。敌人如果拿到密本拷贝，将能轻松破解经过加密的消息。

•每个单次密本必须只使用一次。

如果密本被重复使用，密码分析者将能在用同一密本加密的多条消息之间比较相同点，进而有可能确定所使用的密钥值。

事实上，使用纸质密本的一种常见做法是在用完之后把写有密钥材料的纸张销毁，以免密本被再次使用。

•密钥必须至少与将被加密的消息一样长。这是因为，密钥的每个字符只用于给消息中的一个字符编码。

这些要求中若有任何一项未被满足，单次密本原本让人无法破解的特质就会立刻失灵。

事实上，密码分析员破解了一个依赖单次密本的欧洲某国绝密密码系统，造就了美国情报机构的一次重大成功。

这个代号为VENONA的计划发现，该国在为其密本生成密钥值时惯用一种模式。

这个模式的存在违背了单次密本密码系统的第一项要求：密钥必须随机生成，不可使用任何重复模式。

整个VENONA计划已于最近解密，所有内容在美国国家安全局网站上对公众开放。

单次密本有着悠久的历史，被用来保护极其敏感的通信。

单次密本始终未被推广使用，这主要是因为人们实在难以生成、分发和保护所要求的冗长密钥。

由于密钥长度的问题，单次密本在现实中只能用于较短的消息。

5. 运动密钥密码(running key cipher)，书密码(book cipher)

密码密钥长度有限，自然存在许多密码漏洞。

如前所述，单次密本使用的密钥至少与消息一样长，从而规避了这些漏洞。

然而，单次密本执行起来却非常棘手，因为它们需要物理交换密本。

化解这个困境的一种常见方法是使用运动密钥密码(running key cipher)，这种密码也叫书密码(book cipher)。

在这种密码中，加密密钥与消息本身一样长，而且往往选自一部普通图书、一张报纸或一本杂志。

例如，发送者和接收者提前达成一致，把《白鲸》的一章文本（从第3段开始）用作密钥。

他们两人只需要按必要的数量用连续的字符来执行加密和解密操作。

举一个例子。假设你要用前面刚讲的密钥加密消息“Richard will deliver the secret package to Matthew at the bus station tomorrow“ 。

这条消息长66个字符，因此你要使用运动密钥的头66个字符“With much interest I sat watching him. Savage though he was, and hideously marred”。

接下来，通过这个密钥，你可以用任何算法给明文消息加密。

再举一个模26加法的例子一模26加法将每个字母分别转换成一个十进制的对等体，把明文加到密钥上，然后进行模26运算，以得出密文。

如果你给字母A赋值0, 给字母Z 赋值25, 你可对明文的头两个词进行以下加密运算。

接收者收到密文后使用同样的密钥，然后从密文中减去密钥，进行模26运算，最终将得出的明文转回字母字符。

6. 块密码(block cipher)

块密码(block cipher)在消息“块“上运算，在同一时间对整个消息执行加密算法。

移位密码是块密码的例子。挑战－应答算法使用的简单算法提取整个词，然后反向排列词的字母。

比较复杂的列移位密码在整条消息（或消息的某个片段）上运算，用移位算法给消息和一个秘密密钥加密。

大多数现代加密算法都执行某类块密码。

7. 流密码(stream cipher)

流密码(stream cipher)一次在消息（或消息流）的一个字符或一个位上运行。

凯撒密码是流密码的一个例子。单次密本也是一种流密码，因为算法在明文消息的每个字母上单独运行。

流密码也可发挥某种类型块密码的作用。这种运算会用实时数据填满一个缓冲区，然后把数据加密成块并传送给接收者。

8. 混淆(confusion)和扩散(diffusion)

密码算法依靠两种基本运算混淆(confusion)和扩散(diffusion)来隐藏明文消息。

使用混淆运算时，明文和密钥之间有着极复杂的关系，以至于攻击者不能只靠改动明文和分析结果密文来确定密钥。

使用扩散运算时，明文中发生的一点变化会导致多个变化在整个密文中传播。

请设想这样一个例子：一种密码算法首先进行一次复杂的替换，然后通过移位重新排列被替换密文的字符位置。

在这个例子中，替换带来的就是混淆，移位带来的就是扩散。

6.2 现代密码学

现代密码系统通过复杂算法（在计算上很复杂的算法）和长密码密钥来实现密码学的保密性、完整性、身份认证和不可否认性目标。

以下各节将首先讨论密码密钥在数据安全领域中扮演的角色，然后介绍当今常用的三类算法：对称加密算法、非对称加密算法和哈希算法。

6.2.1 密码密钥

早期密码学有一条“通过隐匿获得安全”的主导原则。

当时的一些密码学家认为，确保一种加密算法安全的最佳方法是把算法的细节藏匿起来，不让外人知道。

老密码系统要求通信双方保守秘密，不让第三方知道用于加密和解密消息的算法。

算法的任何泄露，都有可能导致整个系统被敌人破解。

现代密码系统不依靠算法的保密性。

事实上，大多数密码系统的算法都会在相关文献和互联网上广泛公开，供公众查看。

面向大众公开算法，其实可以敦促算法不断提高自身安全性。

计算机安全界对算法的广泛分析，使从业者得以发现和纠正算法的潜在安全漏洞，确保其使用的算法可以最妥善地保护通信安全。

现代密码系统不再依靠秘密算法，而是依靠一个或多个密码密钥的保密性，而这些密钥将用于为特定用户或用户群体个性化定制算法。

回顾一下前面讨论的移位密码；这种密码用一个关键词通过列移位来引导加密和解密。

用于执行列移位的算法人尽皆知——你从本书就读到了它的细节！

然而，列移位还可用于保护两方之间的通信只要选用的关键词不会被外人猜出即可。

只要这个关键词是安全的，就不必在意第三方知不知道算法细节。

如本章前面所述，单次密本算法之所以强度高，主要是因为它使用了一个极长的密钥。

事实上，这种算法的密钥至少与消息本身一样长。

大多数现代密码系统都不会使用这么长的密钥，但是在决定密码系统的强度以及确定加密是否有可能被密码分析技术破解时，密钥的

长度依然是极其重要的因素。

较长的密钥通过提升密钥空间的大小来提供级别更高的安全，从而加大暴力破解攻击得逞的难度。

计算能力的快速提高允许你在加密工作中使用越来越长的密钥。

然而，试图击败你的算法的密码分析者也会掌握同样强大的计算能力。

因此，你若想超越敌手，就必须使用在长度上足以挫败当前密码分析能力的密钥。

此外，若想使自己的数据更有可能抵御密码分析的纠缠并安全无恙地维持到未来的某个时候，你还必须在数据应当保持安全的整个时期内设法使用超过密码分析能力预期发展步伐的密钥。

例如，正如本章前面讨论过的那样，量子计算的出现，可能会给密码学带来翻天覆地的变化，使当前使用的密码系统变得不再安全。

当“数据加密标准”(DES)在1975年出台的时候，56位密钥被认为足以确保任何数据的安全。

然而，如今业界已取得广泛共识：由于密码分析技术的进步和超级计算能力的涌现，56位DES算法已不再安全。

现代密码系统用至少128位的密钥来保护数据，使其不被人偷窥。

请记住，密钥的长度与密码系统的代价函数直接相关：密钥越长，密码系统就越难被破解。

除了选择长密钥，并在预期的信息保密时间内保持密钥安全之外，你还应该落实一些其他的密钥管理实践规范。

•始终安全地存储密钥，如果你必须通过网络传输密钥，则应采取适当的方式，使密钥免遭未经授权的泄露。

•尽可能以随机性高的方法选择密钥，充分利用整个密钥空间。

•当密钥不再被需要时，安全地将它们销毁。

6.2.2 对称密钥算法

对称密钥算法依靠一个分发给所有通信参与者的“共享秘密“加密密钥。

这个密钥被各方用来加密和解密消息，因此，发送者和接收者拥有一个共享的密钥拷贝。

发送者用这个共享秘密密钥加密，而接收者用它来解密。

当使用的密钥极大时，对称加密会变得非常难以破解。

这样的密钥主要用于进行海量加密，只提供保密性安全服务。

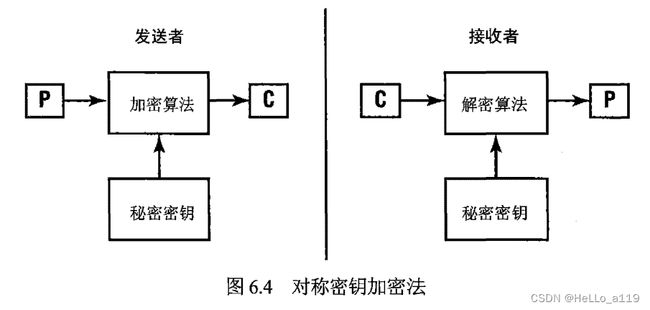
对称密钥加密法也叫秘密密钥密码(secret key cryptography)和私钥密码(private key cryptography)。

图6.4 显示了对称密钥加密和解密的过程（图中的“C" 代表密文消息，“P”代表明文消息）。

有时候，对称密钥会与只用于一次会话的短暂密钥一起使用。

这种情况下使用的密钥被称为临时密钥(ephemeral key)。

最常见的例子是传输层安全(TLS)协议，它用非对称密码建立一条加密信道，然后切换到使用临时密钥的对称密码。

你将在第7章学到更多有关这个主题的知识。

————————————————————————————————————————

注意：

（private key)这个词有些不太好解释，因为它是三个不同术语的成分，具有两个不同的含义。

私钥这个词本身永远都是指公钥密码（亦称非对称密码）密钥对中的私钥。

然而，无论是私钥密码还是共享私钥，都属于对称密码。

“私”这个字的含义被延伸为：涉及两个人，他们共享一个共同保守的秘密。

而“私”这个字的真实含义其实只涉及一个人，由他来保守一个秘密。

切勿在学习中弄混了这几个词。

————————————————————————————————————————

对称密钥加密法有几个弱点。

•密钥分发是主要问题。

双方在通过一个对称密钥协议建立通信之前，首先必须找到一种安全的方法来交换秘密密钥。

如果这时没有现成的安全电子信道可供使用，则往往需要采用一种安全的线下密钥分发方法（即带外交换）。

•对称密钥加密法不提供不可否认性。

由于任何通信方都能用共享的秘密密钥对消息进行加密和解密，因此无法证明一条消息到底是从何处发出的。

•算法缺乏可扩展性。

如果通信群体规模较大，将很难使用对称密钥加密法。

只有在每个可能的用户组合都共享一个私钥的情况下，才能在群体内的个人之间实现安全的私密通信。

•密钥必须经常重新生成。

每当有参与者离开通信群体时，该参与者知道的所有密钥都必须弃用。

在自动加密系统中，密钥可以根据经过的时间长度、交换的数据量或者会话空闲或终止的事实重新生成。

对称密钥加密法的主要优势在于它的运算速度。

对称密钥加密非常快，往往比非对称算法快1 000到10000倍。

从数学的属性看，对称密钥加密法本身自然更适合硬件执行，从而为更高速的运算创造机会。

稍后的“对称密码”一节将详细讨论主要秘密密钥算法在当今的使用情况。

6.2.3 非对称密钥算法(asymmetric key algorithm)

非对称密钥算法(asymmetric key algorithm)可提供解决方案以消挕对称密钥加密的弱点。

公钥算法(public key algorithm)是非对称算法中最常用的例子。

在这些系统中，每个用户都有两个密钥：一个是所有用户共享的公钥，另一个是只有用户自已知道并保守秘密的私钥。

但这里也有复杂的地方：相反和相关的两个密钥必须一先一后用于加密和解密。

换言之，如果公钥加密了一条消息，则只有对应的私钥可解密这条消息，反之亦然。

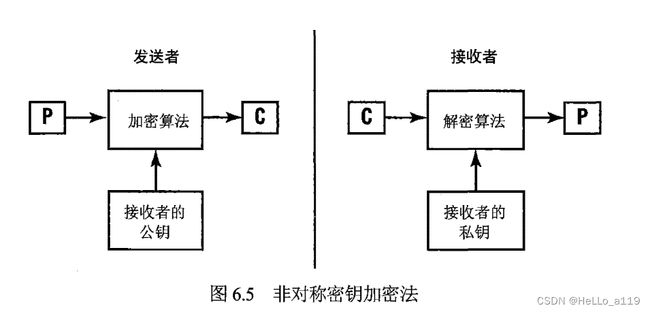
图6.5展示了公钥密码系统中用于加密和解密消息的算法（其中“C”代表密文消息，“P"代表明文消息）。

举个例子。如果Alice想用公钥密码给Bob发一条消息，她应该首先创建这条消息，然后用Bob的公钥给消息加密。

解密这个密文的唯一可能手段是Bob的私钥，而且唯一有权访问这个密钥的只有Bob本人。

因此，Alice给消息加密后，连她本人也无法将其解密。

如果Bob想回复Alice, 他只需要用Alice的公钥给消息加密，而Alice用自己的私钥解密消息后便可以浏览了。

秘钥要求：

最近，在本书的一位作者的课堂上，一名学生希望了解与对称加密算法相关的可扩展性问题。

对称加密系统要求每对潜在通信者都必须拥有一个共享受私钥，这种情况使算法丧失了可扩展性。

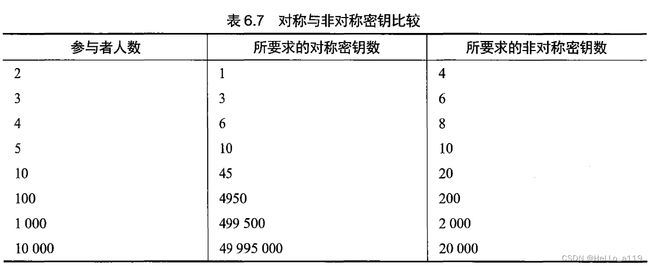
通过对称密码完全连接n个参与方所要求的密钥总数可从下式得出：

密钥数＝n(n-1)

这么来看，事情好像没那么糟（而且这不是针对小系统的），但考虑到表6.7展示的这组数字，你可能就不这么想了。

显然，人数越多，对称密码系统能满足需要的可能性就越低。

非对称密钥算法还支持数字签名技术。

我们基本上还用前面那个例子：如果Bob要向其他用户保证，有他署名的一条消息确实是他发送的，那么他首先要用一种哈希算法（下一节会介绍各种哈希算法）创建一个消息摘要。Bob随后用自己的私钥给这个摘要加密。任何想验证签名的用户只需要用Bob的公钥解密消息摘要并验证被解密消息摘要的准确性。第7章将详细说明这个过程。

下面讲述非对称密钥加密法的主要长处。

•添加新用户时只需要生成一个公钥－私钥对。

这个密钥对可被用来与非对称密码系统的所有用户通信。算法因此而具有极高的可扩展性。

•便于从非对称系统移除用户。

非对称密码系统提供了一个密钥注销机制，该机制可用于取消一个密钥，进而从系统有效移除一个用户。

•只需要在用户私钥失信的情况下重新生成密钥。

一个用户离开社区时，系统管理员只要宣布该用户的密钥失效。只要其他密钥没有失信，就没必要为任何其他用户重新生成密钥。

•非对称密钥加密可提供完整性、身份认证和不可否认性。

只要一个用户没有把自己的私钥泄露给别人，由该用户签名的消息就可显示为准确无误、来自特定来源，而且事后不可否认。

非对称密码可用于创建提供不可否认性的数字签名，这一点将在第7章讨论。

•密钥分发简便易行。

想加入系统的用户只需要把自己的公钥提供给任何通信对象。任何人都不可能从公钥推导出私钥。

•不需要预先建立通信关联。

两个人从开始通信的那一刻起始终保持通信安全。非对称加密法不要求以预先建立关系的方式提供数据交换安全机制。

公钥密码的主要弱点是运算速度缓慢。

由于这一原因，许多需要安全传输大量数据的应用先用公钥密码建立连接，以此交换一个对称秘密密钥，然后安排剩余的会话使用对称加密法。这种综合使用对称与非对称密码的方法叫混合密码(hybrid cryptography)。

表6.8 比较了对称和非对称的密码系统。

仔细研究这张表，你会发现，一个系统的一个弱点恰恰可以被另一系统的长处弥补。

6.2.4 哈希算法

前一节的学习让你了解到，公钥密码系统与消息摘要配套使用时可提供数字签名能力。

消息摘要（也叫哈希值或指纹）是由哈希算法生成的消息内容归纳（与文件校验和没什么不同）。

从理想哈希函数推导消息本身的做法即便可能实现，其过程也极其困难，而且两条消息几乎不可能产生相同的哈希值。

一个哈希函数为两种不同方法产生相同值的情况被称为碰撞(collision)，而碰撞的存在通常会导致哈希算法贬值。

第7章将详细介绍当前的哈希算法，说明可以怎样用它们来提供数字签名能力，而数字签名将有助于实现密码的完整性和不可否认性目标。

6.3 对称密码

你已学习了对称密钥加密法、非对称密钥加密法和哈希函数的基本概念。

以下各节将深入探讨几种常用的对称密码系统。

6.3.1 密码运行模式

密码的运行模式是指密码算法为实现抵御攻击的充分复杂度而采用的转换数据的不同方式。

密码的主要运行模式有:

•电子密码本(ECB)模式

•密码块链接(CBC)模式

•密码反馈(CFB)模式

•输出反馈(OFB)模式

•计数器(CTR)模式

•Galois/计数器模式(GCM)

•带密码块链接消息验证码的计数器(CCM)模式

1．电子密码本模式(Electronic Code Book, ECB)

电子密码本(Electronic Code Book, ECB)模式是最容易理解的简单模式，也是最不安全的模式。

算法每次处理一个64位块，它只用选好的秘密密钥给块加密。

这意味着，算法如果多次遇到同一个块，将会生成相同的加密块。

如果敌人在窃听通信，那么他们很容易根据所有可能的加密值构建一个“密码本＂。

收集到足够数量的块后，便可用密码分析手段来解密其中的一些块并破解加密方案。

这一漏洞使ECB模式变得无法使用——但最短的传输除外。

在日常工作中，ECB模式只用来交换少量数据，例如用于启动其他密码模式的密钥和参数以及数据库的计算单元。

2. 密码块链接模式(Cipher Block Chaining, CBC)

在密码块链接(Cipher Block Chaining, CBC)模式中，每块未加密文本在被加密之前，都要先借助前面刚生成的密文块接受异或(XOR)运算。

解密流程只需要解密密文并进行反向异或运算。

CBC执行一个初始化向量(IV)并用第一个消息块进行异或运算，每次运算生成一个唯一的输出。

必须将IV发送给接收者，可能以明文形式将IV附在完成的密文前面，也可能用加密消息的同一个密钥对IV实施ECB模式的加密保护。

使用CBC模式时，错误传播是需要考虑的一个重要问题——如果一个块在传输过程中被毁坏，那么这个块以及后面的块将无法解密。

3. 密码反馈模式(Cipher Feedback, CFB)

密码反馈(Cipher Feedback, CFB)模式是CBC 模式的流密码版。

换句话说， CFB针对实时生成的数据进行运算。但是，CFB模式不把消息分解成块，而是使用与块大小相同的存储缓冲区。

系统在缓冲区填满时给数据加密，然后把密文发送给接收者。

接下来，系统等待缓冲区再次被新生成的数据填满，然后将它们加密并传输。

CFB 并非使用原先就有的数据，而是使用实时数据，除了这一点外，CFB采用的方式与CBC相同。

它使用了一个IV, 并且使用了链接。

4. 输出反馈模式(Output Feedback, OFB)

在输出反馈(Output Feedback, OFB)模式下，密码以与CFB模式几乎完全相同的方式运行。

所不同的是，OFB不是对前一个密文块的加密版进行异或运算，而是用一个种子值对明文进行异或运算。

对于第一个被加密的块，OFB用一个初始化向量来创建种子值。

而后面的种子值则通过算法在前一个种子值的基础上运算得出。

OFB模式的主要优势在于，不存在链接函数，传输错误不会传播，因而不会影响后面块的解密。

5. 计数器模式(Counter, CTR)

计数器(Counter, CTR)模式使用了与CFB和OFB模式类似的流密码。

但是，CTR模式并非根据以前的种子值结果为每次加密/解密运算创建种子值，而是利用一个简单的计数器为每次运算增量。

与OFB模式一样，CTR模式不会传播错误。

6. Galois/计数器模式(Galois/Counter Mode, GCM)

Galois/计数器模式(Galois/Counter Mode, GCM)采用标准CTR加密模式，并添加了数据真实性控制，可确保接收方所接收数据的完整性。这一点是通过向加密过程添加身份认证标记(authentication tag)来实现的。

7. 带密码块链接消息验证码的计数器模式

与GCM类似，带密码块链接消息验证码的计数器模式(CCM)把保密性模式与数据真实性流程结合到了一起。

在这种情况下，CCM密码把用于保证保密性的计数器(CTR)模式与用于保证数据真实性的密码块链接消息验证码(CBC-MAC)算法融为一体。

CCM只用于具有128位块长度并要求每次传输必须使用不同nonce的块密码。

———————————————————————————————————————————————————

注意：

GCM和CCM模式都同时包含了保密性和数据真实性。

它们因而被称作经过验证的加密模式。而ECB、CBC、CFB、OFB和CTR模式只提供保密性，因而被称作未经验证的模式。

———————————————————————————————————————————————————

6.3.2 数据加密标准

美国政府于1977年发布“数据加密标准”，并提议将其用作所有政府通信的标准密码系统。

由于算法存在缺陷，密码学家和联邦政府现已不再认为DES是安全的。

业界广泛认为，情报机构可随意解密用DES加密的信息。

DES后于2001年12月被“高级加密标准”取代。

但是即便如此，还是应当了解DES, 因为它是下一节即将讨论的一种更强（但依然还不够强）的加密算法”三重DES" (3DES) 的基础构件。

DES是一种64位块密码，共有5种运行模式：

•电子密码本(ECB)模式

•密码块链接(CBC)模式

•密码反馈(CFB)模式

•输出反馈(OFB)模式

•计数器(CTR)模式

DES的所有模式都是一次性在64位明文上进行运算，以生成64位密文块。

DES使用的密钥长56位。

DES通过长长的一系列异或(XOR)运算生成密文。

这个过程会为每个加密/解密操作重复16遍。

每一次重复通常被称为一轮加密——这解释了DES需要执行16轮加密的说法。

每轮加密都生成一个新密钥，该密钥将被用作随后加密轮次的输入。

————————————————————————————

注意：如前所述，DES用56位密钥推动加密和解密进程。

不过，你可能从一些文献上读过，DES使用64位密钥。

这两种说法其实并不矛盾，我们完全可以从逻辑上解释清楚。

DES规范要求使用64位密钥。但是在这64位中，只有56位含密钥信息。

余下的8位应该包含奇偶校验信息，以确保其他56位准确无误。

但是实践中很少使用这些奇偶校验位。你将56这个数字记住即可。

————————————————————————————

6.3.3 三重DES

前面讲过，“数据加密标准”(DES) 的56位密钥不再被认为足以应对现代密码分析技术和超级计算能力。

但是，改进版的DES, 即“三重DES''(3DES) ，却能通过相同的算法产生更强的加密，不过，这已不再被认为能够满足现代要求。

出于这一原因，应该避免使用3DES加密——尽管现在依然有许多产品支持3DES。

3DES有多个不同变体，每个变体都使用了不同数量的独立密钥。

头两个变体DES-EDE3和DES-EEE3使用了3个不同的独立密钥：K1、K2和K3。

这两个变体的区别在于它们执行的运算，分别用字母E代表加密，D代表解密。

DES-EDE3用K1给数据加密，用K2解密得出的密文，然后用K3加密文本。

DES-EDE3可用以下表达式表示，其中E(K,P)代表用密钥K给明文P加密，D(K，P）代表用密钥K给密文C解密： E(K1,D(K2,E(K3，P)））。

另一方面，DES-EEE3用所有的3个密钥依次给数据加密，可表示为：E(K1,E(K2,E(K3，P)））。

———————————————————————————————————

提示：

如果你想知道EDE模式中为什么包含一次解密运算，那么我们告诉你，这是创建算法和为DES提供向后兼容性的过程产生的一个不可思议的结果。

加密和解密是可逆的运算，因此，即便采用了解密功能，我们依然可以把它视为一轮加密。

———————————————————————————————————

从数学的角度来说，DES-EEE3和DES-EDE3应该具有168位有效密钥长度。

然而，针对这一算法的已知攻击把算法的有效强度降到了112位。

DES-EEE3是当前被NIST认为安全的唯一一个3DES变体。

3DES 的其他变体DES-EDE1，DES-EEE2和DES-EDE2使用1个或2个密钥，重复多次使用同一个密钥，但这些模式已不再被认为安全。

值得一提的是，美国NIST最近宣布弃用3DES的所有变体，并且将在2023年年底禁止把它们用于联邦政府应用。

———————————————————————————————————

注意：

本节的讨论引出一个明显的问题——双重DES(2DES)究竟发生了什么？

你将在第7章发现，双重DES曾被拿来尝试过，但是当它在中间相遇攻击下被证明还不如标准DES安全时，很快就被弃用了。

———————————————————————————————————

6.3.4 国际数据加密算法

“国际数据加密算法”(IDEA)块密码是在业界普遍抱怨DES算法缺乏充分密钥长度的情况下开发出来的。

与DES一样，IDEA在64位明文/密文块上运行。不过， IDEA是用一个128位密钥开始运算的。

这个密钥在一系列运算中被分解成52个16位子密钥。

子密钥随后通过异或与模运算的结合作用到输入文本上，以产生输入消息的加密/解密版。

IDEA能在DES使用的5种模式(ECB、CBC、CFB、OFB和CTR)下运行。

IDEA算法由它的瑞士开发者取得专利。但专利于2012年到期，如今已能无限制地使用。

在Phil Zimmerman颇受欢迎的“良好隐私" (Pretty Good Privacy, PGP)安全邮件软件包中，

可以看到IDEA的一种流行执行方案。第7章将详细讨论PGP。

6.3.5 Blowfish

Bruce Schneier的Blowfish块密码是DES和IDEA的另一个替代方案。

Blowfish与它的前身一样，在64位文本块上运行。不过，Blowfish允许密钥长度变化（其中最短为相对不太安全的32位，最长为极强的448位），从而进一步扩展了IDEA的密钥强度。

显然，密钥的加长会导致加密/解密时间的相应增加。

但时间试验证明，Blowfish这种算法比IDEA和DES的速度要快得多。

况且Schneier对公众开放Blowfish, 使用它时不需要任何许可证。

Blowfish加密算法已被许多商用软件产品和操作系统采用。有大量Blowfish资料可供软件开发人员参考。

6.3.6 Skipjack

Skipjack算法被美国政府在联邦信息处理标准(FIPS)185“ 托管加密标准”(EES) 中批准使用。

与许多块密码一样，Skipjack在64位文本块上运行。它使用80位密钥，支持DES支持的4种运行模式。

Skipjack很快被美国政府接受，提供支持Clipper和Capstone加密芯片的密码例程。

然而，Skipjack多了一点复杂性，因为它支持加密密钥托管。

两家政府机构——美国NIST和财政部，各持有重建Skipjack密钥所需信息的一部分。

执法部门得到合法授权后，可联系这两家机构以获取密钥片段，然后便能解密所涉两方之间的通信。

Skipjack和Clipper芯片并不受密码界欢迎，这在很大程度上是因为美国政府的现行托管规程并不值得信任。

6.3.7 Rivest Ciphers

Rivest-Shamir-Adleman (RSA) Data Security公司的Ron Rivest多年来创建了系列对称密码，业界称之为Rivest Ciphers(RC)算法家族。

其中的RC4、RC5和RC6在当今发挥了特别重要的作用。

1. Rivest Cipher 4 (RC4)

RC4是Rivest于1987年开发的一种流密码，在随后的几十年里被广泛使用。

它只进行一轮加密，允许使用40~2048位的长度可变密钥。

RC4之所以被使用得这么普遍，是因为它被集成到有线等效隐私（WEP)、Wi－Fi 保护访问(WPA)、安全套接字层(SSL)和传输层安全(TLS)等协议之中。

这一算法遭遇的一系列攻击使其在今天的使用已变得不安全。

由于这个以及其他原因，WEP、WPA和SSL不再符合现代安全标准，而TLS也不再允许把RC4用作流密码。

2. Rivest Cipher 5 (RCS)

RC5是一种块大小可变(32、64或128位）的块密码，所用密钥大小为0~2040位。

需要指出的是，不能把RC5简单看作RC4的下一个版本。

事实上，它与RC4算法完全无关。

相反，RC5被认为是不再安全的旧算法RC2的改进版。

RC5接受了暴力破解试验。测试者借助大量业界计算资源开展了一次大规模行动，试图破解一条用64位密钥RC5加密的消息，但这次行动花了四年多时间才破解了这条消息。

3. Rivest Cipher 6 (RC6)

RC6是作为RC5的下一个版本而开发的一种块密码。它采用128位块大小，允许使用128、192或256位对称密钥。

这一算法曾是下一节将讨论的“高级加密标准”(AES) 的候选算法之一，但是没有被选中，今天也没有被广泛使用。

6.3.8 高级加密标准    

2000年10月，美国国家标准与技术研究院(NIST)宣布，Rijndael（读作“rhine-doll")块密码被选中用来代替DES。

2001年11月，NIST发布FIPS 197, 强制规定美国政府必须用AES/Rijndael给所有敏感非涉密数据加密。

“高级加密标准”(AES)密码允许使用3 种密钥强度：128、192和256位。

AES只允许处理128 位块，但Rijndael 超出了这个规定，允许密码学家使用与密钥长度相等的块大小。

加密的轮数取决于所选密钥的长度。

• 128位密钥要求10轮加密。

• 192位密钥要求12轮加密。

• 256位密钥要求14轮加密。

6.3.9 CAST

CAST算法是另一个被集成进一些安全解决方案的对称密钥块密码家族。

CAST算法使用了Feistel网络，有两种表现形式：

• CAST-128用大小为40~128位的密钥对64位明文块进行12~16轮Feistel网络加密。

• CAST-256用大小为128、160、192、224或256位的密钥对128位明文块进行48轮加密。

CAST-256算法曾经是“高级加密标准”的候选算法，但是没有被选中。

Twofish

Bruce Schneier（也是Blowfish的创造者）开发的Twofish算法是AES的另一个终极品。

与Rijndael一样， Twofish是一种块密码。它在128位数据块上运行，能够使用长达256位的密码密钥。

Twofish使用的两项技术在其他算法中是找不到的。

预白化处理(prewhitening)  第1轮加密前用一个单独的子密钥对明文进行异或运算。

白化后处理(postwhitening) 第16轮加密后执行同样的运算。

6.3.10 比较各种对称加密算法

许多对称加密算法是你需要掌握的。

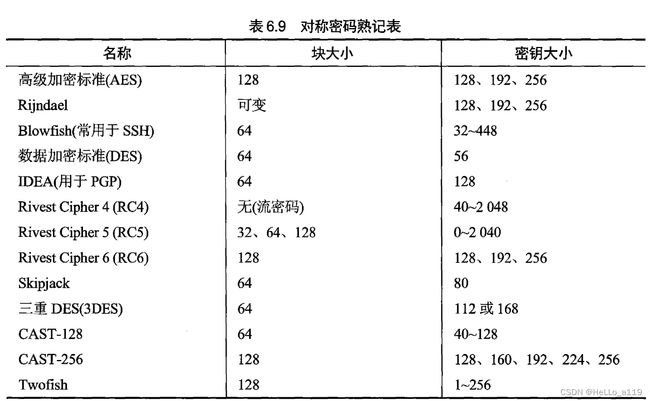
表6.9列出了几种常用和知名的对称加密算法，同时标出了它们的块大小和密钥大小。

表6.9是考试重要内容！

6.3.11 对称密钥管理

由于密码密钥所含信息对于密码系统的安全至关重要，密码系统的用户和管理员有责任采取超常措施保护密钥材料的安全。

这些安全措施统称为密钥管理实践(key management practice)规范，其中包括涉及秘密密钥的创建、分发、存储、销毁、恢复和托管的防护手段。

1. 创建和分发对称密钥

如前所述，涉及对称加密算法的主要问题之一是运行算法所需秘密密钥的安全分发。

安全交换秘密密钥的方法主要有三种：线下分发、公钥加密和Diffie-Hellman密钥交换算法。

•线下分发

这种在技术上最简单（但存在物理上的不便）的方法涉及密钥材料的物理交换。

一方向另一方提供写了秘密密钥的一张纸或装有秘密密钥的一块存储介质。

在许多硬件加密设备中，这一密钥材料以电子设备的形式交付，由这个电子设备将实际密钥组装在一起，插入加密设备中以供使用。

然而，每种线下密钥分发方法都有自己固有的缺陷。

如果密钥材科通过邮递发送，可能会被人拦截。

电话可能被人窃听。写有密钥的纸张可能被人无意中扔进垃圾桶或丢失。

使用线下分发的方法会给最终用户带来麻烦，特别是当他们处于地理位置遥远的地方时。

•公钥加密

许多通信者希望享受秘密密钥加密的速度好处而免去分发密钥的麻烦。

出于这一理由，许多人首先利用公钥加密建立一个初步通信连接。

成功建立这个连接且各方相互验证身份后，他们便可通过这个安全的公钥连接交换秘密密钥。

随后，他们将通信从公钥算法转换到秘密密钥算法，以享受不断提高的处理速度。

一般来说，秘密密钥加密在速度上要比公钥加密快数千倍。

•Diffie-Hellman

有时，无论是公钥加密还是线下分发，都不能满足需求。

双方可能需要直接相互沟通，但他们之间没有可用来交换密钥材料的物理手段，而且没有现成的公钥基础设施以便交换秘密密钥。

这种情况下，Diffie-Hellman之类的密钥交换算法被证明是最实用的机制。

2. 存储和销毁对称密钥

使用对称密钥加密法的另一个重大挑战是，必须确保密码系统使用的所有密钥的安全。

这包括遵循有关加密密钥存储的最佳实践规范：

•绝不将加密密钥与被加密数据保存在同一个系统里，否则会让攻击者轻易入侵！

•对于敏感密钥，考虑安排两个人各持一半片段。这两人以后必须同时到场才能重建整个密钥。这就是所谓分割知识原则（本章前面曾经讨论过）。

当一名知道秘密密钥的用户从本机构离职或不再被允许访问被该密钥保护的材料时，必须更换密钥，而且必须用新密钥重新加密所有加密材料。

挑选密钥存储机制时，可从两个选项中进行选择：

•基于软件的存储机制 可把密钥作为数字对象保存到使用它们的系统里，例如，把密钥存进本地文件系统。

更高级的基于软件的机制可能用专门的应用程序来保护密钥，包括通过二次加密防止有人未经授权访问密钥。

基于软件的方法往往简便易行，但却会引入软件机制遭破坏的风险。

•基于硬件的存储机制 是专用于管理密钥的硬件设备。

它们可能是个人设备，例如个人用来保存密钥的闪存驱动器或智能卡，也可能是企业设备，被称为硬件安全模块(hardware security module, HSM)，用于为机构管理密钥。

硬件方法比软件方法更复杂，执行起来成本也更高，但它们能够提供额外的安全保护。

3. 密钥托管和恢复

密码是一种强有力的工具。与大多数工具一样，它不仅可用于诸多有益目的，还可用来实现恶意企图。

面对密码技术的爆炸性发展，各国政府提出了使用密钥托管系统的主张。

这些系统允许政府在有限的情况下（如按照法院的命令）从一个中央存储设施获取密码密钥并将其用于某一特定通信。

过去10年来，被提出用于密钥托管的方法主要有两种。

•公平密码系统 在这种托管方法中，用于通信的秘密密钥被分解成两个或多个片段，每个片段都被交付给一个独立的第三方保管。

每个密钥片段都不能单独发挥功效，但各个片段被重新组合到一起后可以形成秘密密钥。

政府部门得到可以访问特定密钥的合法授权后，要向每个第三方出示法庭命令的证明，然后才能重新组合秘密密钥。

•托管加密标准 这种托管方法向政府或另一授权代理提供了解密密文的技术手段。

这种方法是专门针对Clipper芯片提出的。

政府监管部门几乎不可能越过为广泛执行密钥托管而设置的必要法律和隐私障碍。

技术可能是现成的，但普通公众可能永远不接受由此带来的潜在政府侵权。

然而，密钥托管在机构内也有合法用途。当相关人员从机构离职，而其他员工需要访问被加密的数据时，或者当密钥丢失时，密钥托管和恢复机制会体现出它们的价值。

在这些方法中，密钥恢复代理(recovery agent, RA)能够恢复分配给各个用户的加密密钥。

当然，这是一种极为强大的特权，因为RA可以访问任何用户的加密密钥。

出于这个原因许多机构选择采用一种名为N之取M控制的机制来恢复密钥在这和方法中，机构中有一组规模为N的人员被授予RA 特权。

如果他们想要恢复加密密钥，则小组中必须至少有M名成员同意这样做。

例如，在N= 12、M=3的N之取M控制系统中，12名得到授权的恢复代理里必须至少有3名同时在场，才可恢复加密密钥。

6.4 密码生命周期

除了单次密本以外，所有密码系统的使用寿命都是有限的。

摩尔定律对计算能力发展趋势的预测已被普遍接受。

它指出，最先进的微处理器的处理能力大约每两年会提高一倍。

这意味着，处理器迟早会达到能随意猜出通信所用加密密钥的力量级别。

安全专业人员在挑选加密算法时，必须重视密码生命周期问题，且必须通过适当的管治控制确保无论需要在多长时间内保证受保护信息不泄密，所选中的算法、协议和密钥长度都足以保持密码系统的完整性。

以下是可供安全专炒人员使用的算法和协议管治控制：

•规定机构可接受的密码算法，如AES、3DES和RSA。

•根据被传输信息的敏感性识别可与每种算法配套使用的可接受密钥长度。

•枚举可用的安全交易协议，如TLS。

举例来说，如果你在设计一个密码系统以保护预计将在下周启动的业务计划的安全，你完全没有必要担心10年后是否会有一台能把这些计划破解出来的处理器被开发出来。

另一方面，如果你要保护的是可能用来建造原子弹的信息，那你几乎肯定会要求这一信息在未来10年里始终保密！