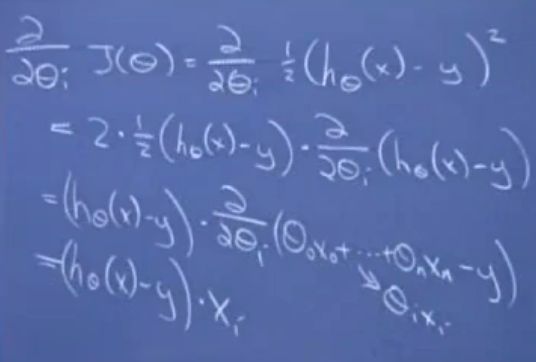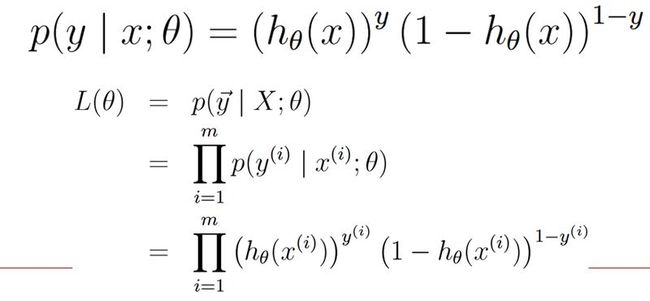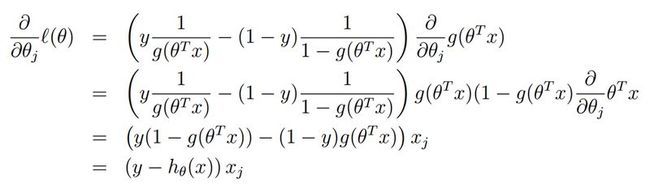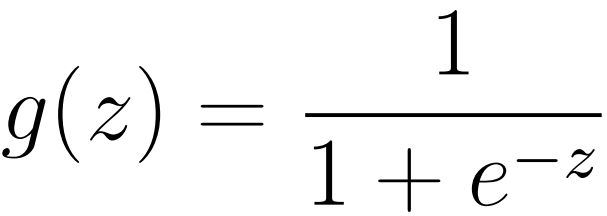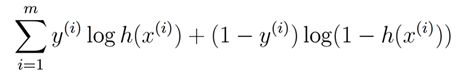Logistic回归
Logistic回归
Part I: 线性回归
线性回归很常见,给你一堆点,作出一条直线,尽可能去拟合这些点。对于多维的数据,设特征为xi,设函数h(θ)=θ+θ1x1+θ2x2+....θnxn为拟合的线性函数,其实就是内积,实际上就是y=wTx+b
那么如何确定这些θ参数(parament)才能保证拟合比较好呢?
1.1 使用最小二乘法的目标函数
我们易有这样的二次目标函数:J=min∑mi=112(h(θ)−yi)2 ,m即所有数据条数。
该目标函数的意义在于:误差最小化。这就是最小二乘法。
h(θ) 中的h即是hypothesis(假设的意思),h函数是我们的算出结果,yi是我们的实际结果,平方的作用有两个,一是是代替ABS,二方便求导。
想要实现目标函数,然后求出θ,最传统的是矩阵方法(最小二乘法拟合最常用的数学方法),θ=(XTX)−1XTY。
该式子来自于二维最小二乘法(一次拟合、忽视偏置=就一个方程):θ∑Ni=1x2i=∑Ni=1xiyi
如果你是使用MATLAB之类的话,那么就是几行代码的事。如果是C/JAVA,还是乖乖使用下面的梯度下降算法(Gradient Descent)。
值得注意的事,矩阵方法要计算矩阵的逆(慢、而且可能不存在、且编程麻烦),复杂度O(n^3),在数据量较大的时候,效率会被梯度下降算法爆掉。
1.2 梯度下降算法
计算机是很笨的。如果想要确定某个值,那么有一种很笨的方法:迭代法。
设定一个边界初值(最大or最小),然后一小步一小步的去变化这个值并验证,知道最后逼近最优值,停止迭代。
由于目标函数是最小化,我们有这个古老的算法。
θnewi=θoldi−α∂∂θJ(θ)
至于原理,参照wiki的解释,这样调整θ,会使得目标函数不停的收敛,同时偏导的梯度控制了收敛的速度。
首先把各个θ设为零,让其从一个平衡状态,在迭代过程中缓慢修改。
减小的量由alpha(学习率,由数据大小确定,既要防止调整过大,也要防止调整过小)*目标函数J的偏导数构成。
经验规则表明,对于Tanh/Logistic激活函数,初始学习率在0.1是个不错的选择,如果训练过程中迅速过拟合,或出现NaN,表明学习率过大。
降一个量级或除以2试试。对于线性激活函数,如果误差波动较大,可以适当的降低量级。
调整各个θ的同时,目标函数J的计算值也在减小,向局部最小值移动。
同时梯度的下降速度由疾变缓,在最后的迭代过程中,梯度将会趋于0,从而能够保证较为精确的逼近目标值。这样,既保证了目标函数的最小化,又求出的参数θ。
1.3 偏导数的处理
假设只有一条数据。目标函数J的偏导数你可以化简一下。链式法则求导。
最后的求导结果是一个非常神奇的式子:(h(θ)−y)∗xi
如果是多条数据呢?累加偏导结果即可。
θnewi=θoldi−∑mj=1α(hθ(xj)−yj)∗xji
由此诞生了三种常用训练梯度算法。
1.4 三种梯度训练梯度方法
一、批梯度算法(BGD,Batch Gradient Descent)
正如上面的式子,先扫每个维度,然后扫全部数据累计θ的变化值
for(i:维度)
for(j:数据条数)
θnewi=θoldi−∑mj=1α∗(h(θ)−yj)∗xji
每次迭代复杂度O(n^3), 下场是:慢。
二、随机梯度算法(SGD,Stochastic Gradient Descent)
它的改良就是,调整循环顺序,每次只取一条数据作为误差,将h(θ)预处理,去求梯度,而不是放在两层循环下变成三层循环去求个总梯度。
for(j:数据条数)
calch(θ)
for(i: 维度)
θnewi=θoldi−α∗(h(θ)−yj)∗xji
每次迭代复杂度O(n^2)
PS. 关于常量b的求法,即对b的偏导*alpha,b=α∗(h(θ)−yj)
这种算法偷工减了一层for,并且带来了更少的迭代次数(实测,批:50次,随:35次)下场就是,最后的近似值没有批梯度精确,不过够用了。
三、迷你批梯度算法(mBGD,Mini-Batch Gradient Descent)
深度学习中使用。每次取一小段数据做完全梯度,而不是只用一个。在速度和精度之间做了一个均衡。
SGD是BatchSize=1的特例,即每次更新只对一个样本误差取梯度。BGD是BatchSize=ExampleSize的特例,每次更新对全部样本取梯度。
为了平衡计算,mini-batch里把跑完全样本梯度一次称为epoch,跑一个batch称为iter。
训练方法具体参考:Theano深度学习分析
1.5 迭代问题
如何确定迭代的次数?我们大可以设个500,让它一直算下去,然而还是有一些停止技巧。
①目标函数收敛判断法(浅层学习)
迭代停止条件目前分为两个。设精度是0.001
一、近似达到目标函数的局部最小值,即变化小于0.001
二、各个参数Θi的变化小于0.001(可选)
一般达到这两个条件,迭代就可以考虑停止了。
②交叉验证&Early-Stopping(深度学习)
在Deep Learning里,单纯看目标函数是不靠谱的,我们只能根据目标函数下降,来判断学习的有效进行。
但是我们并不能知道学习情况。尤其是加入L1/L2惩罚后,目标函数的比例会出现问题。
更严重的是,过拟合情况很难从目标函数中发现。有时候目标函数还在下降,其实已经过拟合很严重了。
这时候就需要Early-Stopping,所以引入交叉验证手段(需要对训练样本划分验证集),具体参考:Theano深度学习分析
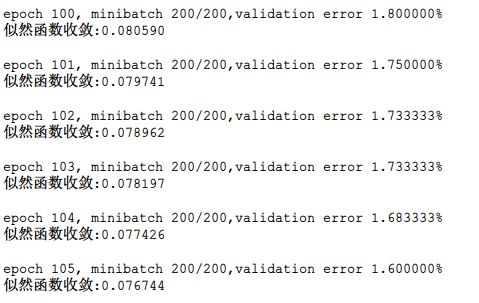
其中,每次epoch,测一次验证集,根据验证集错误率下降情况,判断过拟合,这是训练深度神经网络的基本功。
(下图是训练一个人脸检测的CNN,加了L2惩罚,似然函数比往常大了一个量级,交叉验证直观反应了训练情况)
1.6 优化:局部加权回归
拟合时,我们希望离预测点比较远的点分配比较小的权重,而离的比较近的点分配比较大的权重。
这样,拟合时,拟合的出的线将不是一条单调的直线(容易欠拟合,不能很好适应数据特征),而是一条随数据摆动的曲线。
这样就带来新的问题:过拟合,即随着数据不停摆动(可以理解成把所有数据点用折线连起来),容易受到噪声数据影响,导致拟合效果奇差。
因此,局部加权回归比较吃数据,也比较难调整,用不好基本就完蛋,但是某些大师很喜欢用(来自Andrew NG的吐槽)。
根据距离远近分配权重由高斯核函数(又名径向基核函数)完成。
f=e∣∣xi−x∣∣2−2k2
距离采用的是欧拉距离(同KNN),k值是这个核函数唯一需要调整的地方。
通常取值有0.001,0.01,0.1,1,10,k越小,离预测点越近的点越容易分配到比较大的权重,就越容易过拟合。
加权方法:
for(每一个预测点)
for(每条样本数据)
计算该条数据的加权xnewi=f∗xoldi
然后利用加权过后的xnewi进行拟合
Part Ⅱ Logistic回归
Logistic回归中文又叫逻辑回归。它和线性回归的最大区别在于:它将线性回归结果,通过Logistic函数生成概率,从而进行0/1分类。
尽管Logistic函数是非线性的(S形,平滑),然而它的功能只是生成概率,而不是非线性划分数据。
所以Logistic回归只对线性可分的数据的效果比较好,对于线性不可分数据,需要使用含有将数据映射到高层空间的,BP神经网络网络或SVM神经网络。
2.1 概率论与目标函数设计的原理
已有xji,若求出θ,则yj即可回归算出。这是一个事实。
那么假如用P(yj|xji;θ)表示拟合出yj的概率,当然这个概率不是说高就高,说低就低的,它近似服从正态(高斯)分布。
我们的任务是设计很科学的θ,使得利用样本数据造成的概率分布尽可能接近正态分布,也就是说估计出θ的近似值。
这样的模型称之为判别模型(Discriminate Model),判别模型可以用于分类/回归。
假设P(yj|xji;θ)服从正态分布,那么就有了概率密度函数,利用概率密度函数,反过来设计一个对θ的似然估计函数L(θ)
于是最终任务便变成:基于假设下,利用最大似然估计方法求出θ。
由于最大化L(θ)式子与最小二乘法的式子很接近,于是近似认为最大似然方法等效于最小二乘方法,这便是最小二乘法的概率论角度的解释。
2.2 误差服从二项分布的目标函数
由于Logistic回归用于二类分类时,y的取值非0,即1。上述的正态分布,则变成二项分布。
由二项分布,有如下的概率分布。
P(y=0|x;θ)=h(θ)
P(y=1|x;θ)=1−h(θ)
合并这两个分布为一个式子P(y|x;θ),即概率分布函数,这里由于y取值的特殊性,所以有以下优美的指数式子(方便取对数似然函数)
于是有关于y的概率密度函数,取对参数θ的似然估计,就是估计出最准确的θ,累乘概率密度函数。
老样子,log取对数,化累乘为累加
求偏导数。
然后你就会发现这个偏导结果怎么那么耳熟?怎么和那个回归的最小二乘法J函数的偏导结果差不多。
真是个优美的式子。于是你又可以用梯度下降算法了。
不同的是,这次你得让似然函数取最大值,也就是说,参数θ初始设为0,然后慢慢增加,直到似然函数取得最大值。这其实是梯度上升算法。
2.3 概率映射Logistic函数——化回归为分类,Logistic回归之本质
关于分类与回归,不同在于y的取值类型。连续型叫回归,离散型叫分类。当然一般分类指的是二类分类问题。回归的方法固然可以拿来回归分类问题。
一个简单的方法就是对于最后回归出的连续型y,加上阶跃函数(负0正1),转化为离散型y。这就是60年代盛行的线性神经网络,即Rosenblatt感知器。
Logistic回归在线性回归+阶跃函数的基础做了改良,对线性回归结果使用了Logistic-Sigmoid函数,这样h(Θ)=Sigmoid(内积)。
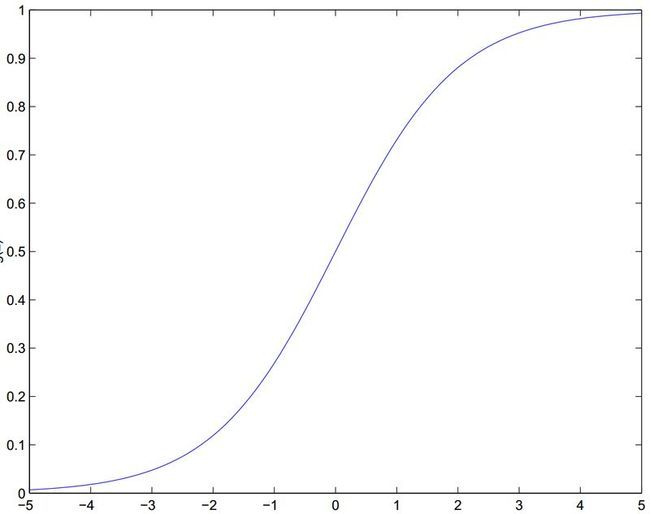
Logistic函数值域[0,1],非线性双端饱和,平滑,目前广泛用于概率生成函数 。可以参考:限制Boltzmann机
有效定义域范围[-3,3],所以要对输入进行进行处理,尽量缩放至[-1,1]。
有一个非常容易混淆的地方,就是神经网络的Sigmoid隐层激活函数和这里概率生成函数作用是不同的。
Sigmoid除了有良好的概率生成能力之外,还有非线性加强输入的能力(中央区域强化信号,两侧区域弱化信号)
在神经网络中会用来做激活函数。可以参考:ReLu激活函数
2.4 迭代问题
迭代终止条件最重要的是保证似然函数的近似值最大且收敛。
也就是说,每次迭代时,都要算一算这个似然目标函数的值,不出意外,应该是逐步增长,速度由快到慢,最后收敛于一个值的。注意这里h(Θ)要经过sigmoid函数处理,不然log会爆的。
2.5 C++代码
#include "cstdio"
#include "iostream"
#include "fstream"
#include "vector"
#include "sstream"
#include "string"
#include "math.h"
using namespace std;
#define N 500
#define delta 0.0001
#define alpha 0.1
#define cin fin
struct Data
{
vector<int> feature;
int y;
Data(vector<int> feature,int y):feature(feature),y(y) {}
};
struct Parament
{
vector<double> w;
double b;
Parament() {}
Parament(vector<double> w,double b):w(w),b(b) {}
};
vector<Data> dataSet;
Parament parament;
void read()
{
ifstream fin("traindata.txt");
int id,fea,cls,cnt=0;
string line;
while(getline(cin,line))
{
stringstream sin(line);
vector<int> feature;
sin>>id;
while(sin>>fea) feature.push_back(fea);
cls=feature.back();feature.pop_back();
dataSet.push_back(Data(feature,cls));
}
parament=Parament(vector<double>(dataSet[0].feature.size(),0.0),0.0);
}
double calcInner(Parament param,Data data)
{
double ret=0.0;
for(int i=0;i<data.feature.size();i++) ret+=(param.w[i]*data.feature[i]);
return ret+param.b;
}
double sigmoid(Parament param,Data data)
{
double inner=calcInner(param,data);
return exp(inner)/(1+exp(inner));
}
double calcLW(Parament param)
{
double ret=0.0;
for(int i=0;i<dataSet.size();i++)
{
double h=sigmoid(param,dataSet[i]);
ret+=(dataSet[i].y*log(h))+(1-dataSet[i].y)*log(1-h);
}
return ret;
}
void gradient(Parament ¶m,int iter)
{
/*batch
for(int i=0;i<param.w.size();i++)
{
double ret=0.0;
for(int j=0;j<dataSet.size();j++)
{
double ALPHA=(double)0.1/(iter+j+1)+0.1;
ret+=ALPHA*(dataSet[j].y-sigmoid(param,dataSet[j]))*dataSet[j].feature[i];
}
param.w[i]+=ret;
}
for(int i=0;i<dataSet.size();i++) ret+=alpha*(dataSet[i].y-sigmoid(param,dataSet[i]));
*/
//random
for(int j=0;j<dataSet.size();j++)
{
double ret=0.0,h=sigmoid(param,dataSet[j]);
double ALPHA=(double)0.1/(iter+j+1)+0.1;
for(int i=0;i<param.w.size();i++)
param.w[i]+=ALPHA*(dataSet[j].y-h)*dataSet[j].feature[i];
param.b+=alpha*(dataSet[j].y-h);
}
}
bool samewb(Parament p1,Parament p2)
{
for(int i=0;i<p1.w.size();i++)
if(fabs(p2.w[i]-p1.w[i])>delta) return false;
if(fabs(p2.b-p1.b)>delta) return false;
return true;
}
void classify()
{
ifstream fin("testdata.txt");
int id,fea,cls;
string line;
while(getline(cin,line))
{
stringstream sin(line);
vector<int> feature;
sin>>id;
while(sin>>fea) feature.push_back(fea);
cls=feature.back();feature.pop_back();
double p1=sigmoid(parament,Data(feature,cls)),p0=1-p1;
cout<<"id:"<<id<<" origin:"<<cls<<" classify:";
if(p1>=p0) cout<<" 1"<<endl;
else cout<<" 0"<<endl;
}
}
void mainProcess()
{
double objLW=calcLW(parament),newLW;
Parament old=parament;
int iter=0;
gradient(parament,iter);
newLW=calcLW(parament);
while(fabs(newLW-objLW)>delta||!samewb(old,parament))
{
objLW=newLW;
old=parament;
gradient(parament,iter);
newLW=calcLW(parament);
iter++;
if(iter%5==0) cout<<"iter: "<<iter<<" target value: "<<newLW<<endl;
}
cout<<endl<<endl;
}
int main()
{
read();
mainProcess();
classify();
}
#include "cstdio"
#include "iostream"
#include "fstream"
#include "vector"
#include "sstream"
#include "string"
#include "math.h"
using namespace std;
#define N 500
#define delta 0.0001
#define alpha 0.1
#define cin fin
struct Data
{
vector<int> feature;
int y;
Data(vector<int> feature,int y):feature(feature),y(y) {}
};
struct Parament
{
vector<double> w;
double b;
Parament() {}
Parament(vector<double> w,double b):w(w),b(b) {}
};
vector<Data> dataSet;
Parament parament;
void read()
{
ifstream fin("traindata.txt");
int id,fea,cls,cnt=0;
string line;
while(getline(cin,line))
{
stringstream sin(line);
vector<int> feature;
sin>>id;
while(sin>>fea) feature.push_back(fea);
cls=feature.back();feature.pop_back();
dataSet.push_back(Data(feature,cls));
}
parament=Parament(vector<double>(dataSet[0].feature.size(),0.0),0.0);
}
double calcInner(Parament param,Data data)
{
double ret=0.0;
for(int i=0;i<data.feature.size();i++) ret+=(param.w[i]*data.feature[i]);
return ret+param.b;
}
double sigmoid(Parament param,Data data)
{
double inner=calcInner(param,data);
return exp(inner)/(1+exp(inner));
}
double calcLW(Parament param)
{
double ret=0.0;
for(int i=0;i<dataSet.size();i++)
{
double h=sigmoid(param,dataSet[i]);
ret+=(dataSet[i].y*log(h))+(1-dataSet[i].y)*log(1-h);
}
return ret;
}
void gradient(Parament ¶m,int iter)
{
/*batch
for(int i=0;i<param.w.size();i++)
{
double ret=0.0;
for(int j=0;j<dataSet.size();j++)
{
double ALPHA=(double)0.1/(iter+j+1)+0.1;
ret+=ALPHA*(dataSet[j].y-sigmoid(param,dataSet[j]))*dataSet[j].feature[i];
}
param.w[i]+=ret;
}
for(int i=0;i<dataSet.size();i++) ret+=alpha*(dataSet[i].y-sigmoid(param,dataSet[i]));
*/
//random
for(int j=0;j<dataSet.size();j++)
{
double ret=0.0,h=sigmoid(param,dataSet[j]);
double ALPHA=(double)0.1/(iter+j+1)+0.1;
for(int i=0;i<param.w.size();i++)
param.w[i]+=ALPHA*(dataSet[j].y-h)*dataSet[j].feature[i];
param.b+=alpha*(dataSet[j].y-h);
}
}
bool samewb(Parament p1,Parament p2)
{
for(int i=0;i<p1.w.size();i++)
if(fabs(p2.w[i]-p1.w[i])>delta) return false;
if(fabs(p2.b-p1.b)>delta) return false;
return true;
}
void classify()
{
ifstream fin("testdata.txt");
int id,fea,cls;
string line;
while(getline(cin,line))
{
stringstream sin(line);
vector<int> feature;
sin>>id;
while(sin>>fea) feature.push_back(fea);
cls=feature.back();feature.pop_back();
double p1=sigmoid(parament,Data(feature,cls)),p0=1-p1;
cout<<"id:"<<id<<" origin:"<<cls<<" classify:";
if(p1>=p0) cout<<" 1"<<endl;
else cout<<" 0"<<endl;
}
}
void mainProcess()
{
double objLW=calcLW(parament),newLW;
Parament old=parament;
int iter=0;
gradient(parament,iter);
newLW=calcLW(parament);
while(fabs(newLW-objLW)>delta||!samewb(old,parament))
{
objLW=newLW;
old=parament;
gradient(parament,iter);
newLW=calcLW(parament);
iter++;
if(iter%5==0) cout<<"iter: "<<iter<<" target value: "<<newLW<<endl;
}
cout<<endl<<endl;
}
int main()
{
read();
mainProcess();
classify();
}