树定义及遍历

1、定义树

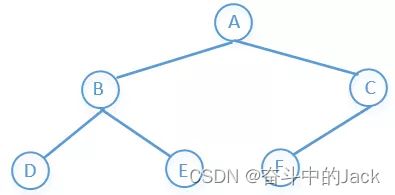
可以参考链表，链表遍历不方便，如果单链表有多个next指针，则就形成了树。

Java:

public class TreeNode {
    int val;
    TreeNode left, right;
    TreeNode(int val) { 
        this.val = val; 
        this.left = null;
        this.right = null;
    }
}

Python：

class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left, self.right = None, None

C++：

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(null), right(null) {}
};

C:

struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};

 2、树的遍历

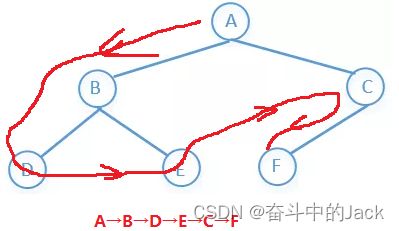
• 前序遍历：根节点→左子树→右子树

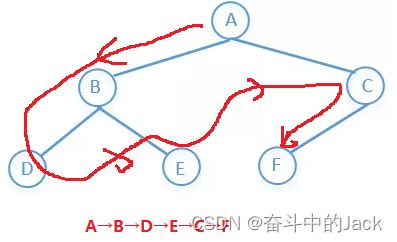
• 中序遍历：左子树→根节点→右子树

• 后序遍历：左子树→右子树→根节点

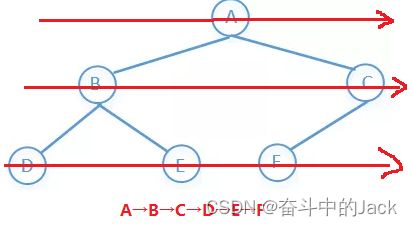
• BFS（广度优先搜索）：先访问上一层，在访问下一层，一层一层的往下访问

• DFS（深度优先搜索）：先访根节点，然后左结点，一直往下，直到最左结点没有子节点的时候然后往上退一步到父节点，然后父节点的右子节点在重复上面步骤……

代码：

1）Python前序、中序、后序遍历：

def preorder(self, root):
    if root:
        self.traverse_path.append(root.val);
        self.preorder(root.left);
        self.preorder(root.right);

def inorder(self, root):
    if root:
        self.preorder(root.left);
        self.traverse_path.append(root.val);
        self.preorder(root.right);

def postorder(self, root):
    if root:
        self.preorder(root.left);
        self.preorder(root.right);
        self.traverse_path.append(root.val);

2）Java遍历：

前序遍历：

// 递归
public static void preOrder(TreeNode tree) {
    if (tree == null)
 return;
    System.out.printf(tree.val + "");
    preOrder(tree.left);
    preOrder(tree.right);
}
// 非递归
public static void preOrder(TreeNode tree) {
    if (tree == null) return;
    Stack q1 = new Stack<>();
    q1.push(tree);//压栈
    while (!q1.empty()) {
        TreeNode t1 = q1.pop();//出栈
        System.out.println(t1.val);
        if (t1.right != null) {
            q1.push(t1.right);
        }
        if (t1.left != null) {
            q1.push(t1.left);
        }
    }
}

中序遍历：

// 递归
public static void inOrder(TreeNode node) {
    if (node == null)  return;
    inOrder(node.left);
    System.out.println(node.val);
    inOrder(node.right);
}
// 非递归
public static void inOrder(TreeNode tree) {
    Stack stack = new Stack<>();
    while (tree != null || !stack.isEmpty()) {
        while (tree != null) {
            stack.push(tree);
            tree = tree.left;
        }
        if (!stack.isEmpty()) {
            tree = stack.pop();
            System.out.println(tree.val);
            tree = tree.right;
        }
    }
}

后序遍历：

// 递归
public static void postOrder(TreeNode tree) {
    if (tree == null) return;
    postOrder(tree.left);
    postOrder(tree.right);
    System.out.println(tree.val);
}
// 非递归
public static void postOrder(TreeNode tree) {
    if (tree == null)
        return;
    Stack s1 = new Stack<>();
    Stack s2 = new Stack<>();
    s1.push(tree);
    while (!s1.isEmpty()) {
        tree = s1.pop();
        s2.push(tree);
        if (tree.left != null) {
            s1.push(tree.left);
        }
        if (tree.right != null) {
            s1.push(tree.right);
        }
    }
    while (!s2.isEmpty()) {
        System.out.print(s2.pop().val + " ");
    }
}

public static void postOrder(TreeNode tree) {
    if (tree == null)
        return;
    Stack stack = new Stack<>();
    stack.push(tree);
    TreeNode c;
    while (!stack.isEmpty()) {
        c = stack.peek();
        if (c.left != null && tree != c.left && tree != c.right) {
            stack.push(c.left);
        } else if (c.right != null && tree != c.right) {
            stack.push(c.right);
        } else {
            System.out.print(stack.pop().val + " ");
            tree = c;
        }
    }
}

BFS（广度优先搜索）：

// 递归
public static void levelOrder(TreeNode tree) {
    int depth = depth(tree);
    for (int level = 0; level < depth; level++) {
        printLevel(tree, level);
    }
}

private static int depth(TreeNode tree) {
    if (tree == null) return 0;
    int leftDepth = depth(tree.left);
    int rightDepth = depth(tree.right);
    return Math.max(leftDepth, rightDepth) + 1;
}

private static void printLevel(TreeNode tree, int level) {
    if (tree == null) return;
    if (level == 0) {
        System.out.print(" " + tree.val);
    } else {
        printLevel(tree.left, level - 1);
        printLevel(tree.right, level - 1);
    }
}

// 非递归
public static void levelOrder1(TreeNode tree) {
    if (tree == null) return;
    LinkedList list = new LinkedList<>(); // 链表，可以把它看做队列
    list.add(tree); // 相当于把数据加入到队列尾部
    while (!list.isEmpty()) {
        TreeNode node = list.poll(); // poll方法相当于移除队列头部的元素
        System.out.println(node.val);
        if (node.left != null) list.add(node.left);
        if (node.right != null) list.add(node.right);
    }
}

// 结果存放到list中
public static List> levelOrder2(TreeNode tree) {
    if (tree == null)
        return null;
    List> list = new ArrayList<>();
    bfs(tree, 0, list);
    return list;
}

private static void bfs(TreeNode tree, int level, List> list) {
    if (tree == null)
        return;
    if (level >= list.size()) {
        List subList = new ArrayList<>();
        subList.add(tree.val);
        list.add(subList);
    } else {
        list.get(level).add(tree.val);
    }
    bfs(tree.left, level + 1, list);
    bfs(tree.right, level + 1, list);
}

DFS（深度优先搜索）：

// 递归
public static void treeDFS(TreeNode root) {
    if (root == null) return;
    System.out.println(root.val);
    treeDFS(root.left);
    treeDFS(root.right);
}

// 非递归
public static void treeDFS1(TreeNode root) {
    Stack stack = new Stack<>();
    stack.add(root);
    while (!stack.empty()) {
        TreeNode node = stack.pop();
        System.out.println(node.val);
        if (node.right != null) {
            stack.push(node.right);
        }
        if (node.left != null) {
            stack.push(node.left);
        }
    }
}