每天刷两道题——第十一天
1.1滑动窗口最大值
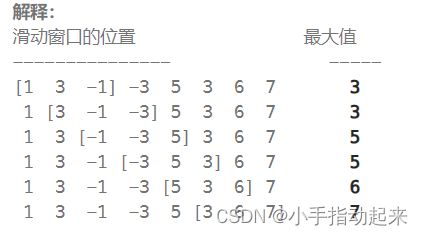
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值 。
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
优先队列
优先队列具有队列的所有特性,包括队列的基本操作,只是在这基础上添加了内部的一个排序,它本质是一个堆实现的。
在优先队列中,元素被赋予优先级。当访问元素时,具有最高优先级的元素最先删除。优先队列具有最高级先出,他和队列不同的就在于我们可以自定义其中数据的优先级,让优先级高的排在队列前面,优先出队。
python的heapq堆
堆是一个二叉树,有两种堆,最大堆与最小堆。 heapq库中的堆默认是最小堆。
1.最小堆,树中各个父节点的值总是小于或等于任何一个子节点的值。
2.最大堆,树中各个父节点的值总是大于或等于任何一个子节点的值。
import heapq
q=heapq.heapify([3,6,4,1]) #将列表转化为堆
heapq.heappush(q,item) #往堆q里面添加元素item
heapq.heappop(q) #删除q中顶部元素
heapq.heapreplace(q,100) #删除顶部元素,加入新值100
#比较77和q中顶部元素,77如果大,删除并返回第一个元素,如果小,返回77,原堆不变
heapq.heappushpop(q,77)
heapq.nlargest(n,q/[3,6,4,1]) #返回堆中最大的前n个
heapq.nsmallest(n,q/[3,6,4,1]) #返回堆中最小的前n个
代码
返回最大值,所以优先级采用负数
def maxSlidingWindow(self,nums,k):
n=len(nums)
#heapq默认为小根堆,我们要找最大值,所以使用-nums[i]为优先级
#-nums[i]为优先级 i为数据下标作为数据传入,前k个数据
q=[(-nums[i],i) for i in range(k)]
heapq.heapify(q) #将列表转化为堆
res=[-q[0][0]] #q[0]=(-3,-1) -q[0][0]=3 第一个滑动窗口的最大值
for i in range(k,n):
heapq.heappush(q,(-nums[i],i)) #添加新元素
#如果数据出现在滑动窗口的左侧将其从堆中删除
while q[0][1]<=i-k: #i是滑动窗口的右侧,i-k是滑动窗口的左侧
heapq.heappop(q)
res.append(-q[0][0]) #存储栈顶的元素
return res
1.2最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
输入:s = “ADOBECODEBANC”, t = “ABC”
输出:“BANC”
解释:最小覆盖子串 “BANC” 包含来自字符串 t 的 ‘A’、‘B’ 和 ‘C’。
枚举
for i,item in enumerate([2,3,4]):
print(i,item)
0 2
1 3
2 4
for i,item in enumerate([2,3,4],start=10):
print(i,item)
10 2
11 3
12 4
代码
def minWindow(self, s: str, t: str) -> str:
need = collections.defaultdict(int)
for c in t:
need[c] += 1
needCnt = len(t)
i = 0 # 记录起始位置
res = (0, float('inf')) # 用两个元素,方便之后记录起终点
# 三步骤:
# 1. 增加右边界使滑窗包含t
for j, c in enumerate(s):
if need[c] > 0:
needCnt -= 1
need[c] -= 1 # 这行放在外面不可以,看19行 need[c] == 0
# 2. 收缩左边界直到无法再去掉元素 !注意,处理的是i
if needCnt == 0: #此时已经包含了t所需的所有元素
while True:
c = s[i]
if need[c] == 0: # 表示再去掉就不行了(need>0)
break
else:
need[c] += 1
i += 1
if j - i < res[1] - res[0]: # 这里是否减一都可以,只要每次都是这样算的就行,反正最后也是输出子串而非长度
res = (i, j)
# 3. i多增加一个位置,准备开始下一次循环(注意这步是在 needCnt == 0里面进行的 )
need[s[i]] += 1
needCnt += 1 # 由于 移动前i这个位置 一定是所需的字母,因此NeedCnt才需要+1
i += 1
return "" if res[1] > len(s) else s[res[0]: res[1] + 1]
参考代码
参考博客
参考博客1
参考博客2