搜索算法专题

1. 深度优先搜索(DFS)

在搜索到一个新的节点时，立即对该新节点进行遍历；因此遍历需要用先入后出的栈来实现，也可以通过与栈等价的递归来实现。对于树结构而言，由于总是对新节点调用遍历，因此看起来是向着“深”的方向前进。
DFS 也可以用来检测环路：记录每个遍历过的节点的父节点，若一个节点被再次遍历且父节点不同，则说明有环。我们也可以用之后会讲到的 拓扑排序 判断是否有环路，若最后存在入度不为零的点，则说明有环。

有时我们可能会需要对已经搜索过的节点进行标记，以防止在遍历时重复搜索某个节点，这
种做法叫做状态记录或记忆化（memoization）。

例题

1.1 岛屿的最大面积

题目描述：
给定一个二维的 0-1 矩阵，其中 0 表示海洋，1 表示陆地。单独的或相邻的陆地可以形成岛
屿，每个格子只与其上下左右四个格子相邻。求最大的岛屿面积。

解题思路：

def maxAreaOfIsland(self, grid) -> int:
	if not grid or len(grid[0])==0:return 0
	maxArea = 0
	for i in range(len(grid)):
		for j in range(len(grif[0])):
			if grid[i][j]==1:
				stack = [(i,j)]
				grid[i][j] = 0
				locaArea = 1
				while stack:
					x,y = stack.pop()
					for x, y in [(x-1, y), (x+1, y), (x, y-1), (x, y+1)]:
                        if 0<=x<len(grid) and 0<=y<len(grid[0]) and grid[x][y]==1:
							stack.append((x,y))
							grid[x][y] = 0
							localArea+=1
				maxArea = max(maxArea,localArea)
				
	return maxArea


# 递归法
def dfs(x,y):
	if grid[x][y]==0:return 0
	grid[x][y] = 0
	area = 1
	for x, y in [(x-1, y), (x+1, y), (x, y-1), (x, y+1)]:
		if 0<=x<len(grid) and 0<=y<len(grid[0]) :
			area+=dfs(x,y)
	return area


def maxAreaOfIsland(self, grid) -> int:
	if not grid or len(grid[0])==0:return 0
		maxArea = 0
		for i in range(len(grid)):
			for j in range(len(grif[0])):
				if grid[i][j]==1:
					maxArea = max(maxArea,dfs(i,j))	
	return maxArea

1.2 省份数量（547）

题目描述：
有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

解题思路：
遍历所有城市，对于每个城市，如果该城市尚未被访问过，则从该城市开始深度优先搜索，通过矩阵 $isConnected$ 得到与该城市直接相连的城市有哪些，这些城市和该城市属于同一个连通分量，然后对这些城市继续深度优先搜索，直到同一个连通分量的所有城市都被访问到，即可得到一个省份。遍历完全部城市以后，即可得到连通分量的总数，即省份的总数。

def findCircleNum(self, isConnected: List[List[int]]) -> int:
        def dfs(i):
            for j in range(cities):
                if isConnected[i][j] == 1 and j not in visited:
                    visited.add(j)
                    dfs(j)
        
        cities = len(isConnected)
        visited = set()
        provinces = 0

        for i in range(cities):
            if i not in visited:
                dfs(i)
                provinces += 1
        
        return provinces

1.3 太平洋大西洋水流问题（417）

题目描述：
给定一个二维的非负整数矩阵，每个位置的值表示海拔高度。假设左边和上边是太平洋，右
边和下边是大西洋，求从哪些位置向下流水，可以流到太平洋和大西洋。水只能从海拔高的位置
流到海拔低或相同的位置。

解题思路：
虽然题目要求的是满足向下流能到达两个大洋的位置，如果我们对所有的位置进行搜索，那
么在不剪枝的情况下复杂度会很高。因此我们可以反过来想，从两个大洋开始向上流，这样我们
只需要对矩形四条边进行搜索。搜索完成后，只需遍历一遍矩阵，满足条件的位置即为两个大洋
向上流都能到达的位置。
简单来说这题起点（答案）不明确但是终点（边界）明确，所以从边界出发能方便地找到答案

def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
        res = []
        m = len(heights)
        n = len(heights[0])
        
        pacific = [(0,i) for i in range(n)]+[(i,0) for i in range(1,m)] # 太平洋
        atlantic = [(m-1,i) for i in range(n)]+[(i,n-1) for i in range(m-1)] # 大西洋

        def dfs(visited,x,y):
            if (x,y) in visited:
                return 
            visited.add((x,y))
            for nx,ny in ((x, y + 1), (x, y - 1), (x - 1, y), (x + 1, y)):
                if 0<=nx<m and 0<=ny<n and heights[nx][ny] >= heights[x][y]:
                    dfs(visited,nx,ny)

        def search(start):
            visited = set()
            for x,y in start:
                dfs(visited,x,y)
            return visited

        return list(map(list, search(pacific) & search(atlantic)))

2.宽度优先搜索(BFS)

广度优先搜索（breadth-first search，BFS）不同与深度优先搜索，它是 一层层 进行遍历的，因
此需要用先入先出的队列而非先入后出的栈进行遍历。由于是按层次进行遍历，广度优先搜索时
按照“广”的方向进行遍历的，也常常用来处理 最短路径 等问题。

考虑如下一颗简单的树。我们从 1 号节点开始遍历，假如遍历顺序是从左子节点到右子节点，
那么按照优先向着“广”的方向前进的策略，队列顶端的元素变化过程为 [1]->[2->3]->[4]，其中
方括号代表每一层的元素。

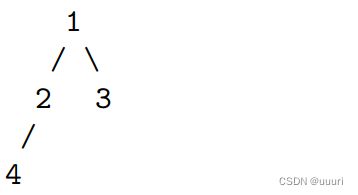
例题

2.1 最短的桥（934）

题目描述：
给定一个二维 0-1 矩阵，其中 1 表示陆地，0 表示海洋，每个位置与上下左右相连。已知矩
阵中有且只有两个岛屿，求最少要填海造陆多少个位置才可以将两个岛屿相连。

解题思路：
使用的方法非常直接：

1. 找到任意一座岛，BFS 扩展全岛
2. 对找到的岛以多源 BFS 分步拓展，找到另一座岛的最短步数即最短的桥

def shortestBridge(self, grid: List[List[int]]) -> int:
        n = len(grid)
        island = []
        que = collections.deque()
        for i in range(n):
            for j in range(n):
                if grid[i][j]==1:
                    grid[i][j]=2
                    island.append((i,j))
                    que.append((i,j))
                    while que:
                        x,y=que.pop()
                        for nx,ny in [(x-1,y),(x+1,y),(x,y-1),(x,y+1)]:
                            if 0<=nx<n and 0<=ny<n and grid[nx][ny]==1:
                                island.append((nx,ny))
                                grid[nx][ny]=2
                                que.append((nx,ny))
                    break
            if island:break
        step = 0
        q = island
        while True:
            tmp = q
            q = []
            for x, y in tmp:
                for nx, ny in (x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1):
                    if 0 <= nx < n and 0 <= ny < n:
                        if grid[nx][ny] == 1:
                            return step
                        if grid[nx][ny] == 0:
                            grid[nx][ny] = 2
                            q.append((nx, ny))
            step += 1   

2.2 单词接龙（126）

题目描述：
给定一个起始字符串和一个终止字符串，以及一个单词表，求是否可以将起始字符串每次改
一个字符，直到改成终止字符串，且所有中间的修改过程表示的字符串都可以在单词表里找到。
若存在，输出需要修改次数最少的所有更改方式。

解题思路：
把起始字符串、终止字符串、以及单词表里所有的字符串想象成 节点。若两个字符串只有一个字符不同，那么它们相连。

因为题目需要输出修改次数最少的所有修改方式，因此我们可以使用广度优先搜索，求得起始节点到终止节点的最短距离。

一个小技巧：
由于本题起点和终点固定
我们并不是直接从起始节点进行广度优先搜索，直到找到终止节点为止；
而是从起始节点和终止节点分别进行广度优先搜索，每次只延展当前层节点数最少的那一端，这样我们可以减少搜索的总结点数。
举例来说，假设最短距离为 4，如果我们只从一端搜索 4 层，总遍历节点数最多是 1 + 2 + 4 + 8 + 16 = 31；而如果我们从两端各搜索两层，总遍历节点数最多只有 2 × (1 + 2 + 4) = 14。
在搜索结束后，我们还需要通过回溯法来重建所有可能的路径。

def findLadders(beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:
    m = len(wordList)
    # 【特殊情况 1】 endWord 不在列表中
    if endWord not in set(wordList): return []
    
    # is_neighbor(word1, word)=True if word1 and word2 has only one different character
    def is_neighbor(word1, word2):
        cnt_diff = 0
        for i in range(len(word1)):
            if word1[i]!=word2[i]: cnt_diff+=1
            if cnt_diff>1: return False
        return True 

    # 先找出wordlist中每个单词的邻居 （与其只有一个字母不同的单词）
    neighbors = defaultdict(list) # neighbors[i]={与words[i]有一个字母不同的word的下标}
    for i in range(m):
        for j in range(i+1, m):
            if is_neighbor(wordList[i], wordList[j]):
                neighbors[i].append(j)
                neighbors[j].append(i)
    # 找出beginWord的所有邻居
    begins = [i for i in range(m) if is_neighbor(beginWord, wordList[i])]

    # 【特殊情况 2】 beginWord 没有邻居
    if len(begins)==0: return False
    
    # 广度优先找最短路径
    all_paths = []
    que = [[pos] for pos in begins]
    visited = set()
    while que:
        visited_add = set() # 控制某条路径是否访问过
        for _ in range(len(que)): # 对每一层处理
            cur_path = que.pop(0)
            cur_pos = cur_path[-1]
            if wordList[cur_pos]==endWord:
                all_paths.append(cur_path)
            else:
                for next_pos in neighbors[cur_pos]:
                    # 如果在【之前的层】中遍历过 next_pos 则没必要再走
                    # 因为最后即便是到达目标单词 走的路径也更长
                    if next_pos in visited: continue
                    que.append(cur_path+[next_pos])
                    visited_add.add(next_pos)
        # 一层整个遍历完毕 更新visited集合
        visited = visited | visited_add                    
        # 进行完当前层的遍历之后找到了路径 则这一层就是所有的最短路径
        if len(all_paths)>0: break
    
    all_paths_words = [[beginWord]+[wordList[i] for i in l] for l in all_paths]
    return all_paths_words

BFS 模板

BFS 使用队列，把每个还没有搜索到的点依次放入队列，然后再弹出队列的头部元素当做当前遍历点。BFS 总共有两个模板：

1.如果不需要确定当前遍历到了哪一层，BFS 模板如下。

while queue 不空：
    cur = queue.pop()
    for 节点 in cur的所有相邻节点：
        if 该节点有效且未访问过：
            queue.push(该节点)

2.如果要确定当前遍历到了哪一层，BFS 模板如下。

这里增加了 level 表示当前遍历到二叉树中的哪一层了，也可以理解为在一个图中，现在已经走了多少步了。 size 表示在当前遍历层有多少个元素，也就是队列中的元素数，我们把这些元素一次性遍历完，即把当前层的所有元素都向外走了一步。

level = 0
while queue 不空：
    size = queue.size()
    while (size --) {
        cur = queue.pop()
        for 节点 in cur的所有相邻节点：
            if 该节点有效且未被访问过：
                queue.push(该节点)
    }
    level ++;