第五届“传智杯”全国大学生计算机大赛决赛(A-E)题解
A-时效「月岩笠的诅咒」
题目描述
时间节点上发生过的两件事情的时间可被看作两实数 a,b。我们称两个事件满足「周年」关系,当且仅当可以通过执行以下两种操作(可以 0 次)使其相等:
- 将 a 加上 1,即 a←a+1;
- 将 b 加上 1,即 b←b+1。
现在给定实数 a,b,询问它们是否满足「周年」。
输入格式
输入共一行两个实数 a,b。输入保留到小数点后 12 位。
输出格式
输出共一行。如果存在合法方案,输出YES,否则输出NO。
题目大意:
判断两个数的差是否为整数即可
题解:
一开始想直接用如下方法直接判断两数小数部分是否相等的
a=a-(double)(int)a //a开始为double类型
可惜WA了,原因大概是精度问题,那么我们直接用字符串来做就好了
#include
using namespace std;
bool check(string &a, string &b, int idx, int idx2)
{
//两个数没有小数部分,一定成立
if(idx==-1 && idx2==-1)
return true;
//一个数有小数点,一个数没有,观察有小数点的数后面是否全为0
else if (idx == -1 && idx2 != -1)
{
for (int i = 0; i < b.size(); i ++)
if (b[i] != '0')
return false;
return true;
}
else if (idx != -1 && idx == -1)
{
for (int i = 0; i < a.size(); i ++)
if (a[i] != '0')
return false;
return true;
}
//两个数都有小数部分
else
{
if (a == b)
return true;
else
return false;
}
}
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
string a, b;
cin >> a >> b;
int idx = a.find('.'), idx2 = b.find('.');
//只观察小数部分是否相同
if (idx != -1)
a = a.substr(idx + 1);
if (idx2 != -1)
b = b.substr(idx2 + 1);
if (check(a, b, idx, idx2))
cout << "YES";
else
cout << "NO";
return 0;
} B- 不死「火鸟 −凤翼天翔−」
题目描述
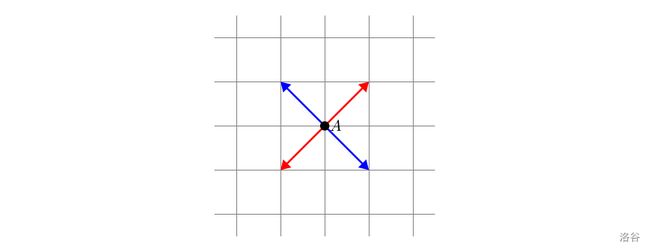
妹红可以操纵火鸟。火鸟可以看作在边长无限大的棋盘上放置着的一枚棋子 A,A 位于 (x1,y1) 处。A 以如下规则移动:
- 在奇数次移动时,A 只能向右上或者左下移动一格,如下图红色箭头;
- 在偶数次移动时,A 只能向右下或者左上移动一格,如下图蓝色箭头。
由于棋盘无限大,因此 x,y 的取值可以为负数。
每一步行动时 A 不能待在原地不移动。现在需要把 A 移动到坐标为 (x2,y2) 的位置,最少要多少步?特别地,若不存在这样的方案,输出 −1。
题解:
先判断什么时候不存在这样的方案,容易观察到,棋子不能直接的走上下左右四个方向,所以设出横纵坐标差的绝对值
int dx=abs(x1-x2),dy=abs(y1-y2)
所以当(dx+dy)为奇数时无解,输出-1
所以当有解的情况下,可以发现
dx,dy都为奇数,或 dx,dy都为偶数
1.当dx,dy都为偶数时
发现第一步第二步无论怎么搭配走法,都只能完成一个维度的移动
所以此时答案就是dx+dy
2.当dx,dy都为奇数时
我们只需要走出第一步就能回到第一种情况
如 A=(2,7),B=(5,2)时
dx=3,dy=5
走出第一步后 A=(3,8)或(1,6)
所以此时答案就是算出新的两点到B的距离+1就行了
#include
#include
using namespace std;
int main()
{
int x1,x2,y1,y2;
cin>>x1>>y1>>x2>>y2;
int dx=abs(x1-x2),dy=abs(y1-y2);
if((dx+dy)%2) //观察发现,当坐标差的和是奇数时一定无解
cout<<-1;
else
{
if(dx%2==0)
cout< C-藤原「灭罪寺院伤」
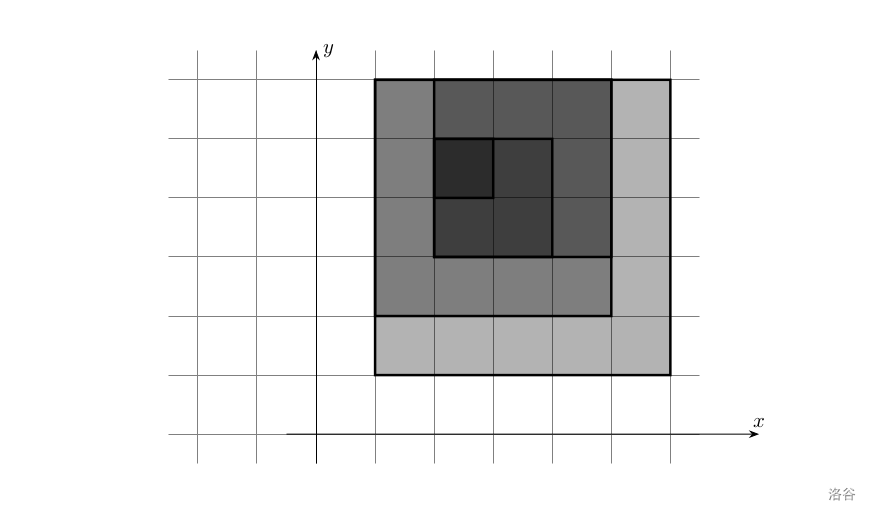
环环相扣的因果报应可看成平面上的 n 个小正方形,它们的边长分别为 1,2,3,⋯,n。初始时,编号较小的正方形被编号较大的正方形完全包含:
为了方便记录正方形的位置,我们取正方形左上角的坐标 (xi,yi) 为正方形的坐标。此时可以唯一确定该正方形。
现在需要将最小的正方形的位置移动到 (xend,yend),移动过程满足:
- 每次最多移动一个正方形,可以往上下左右四个方向之一移动一个单位长度。
- 在移动过程中,需要保证较小正方形会被较大的正方形包含。
请求出最少次数。
题解:
思考后发现,最终的状态一定是所有的小正方形包含了目标点,所以我们可以不用去管中间状态,直接计算初始状态到最终状态的代价
所以我们只要贪心的去求每个正方形到包含目标点的最小距离即可
#include
#include
#include
using namespace std;
const int N=1e5+5;
typedef struct{
int x1,y1;
int x2,y2;
int x3,y3;
}sq;
sq sqr[N];
int main()
{
int n,ex,ey;
cin>>n>>ex>>ey;
//表示出正方形的坐标点
for(int i=1;i<=n;i++)
{
cin>>sqr[i].x1>>sqr[i].y1;
sqr[i].x2=sqr[i].x1+i-1;
sqr[i].y2=sqr[i].y1;
sqr[i].x3=sqr[i].x1;
sqr[i].y3=sqr[i].y1-i+1;
}
long long ans=0;
int dx,dy;
for(int i=1;i<=n;i++)
{
//观察横纵坐标上的关系
//在正方形内则不用计算,
if(ex<=sqr[i].x2 && ex>=sqr[i].x1)
dx=0;
//否则就是到正方形某一条边的最短距离
else
{
dx=min(abs(ex-sqr[i].x1),abs(ex-sqr[i].x2));
}
if(ey<=sqr[i].y1 && ey>=sqr[i].y3)
dy=0;
else
dy=min(abs(ey-sqr[i].y1),abs(ey-sqr[i].y3));
ans+=dx+dy;
}
cout< D-不死「徐福时空」
题目描述
时间的流逝可以抽象成对数字序列进行排序所花费的时间。不同排序策略花费的时间是不同的。这里介绍一种人类探索排序过程中具有里程碑意义的一种排序算法:希尔排序。
希尔排序可以被视为一种对插入排序的优化。为了研究希尔排序的运行效率,我们希望你实现一个简单的希尔排序的过程。在这之前,我们会规范插入排序的具体流程以及评价一个插入排序的过程的「代价」。
插入排序
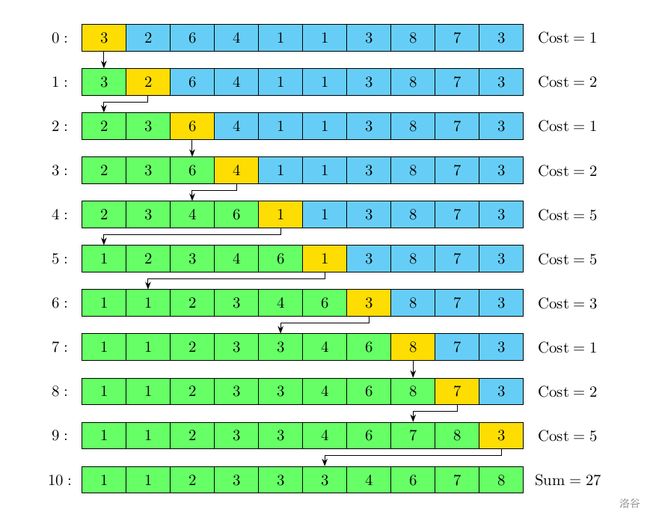
对于一个长度为 n 的数组 a=[a1,a2,⋯,an],插入排序的思想是,从前到后枚举每一个元素,将其插入到正确的位置上去:
如图所示是一个典型的插入排序的过程。在第 i 轮中我们把下标为 i 的元素插入到了排好序的部分中第一个比 ai 大的元素之前。假设 ai 最终被插入到了 bi 位置,那么我们称这一轮的代价为 ∣ai−bi∣+1,整个插入排序的过程的代价就是每一轮的代价之和。
希尔排序
为了减小插入排序的代价,我们引入了希尔排序。希尔排序将整个排序过程分成了若干轮,每一轮会按照一定的间隔把元素分组,对每一组内的元素分别进行排序。在最后一轮,希尔排序会对整个数组进行一次最终的插入排序。
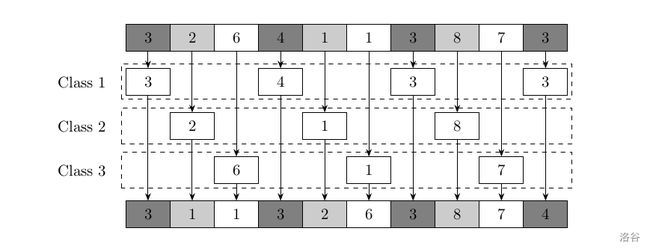
具体的分组方式是,选定一个整数 d,划分为如下组别:
- 下标为 1,1+d,1+2d,⋯ 的元素;
- 下标为 2,2+d,2+2d,⋯ 的元素;
- 下标为 3,3+d,3+2d,⋯ 的元素;
- ……
- 下标为 d,2d,3d,⋯ 的元素。
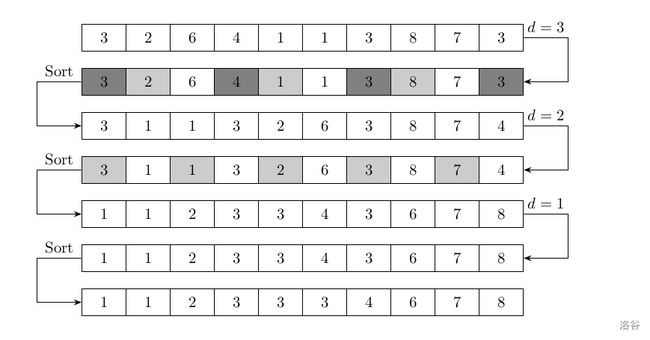
下面是一轮希尔排序的过程。我们选定 d=3。
希尔排序每一轮分别选取 d,并且在最后一轮取 d=1,每一轮都进行这样的排序,最终得到一个有序的数组。
虽然看上去进行了很多轮插入排序,但是最终每一轮插入排序的代价之和可能会远小于对整个数组进行单次插入排序的代价(上述例子中体现得并不明显,可以参考样例 2,3 给出的例子)。
事实上,希尔排序是人类发现的第一个最坏复杂度低于 O(n^2) 的排序算法。例如,当取 d=2k−1, k=⌊log2n⌋,⌊log2n⌋−1,⌊log2n⌋−2,⋯,1 时,整个过程的最坏时间复杂度为 O(n3/2)。
题解
按照希尔排序的规则直接模拟过程进行计算即可,不懂希尔排序的可以先去了解希尔排序,了解后可以秒懂题意,再试着写代码
#include
#include
#include
using namespace std;
const int N=2e5+5;
typedef long long ll;
int nums[N];
void swap(int &a,int &b)
{
ll tmp=a;
a=b;
b=tmp;
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>nums[i];
}
ll ans=0;
while(m--)
{
int d;
cin>>d;
for(int i=1;i<=d;i++)
{
int idx=i;
while(idx<=n)
{
int preid=idx-d;
int nowid=idx;
//一定要先判断前一个的索引是否大于0,判断条件不能交换,否则将产生段错误
while(preid>0 && nums[nowid] E-P9207 灭罪「正直者之死」
题目描述
有一台计算器,使用 k 位的带符号整型来对数字进行存储。也就是说,一个变量能够表示的范围是 [−2k−1,2k−1)。现在我们希望使用该计算器计算一系列数 a1,a2,⋯,an 的和。计算的伪代码如下:
由于奇怪的特性,如果两个变量在相加时得到的结果在 [−2k−1,2k−1) 之外,即发生了溢出,那么这台计算器就会卡死,再也无法进行计算了。
为了防止这样的事情发生,一个变通的方法是更改 ai 的排列顺序。容易发现这样不会改变计算出的和的值。
不过,可能不存在一种方案,使得计算出这 n 个数并且计算机不爆炸。但我们还是希望,计算出尽量多的数字的和。
题目大意
有一个k位的带符号整型(类似于int,long long)计算n个有正有负的数,问最多能计算多少个使得该整型不会溢出
题解:
一开始的思路是维护一个sum(初始为0)
若sum<=0,sum加上一个正数
若sum>0,sum加上一个负数
然后我们再来敲定一些细节
我们肯定是希望sum的绝对值是更小的,所以我们每次加的数应该也是绝对值最小的数
如果sum<=0却没有正数加了我们只能去加负数了,sum>0时同样如此
中途本来还考虑过sum<=0加上一个正数反而溢出的情况,但是数据说了ai本身不会溢出,所以也可以不考虑,那我们只需要将所有的数分成正数和负数两组,然后再按绝对值从小到大排序,最后按照上面的思路做就行了
#include
#include
using namespace std;
const int N=505;
int nums[N];
int pnum[N];
int nnum[N];
bool cmp(int a,int b)
{
return abs(a)>n>>k;
for(int i=1;i<=n;i++)
{
cin>>nums[i];
}
sort(nums+1,nums+n+1,cmp);
int pedge=1,nedge;
for(int i=2;i<=k;i++)
{
pedge*=2;
}
nedge=pedge*(-1);
pedge-=1;
int sum=0;
int pid=1,nid=1;
for(int i=1;i<=n;i++)
{
if(nums[i]>=0)
{
pnum[pid++]=nums[i];
}
else
{
nnum[nid++]=nums[i];
}
}
int pi=1,ni=1;
while(sum>=nedge && sum<=pedge)
{
if(sum<0)
{
if(pi=0)
{
if(nipedge)
ans--;
cout<