【leetcode】329 矩阵中的最长递增路径(动态规划)
https://leetcode-cn.com/problems/longest-increasing-path-in-a-matrix/
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)
示例 1:
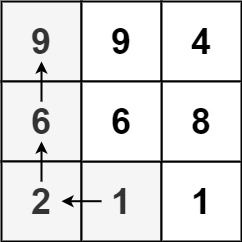
输入:matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出:4
解释:最长递增路径为 [1, 2, 6, 9]。
示例 2:
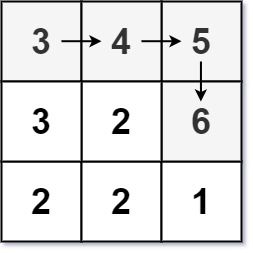
输入:matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出:4
解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
示例 3:
输入:matrix = [[1]]
输出:1
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
0 <= matrix[i][j] <= 231 - 1
思路
动态规划思路,用二维数组dp记忆位置(i,j)的最大递增序列长度。
dp[x][y] = max(dp[x][y], dfs(matrix,x+dx,y+dy,dp)) if matrix[x][y] > matrx[x+dx][y+dy]
利用比当前元素大且已经被计算过的邻居元素进行计算!确保从一个方向访问(不管最终的序列总体是从上到下的还是从下到上的递增,不会重复计算)。
关键在于dfs:能够无重复地计算最大长度,注意如果计算过的节点,应该直接返回。
所有的路径一定是以图中某个点为起点,然后向四周延展,那么我们可以遍历每一个点,以这个点为起点,记录这个路径最长能达到多长,即可遍历完图中所有的路径,然后需要解决的是如何求以这个节点出发的最长路径,路径的延展无非是向四个方向进行,那么我在判定当前这个节点最长路径时,只需要前确定与这个节点相邻的四个节点中最长路径即可,然后这个最长路径加1即为当前节点出发的最长路径,OK,至此,此题的思路应该就比较明晰了,函数的返回值肯定是设计为当前节点的最长路径值。由于图的遍历是近乎暴力解法,对其中一个节点遍历时,又会把四周节点的路径值重复求一遍,这个会存在大量的重复计算,因此可以借助记忆数组,避免重复计算。
function dfs(matrix, row, col, dp) {
if (dp[row][col]) {
//该位置有值,即该位置四个方向走过了,不用再走了
return dp[row][col];
}
// 上下左右四个方向
const dirs = [
[-1, 0],
[1, 0],
[0, -1],
[0, 1],
];
dp[row][col] = 1; // 该坐标访问,长度至少为1,表示走的次数
for (let i = 0; i < dirs.length; i++) {
//每个元素都可以走4个方向
let dir = dirs[i];
let dx = dir[0];
let dy = dir[1];
if (
row + dx < 0 ||
row + dx >= matrix.length ||
col + dy < 0 ||
col + dy >= matrix[0].length
) {
continue; // 坐标出界-不能移动到边界外,若是该方向走后超出边界即该方向不能走
}
if (matrix[row][col] <= matrix[row + dx][col + dy]) {
//因为查找递增序列:小-》到,倒着走(递减)这样最后走的次数会大,统计前面走过的次数
continue;
}
dp[row][col] = Math.max(
dp[row][col],
dfs(matrix, row + dx, col + dy, dp) + 1 //可以走的方向:该位置的次数是他下面可以走的位置次数+1
); // 回溯
}
return dp[row][col];
}
function findMaxLen(matrix) {
if (!Array.isArray(matrix) || !Array.isArray(matrix[0])) {
return 0;
}
const rows = matrix.length;
const cols = matrix[0].length;
const dp = [];
for (let i = 0; i < rows; i++) {
let arr = [];
for (let j = 0; j < cols; j++) {
arr.push(0);
}
dp.push(arr);
}
let maxLen = 0;
for (let i = 0; i < rows; i++) {
for (let j = 0; j < cols; j++) {
maxLen = Math.max(maxLen, dfs(matrix, i, j, dp));
}
}
// console.log(dp);
return maxLen;
}
var nums = [
[9, 9, 4],
[6, 6, 8],
[2, 1, 1],
]; //4:最长递增路径为 [1, 2, 6, 9]。
var nums1 = [
[3, 4, 5],
[3, 2, 6],
[2, 2, 1],
]; //4:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
var nums2 = [[1]];
console.log(findMaxLen(nums));
console.log(findMaxLen(nums1));
console.log(findMaxLen(nums2));分析代码:以上面 nums数组为例,拆分for循环
1)i=0,j=0:
maxLen = Math.max(maxLen, dfs(matrix, 0, 0, dp));
console.log(maxLen, dp);如上即从i=0j=0的9开始走,按每个位置都可以走4个方向,那么该9走的路线:9-6-2-1,记录走的最长路径,只要走过就是1,那么他递增走的位数上也递增+1,即位置走过信息为4-》3-》2-》1
2)i=0,j=1:
maxLen = Math.max(maxLen, dfs(matrix, 0, 1, dp));
console.log(maxLen, dp);如上:从i=0,j=1的9开始走,两条路可以走9-》4和9-》6-》1,那么9的路线最大就是3,所以是3-》1和3-》2-》1
3)i=0,j=2:
maxLen = Math.max(maxLen, dfs(matrix, 0, 2, dp));
console.log(maxLen, dp);如上:从i=0,j=2的4开始走,4的位置上已经有位置信息,说明该位置已经尝试过4个方向上走,所以不用再走了,直接返回位置上的信息就是其能途径的步数。
i=1,j=0和j=1同理,位置上已经有信息不用在尝试走了
4)i=1,j=2:
maxLen = Math.max(maxLen, dfs(matrix, 1, 2, dp));
console.log(maxLen, dp);如上:从i=1,j=2的8开始走,8可以走的路径:8-》4和8-》6-》1,所以8的位置上信息是3,最长可以走3步。
5)i=2,j=0/1/2:
maxLen = Math.max(maxLen, dfs(matrix, 2, 0, dp));
maxLen = Math.max(maxLen, dfs(matrix, 2, 1, dp));
maxLen = Math.max(maxLen, dfs(matrix, 2, 2, dp));
console.log(maxLen, dp);因为最后一行上所有的列都走过了,直接返回即可,所以上面就是能走过的最长路径信息。