平衡二叉树(AVL树)图解与代码示例
平衡二叉树(AVL树)图解与代码示例
- 平衡二叉树的定义
- 树的高度
-
- 说法一:从0开始
- 说法二:从1开始
- 我的看法
- 辨识
- 平衡二叉树实现原理
- 二叉树的遍历
-
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
- 代码示例
平衡二叉树的定义
 上图中,左边的二叉树和右边的二叉树都是由相同的元素组成,但明显左边的查找性能要优于右边。右边斜树的查找性能直接退化为链表了。二叉树越平衡,查找性能越好。
上图中,左边的二叉树和右边的二叉树都是由相同的元素组成,但明显左边的查找性能要优于右边。右边斜树的查找性能直接退化为链表了。二叉树越平衡,查找性能越好。
平衡二叉树(Self-Balancing Binary Search Tree或Height-Balanced Binary Search Tree
),是一种二叉排序树,其中每一个节点的左子树和右子树的高度差至多等于1.
有两位俄罗斯数学家在1962年共同发明一种解决平衡二叉树的算法,所以有不少资料中也称这样的平衡二叉树为AVL树。AVL是他们名字的缩写。
我们将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF(Balance Factor)。平衡二叉树上所有结点的平衡因子只可能是-1、0、1。
树的高度
平衡二叉树中结点平衡因子的计算依赖于树的高度(或深度),所以要判断是否是平衡二叉树,先要搞清楚啥是树的深度和高度。关于树的深度和高度怎么算,许多书籍与教材的说法都不太一致,有认为从0开始的,也有认为从1开始的。下面我就将这两种说法都整理一遍。
说法一:从0开始
Robert Sedgewick和Kevin Wayne所著的《算法》第4版中定义:
- 树中结点的深度是它到根结点的最长简单路径边的条数
- 树中结点的高度是它到叶子结点的最长简单路径边的条数
- 树的高度等于所有结点的最大深度(即树的深度)
所以树的深度和高度是相等的,而对结点来说深度和高度不一定相等。
另外规定根结点的深度和叶子结点的高度是0。
| 结点 | 高度 | 深度 |
|---|---|---|
| A | 3 | 0 |
| B | 2 | 1 |
| C | 1 | 1 |
| D | 1 | 2 |
| E | 0 | 2 |
| F | 0 | 2 |
| G | 0 | 3 |
| 树 | 3 | 3 |
说法二:从1开始
《大话数据结构》这本书将根结点的深度定义为1. 如下:
结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层。树中结点的最大层次称为树的深度(Depth)或高度。如下图所示,树的高度为4.

但在此书讲解平衡二叉树的章节里又有与这个定义相矛盾的地方,实在让人费解。其实这本书错误的地方挺多的,所以有时候你看不懂可能不是你自己的问题,最好对照勘误的内容再理解一遍。
还是以上面那个图为例,各结点以及树的高度和深度如下表:
| 结点 | 高度 | 深度 |
|---|---|---|
| A | 4 | 1 |
| B | 3 | 2 |
| C | 2 | 2 |
| D | 2 | 3 |
| E | 1 | 3 |
| F | 1 | 3 |
| G | 1 | 4 |
| 树 | 4 | 4 |
我的看法
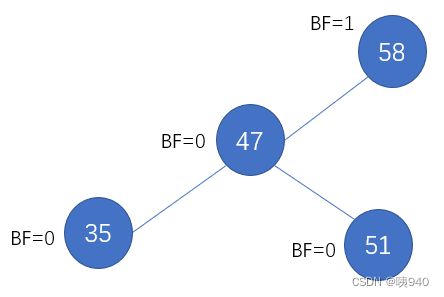
有人说,不管是从0开始还是从1开始,因为平衡因子计算的是差值,所以不影响最终结果。我不认同这个说法。比如说,看下面这棵树:

它到底算不算平衡二叉树?如果我们依据说法一,它的各结点的平衡因子如下:
如果我们按照说法二,它的各结点的平衡因子如下:
关于树高的说法没有统一的规定,我个人更倾向于第二种说法,即从1开始。所以接下来的示例我全部按照说法二来讲解。
辨识
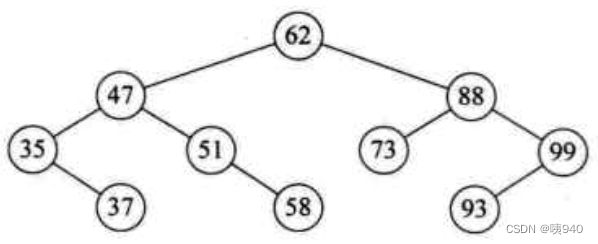
来看几个示例:

上图是不是平衡二叉树?答案是:不是的!这张图出自《大话数据结构》,书里认为它是平衡二叉树,也没说理由,让许多人产生了疑惑,包括我。但我在勘误的内容里看到别人提到了这个有误。再者,如果这个是平衡二叉树,则与此书的很多地方有矛盾。所以它不是平衡二叉树!因为58结点的平衡因子是2!88结点的平衡因子是-2!
再看一个图:

这棵树乍一看是平衡二叉树,但其实不是。平衡二叉树首先要是一棵二叉排序树。图中59比58大,但却在58左边,所以它不是二叉排序树,也就不是平衡二叉树了。
再看一个图:
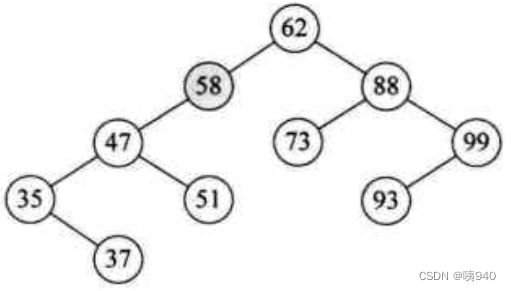
上图也不是平衡二叉树,因为58结点的左子树深度为3,右子树为空,深度为0,左右子树高度差是3.
最后再看一个图:
平衡二叉树实现原理
以距离插入结点最近的,且平衡因子的绝对值大于1的结点为根的子树,我们称为最小不平衡子树。

插入51后二叉树的平衡性遭到破坏。距离51最近的平衡因子的绝对值超过1的结点是58,所以,以58为根结点的树称为最小不平衡子树。
平衡二叉树构建的基本思想就是在构建二叉排序树的过程中,每当插入一个结点时,先检查是否因插入而破坏了树的平衡性,若是,则找出最小不平衡子树。在保持二叉排序树特性的前提下,调整最小不平衡子树中各结点之间的链接关系,进行相应的旋转,使之成为新的平衡子树。
假设现在我们有{3, 2, 1 ,4, 5, 6, 7, 10, 9, 8}这几个元素,依次插入构成平衡二叉树。
当插入1时,整棵树变成了最小不平衡子树,因此需要调整。我们将整棵树右旋(顺时针旋转)。

当插入5时,以3为根结点的树变成了最小不平衡子树,此时将最小不平衡子树左旋(逆时针旋转),这样调整完之后,整棵树又是平衡二叉树了。
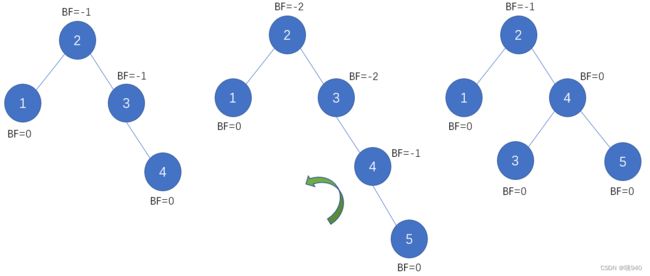
继续添加6,发现根结点2的BF变成了-2,所以我们对根结点进行了左旋,注意,结点3本来是4的左孩子,由于旋转后需要满足二叉排序树的特性,因此它成了结点2的右孩子。(画图太麻烦了,直接用别人的图吧)

当增加结点10时,结构无变化。再增加结点9,此时结点7的BF变成了-2,理论上我们只需要旋转最小不平衡子树7、9、10即可,但是如果左旋转,结点9就成了10的右孩子,这是不符合二叉排序树的特性的哦,此时不能简单的左旋。
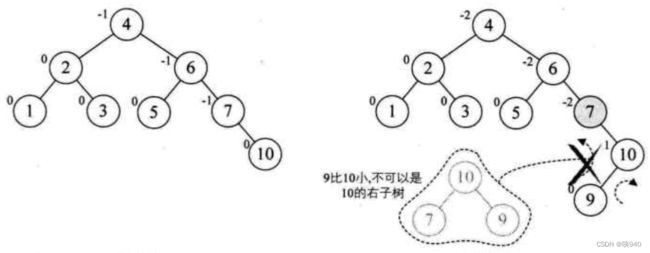
仔细观察,发现结点7的BF是-2,而结点10的BF是1,也就是说,它们俩一正一负,符号并不统一,而前面的几次旋转,无论左旋还是右旋,最小不平衡子树的根结点与它的子结点的平衡因子的符号是相同的。这就是不能直接旋转的关键。
这种情况,只能先将它们的符号统一再说。于是我们先对结点9和10进行右旋,使得结点10成为9的右子树,结点9的BF为-1,此时就与结点7的BF值的符号统一了。这样我们再对最小不平衡子树进行左旋。


接着插入8,情况与刚才类似,结点6的BF是-2,而它的右孩子9的BF是1,因此首先以9为根结点,进行右旋。此时结点6和结点7的符号都是负,再以6为根结点左旋,最终得到最后的平衡二叉树。
对于如何旋转,简单归纳下就是:
- 左旋(逆时针旋转)增加左子树高度,减小右子树高度,使子树根结点平衡因子BF变大
- 右旋(顺时针旋转)增加右子树高度,减小左子树高度,使子树根结点平衡因子BF变小
- 如果是左旋,当根结点右孩子的BF(非0)符号和根结点的BF符号不一致时,需要将根结点右孩子的BF调整到与根结点的BF一致(或调整到0)后才能左旋,也就是要作双旋处理
- 如果是右旋,当根结点左孩子的BF(非0)符号和根结点的BF符号不一致时,需要将根结点左孩子的BF调整到与根结点的BF一致(或调整到0)后才能右旋,也就是要作双旋处理
二叉树的遍历
二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
二叉树的遍历方法一般有前序遍历、中序遍历、后序遍历、层序遍历。
前序遍历
每个初学者都会被前序、中序、后序到底指的是什么顺序搞懵,于是他们想通过看图来直观理解,结果越看越糊涂。听我的,想理解前序、中序、后序,最有效的方法是看代码,比如前序遍历:
/**
* 前序遍历
*/
public void prevOrderTraverse() {
prevOrderTraverse(root);
}
private void prevOrderTraverse(Node c) {
if (c == null)
return;
printlnNode(c); // 把对当前结点的操作放在左、右孩子前面
prevOrderTraverse(c.left);
prevOrderTraverse(c.right);
}
private void printlnNode(Node n) {
System.out.println("key: " + n.key + ", value: " + n.value + ", isLeft: " + n.isLeft);
}
把对当前结点的操作放在左、右孩子前面,就是前序遍历,就这么简单!对应的遍历顺序如下图所示(结合递归来理解非常的直观):
中序遍历
/**
* 中序遍历
*/
public void inOrderTraverse() {
inOrderTraverse(root);
}
private void inOrderTraverse(Node c) {
if (c == null)
return;
inOrderTraverse(c.left);
printlnNode(c); // 把对当前结点的操作放在左孩子和右孩子中间
inOrderTraverse(c.right);
}
中序遍历有个特点,即它是按从小到大的顺序遍历结点的。
后序遍历
/**
* 后序遍历
*/
public void postOrderTraverse() {
postOrderTraverse(root);
}
private void postOrderTraverse(Node c) {
if (c == null)
return;
postOrderTraverse(c.left);
postOrderTraverse(c.right);
printlnNode(c); // 把对当前结点的操作放在左、右孩子后面
}
层序遍历
/**
* 层序遍历
*/
public void levelOrderTraverse() {
if (root == null)
return;
Queue<Node> queue = new LinkedList<>();
queue.add(root);
queue.add(null); // 占位符,表示一层结束
while (!queue.isEmpty()) {
Node c = queue.poll();
if (c != null) {
printNode(c);
if (c.left != null)
queue.add(c.left);
if (c.right != null)
queue.add(c.right);
} else {
System.out.println();
if (queue.isEmpty()) // 不加这个判断会死循环
break;
else
queue.add(null); // 占位符,表示一层结束
}
}
}
private void printNode(Node n) {
System.out.print("key: " + n.key + ", isLeft: " + n.isLeft + " | ");
}
和前序、中序、后序遍历不同的是,层序遍历完全可以对照图来理解。
代码示例
package org.example.demo.tree;
import java.util.LinkedList;
import java.util.Queue;
/**
* 平衡二叉树(Self-Balancing Binary Search Tree或Height-Balanced Binary Search Tree或AVL树)
*/
public class AVLTree {
private static final int HOLDER_FLAG_HAVE = 0;
private static final int HOLDER_FLAG_NON = -1;
/**
* 求结点n的平衡因子
* @param n 结点
* @return 平衡因子
*/
public static int bf(Node n) {
return height(n.left) - height(n.right);
}
/**
* 求以n为根结点的树高
* @param n 结点
* @return 树的高度
*/
public static int height(Node n) {
if (n == null)
return 0;
return Math.max(height(n.left), height(n.right)) + 1;
}
static class Node {
/**
* 平衡因子-左子树高
*/
private static final int BF_LH = 1;
/**
* 平衡因子-左右子树一样高
*/
//private static final int BF_EH = 0;
/**
* 平衡因子-右子树高
*/
private static final int BF_RH = -1;
/**
* 用于排序和查找的关键字,为了演示方便使用int
*/
private int key;
/**
* 结点存储的数据,为了演示方便使用int
*/
private final int value;
private Node left, right, parent;
private Boolean isLeft;
public Node(int key, int value) {
this.key = key;
this.value = value;
}
public boolean isRoot() {
return isLeft == null;
}
}
/**
* 树的结点个数
*/
private int size;
/**
* 树的根结点
*/
private Node root;
/**
* 用于持有最小不平衡子树根结点的引用,data=HOLDER_FLAG_NON表示没有最小不平衡子树
*/
private final Node minSizeNotBalancedTreeRootHolder = new Node(HOLDER_FLAG_NON, -1);
public AVLTree() {}
public AVLTree(Node root) {
this.root = root;
}
/**
* 插入新的数据
* @param key 关键字
* @param value 数据
*/
public void insert(int key, int value) {
insert(new Node(key, value));
}
/**
* 插入新的结点
* @param n 新的结点
*/
private void insert(Node n) {
if (root == null) {
setRoot(n);
size++;
} else {
resetHolder();
insert(root, n);
adjust();
}
}
private void insert(Node p, Node n) {
if (n.key < p.key) {
if (p.left == null) {
n.parent = p;
n.isLeft = Boolean.TRUE;
p.left = n;
size++;
return; // p绝对不可能是最小不平衡子树的根结点,所以这里可以直接返回
} else {
insert(p.left, n);
}
} else if (n.key > p.key) {
if (p.right == null) {
n.parent = p;
n.isLeft = Boolean.FALSE;
p.right = n;
size++;
return; // p绝对不可能是最小不平衡子树的根结点,所以这里可以直接返回
} else {
insert(p.right, n);
}
}
// 递归返回时,可以遍历新插入的结点n到树的根结点root的最短路径上的结点
// 因此,这样求得的第一个bf的绝对值大于等于2的结点即为最小不平衡子树的根结点
minSizeNotBalancedTree(p);
}
/**
* 根据关键字查找数据
* @param key 关键字
* @return 数据
*/
public Integer search(int key) {
return search(root, key);
}
private Integer search(Node c, int key) {
if (c == null)
return null;
if (key == c.key) {
return c.value;
} else if (key > c.key) {
return search(c.right, key);
} else {
return search(c.left, key);
}
}
/**
* 移除结点
* @param key 关键字
*/
public void remove(int key) {
resetHolder();
remove(root, key);
adjust();
}
/**
* 移除结点
* @param c 当前结点(current node)
* @param key 关键字
*/
private void remove(Node c, int key) {
if (c == null)
return;
if (key == c.key) {
if (c.left == null && c.right == null) { // c是叶子结点或者树只有一个结点
removeNoChildNode(c);
minSizeNotBalancedTree2(c.parent);
} else if (c.left != null && c.right == null) { // "独子继承家业"
if (!c.isRoot()) {
if (c.isLeft) {
c.parent.left = c.left;
c.left.parent = c.parent;
} else {
c.parent.right = c.left;
c.left.parent = c.parent;
c.left.isLeft = Boolean.FALSE;
}
} else
setRoot(c.left);
minSizeNotBalancedTree2(c.parent);
} else if (c.left == null && c.right != null) { // "独子继承家业"
if (!c.isRoot()) {
if (c.isLeft) {
c.parent.left = c.right;
c.right.parent = c.parent;
c.right.isLeft = Boolean.TRUE;
} else {
c.parent.right = c.right;
c.right.parent = c.parent;
}
} else
setRoot(c.right);
minSizeNotBalancedTree2(c.parent);
} else
removeTwoChildNode(c);
size--;
} else if (key > c.key) {
remove(c.right, key);
} else {
remove(c.left, key);
}
}
private void removeNoChildNode(Node n) {
if (!n.isRoot()) {
if (n.isLeft)
n.parent.left = null;
else
n.parent.right = null;
} else
root = null;
}
private void removeTwoChildNode(Node n) {
/*
* 二叉树中序遍历是按照值从小到大的顺序遍历的。
* 如果我们以当前结点n作为根结点进行中序遍历,
* 就能找到当前结点的直接前驱结点(左子树中值最大的结点)
* 或者直接后继结点(右子树中值最小的结点)s,
* 将s与n互换位置,然后删除n
*/
// 这里我们使用直接前驱结点作为s
Node s = findPrevSuccessor(n);
if (s.isLeft) { // 此时s是n的左孩子
s.right = n.right;
if (n.isRoot())
setRoot(s);
else {
if (n.isLeft) {
n.parent.left = s;
s.parent = n.parent;
} else {
n.parent.right = s;
s.parent = n.parent;
s.isLeft = Boolean.FALSE;
}
}
minSizeNotBalancedTree2(s);
} else { // s是n的子孙
// 保存s的属性值
Node d = new Node(0, 0);
// s只可能有左孩子,不可能有右孩子
d.left = s.left;
d.parent = s.parent;
// 将s换到n的位置
s.left = n.left;
s.right = n.right;
if (n.isRoot())
setRoot(s);
else {
if (n.isLeft) {
n.parent.left = s;
s.parent = n.parent;
s.isLeft = Boolean.TRUE;
} else {
n.parent.right = s;
s.parent = n.parent;
}
}
if (d.left != null) {
d.parent.right = d.left;
d.left.isLeft = Boolean.FALSE;
} else
d.parent.right = null;
minSizeNotBalancedTree2(d.parent);
}
}
private void printlnNode(Node n) {
System.out.println("key: " + n.key + ", value: " + n.value + ", isLeft: " + n.isLeft);
}
private void printNode(Node n) {
System.out.print("key: " + n.key + ", value: " + n.value + ", isLeft: " + n.isLeft + " | ");
}
/**
* 前序遍历
*/
public void prevOrderTraverse() {
prevOrderTraverse(root);
}
private void prevOrderTraverse(Node c) {
if (c == null)
return;
printlnNode(c);
prevOrderTraverse(c.left);
prevOrderTraverse(c.right);
}
/**
* 中序遍历
*/
public void inOrderTraverse() {
inOrderTraverse(root);
}
private void inOrderTraverse(Node c) {
if (c == null)
return;
inOrderTraverse(c.left);
printlnNode(c);
inOrderTraverse(c.right);
}
/**
* 后序遍历
*/
public void postOrderTraverse() {
postOrderTraverse(root);
}
private void postOrderTraverse(Node c) {
if (c == null)
return;
postOrderTraverse(c.left);
postOrderTraverse(c.right);
printlnNode(c);
}
/**
* 层序遍历
*/
public void levelOrderTraverse() {
if (root == null)
return;
Queue<Node> queue = new LinkedList<>();
queue.add(root);
queue.add(null); // 占位符,表示一层结束
while (!queue.isEmpty()) {
Node c = queue.poll();
if (c != null) {
printNode(c);
if (c.left != null)
queue.add(c.left);
if (c.right != null)
queue.add(c.right);
} else {
System.out.println();
if (queue.isEmpty()) // 不加这个判断会死循环
break;
else
queue.add(null); // 占位符,表示一层结束
}
}
}
/**
* 返回二叉树结点个数
* @return 结点个数
*/
public int size() {
return size;
}
private Node findPrevSuccessor(Node n) {
// 转左,然后一路向右
Node s = n.left;
while (s.right != null)
s = s.right;
return s;
}
private void setRoot(Node n) {
root = n;
root.parent = null;
root.isLeft = null;
}
private void resetHolder() {
minSizeNotBalancedTreeRootHolder.key = HOLDER_FLAG_NON;
minSizeNotBalancedTreeRootHolder.left = null;
minSizeNotBalancedTreeRootHolder.right = null;
}
/**
* 对树进行调整,使它保持平衡
*/
private void adjust() {
if (minSizeNotBalancedTreeRootHolder.left != null) {
leftBalance(minSizeNotBalancedTreeRootHolder.left);
} else if (minSizeNotBalancedTreeRootHolder.right != null) {
rightBalance(minSizeNotBalancedTreeRootHolder.right);
}
}
/**
* 左平衡处理,n的左子树高,需要右旋,n的bf=2
* @param n 最小不平衡子树的根结点
*/
private void leftBalance(Node n) {
Node l = n.left;
if (bf(l) == Node.BF_RH) // 新结点插入在n的左孩子的右子树上,n和l的bf符号不同,要作双旋处理
leftRotate(l);
rightRotate(n);
}
/**
* 右平衡处理,n的右子树高,需要左旋,n的bf=-2
* @param n 最小不平衡子树的根结点
*/
private void rightBalance(Node n) {
Node r = n.right;
if (bf(r) == Node.BF_LH) // 新结点插入在n的右孩子的左子树上,n和r的bf符号不同,要作双旋处理
rightRotate(r);
leftRotate(n);
}
/**
* 对子树进行左旋(逆时针旋转)
* @param n 子树的根结点
*/
private void leftRotate(Node n) {
Boolean isLeft = n.isLeft;
Node p = n.parent;
Node r = n.right;
n.right = r.left;
if (n.right != null) {
n.right.parent = n;
n.right.isLeft = Boolean.FALSE;
}
r.left = n;
n.parent = r;
n.isLeft = Boolean.TRUE;
if (p != null) {
if (isLeft) {
p.left = r;
r.isLeft = Boolean.TRUE;
} else
p.right = r;
r.parent = p;
} else
setRoot(r);
}
/**
* 对子树进行右旋(顺时针旋转)
* @param n 子树的根结点
*/
private void rightRotate(Node n) {
Boolean isLeft = n.isLeft;
Node p = n.parent;
Node l = n.left;
n.left = l.right;
if (n.left != null) {
n.left.parent = n;
n.left.isLeft = Boolean.TRUE;
}
l.right = n;
n.parent = l;
n.isLeft = Boolean.FALSE;
if (p != null) {
if (isLeft)
p.left = l;
else {
p.right = l;
p.right.isLeft = Boolean.FALSE;
}
l.parent = p;
} else
setRoot(l);
}
/**
* 求以n为根结点的子树是不是最小不平衡子树
* @param n 结点
*/
private void minSizeNotBalancedTree(Node n) {
if (minSizeNotBalancedTreeRootHolder.key == HOLDER_FLAG_NON) { // 最小不平衡子树还未求出来
minSizeNotBalancedTree1(n);
}
}
private void minSizeNotBalancedTree1(Node n) {
int bf = bf(n);
if (bf >= 2) {
minSizeNotBalancedTreeRootHolder.left = n;
minSizeNotBalancedTreeRootHolder.key = HOLDER_FLAG_HAVE; // 表示已经求出了最小不平衡子树
} else if (bf <= -2) {
minSizeNotBalancedTreeRootHolder.right = n;
minSizeNotBalancedTreeRootHolder.key = HOLDER_FLAG_HAVE; // 表示已经求出了最小不平衡子树
}
}
private void minSizeNotBalancedTree2(Node n) {
while (n != null && minSizeNotBalancedTreeRootHolder.key == HOLDER_FLAG_NON) {
minSizeNotBalancedTree1(n);
n = n.parent;
}
}
public static void main(String[] args) {
//testCase();
//testCase1();
//testCase2();
//testCase3();
testCase4();
}
private static AVLTree initTree() {
int[][] arr = { { 1, 3 }, { 2, 10 }, { 3, 7 }, { 4, 9 }, { 5, 5 }, { 6, 0 }, { 7, 1 }, { 8, 6 }, { 9, 3 }, { 10, 2 } };
AVLTree t = new AVLTree();
for (int[] arr1 : arr) {
t.insert(arr1[0], arr1[1]);
}
return t;
}
private static void testCase() {
AVLTree t = initTree();
System.out.println("tree size: " + t.size());
t.levelOrderTraverse();
}
private static void testCase1() {
AVLTree t = initTree();
System.out.println("tree size: " + t.size());
t.remove(1); // 删除叶子结点
System.out.println("tree size: " + t.size());
t.levelOrderTraverse();
}
private static void testCase2() {
AVLTree t = initTree();
System.out.println("tree size: " + t.size());
t.remove(9); // 删除只有一个孩子的结点
System.out.println("tree size: " + t.size());
t.levelOrderTraverse();
}
private static void testCase3() {
AVLTree t = initTree();
System.out.println("tree size: " + t.size());
t.remove(8); // 删除有两个孩子的结点
System.out.println("tree size: " + t.size());
t.levelOrderTraverse();
}
private static void testCase4() {
AVLTree t = initTree();
System.out.println("key: 4, value: " + t.search(4));
System.out.println("key: 6, value: " + t.search(6));
System.out.println("key: 10, value: " + t.search(10));
System.out.println("key: 12, value: " + t.search(12));
}
}